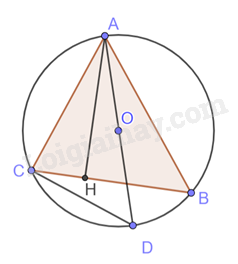
Giải bài tập 12 trang 104 SGK Toán 9 tập 1 - Chân trời sáng tạoCho tam giác ABC có ba đỉnh nằm trên đường tròn (O) và AH là đường cao. Đường thẳng AO cắt đường tròn (O) tại điểm thứ hai D. Chứng minh rằng a) AC vuông góc với DC b) (widehat {ABC} = widehat {ADC}) c) AB. AC = AH. AD Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - KHTN - Lịch sử và Địa lí Đề bài Cho tam giác ABC có ba đỉnh nằm trên đường tròn (O) và AH là đường cao. Đường thẳng AO cắt đường tròn (O) tại điểm thứ hai D. Chứng minh rằng a) AC vuông góc với DC b) ^ABC=^ADCˆABC=ˆADC c) AB. AC = AH. AD Video hướng dẫn giải Phương pháp giải - Xem chi tiết Đọc kĩ dữ liệu để vẽ hình. a) Dựa vào: Góc nội tiếp chắn nửa đường tròn là góc vuông b) Dựa vào: Hai góc nội tiếp cùng chắn một cung thì bằng nhau. c) Chứng minh ΔΔABH ∽ΔADC (g.g) Lời giải chi tiết
a) Ta có ^ACD chắn đường kính AD nên ^ACD=90o. Do đó AC⊥CD b) Ta có ^ABC;^ADC là góc nội tiếp cùng chắn cung AC nên ^ABC=^ADC. c) Tam giác ACD có 3 đỉnh nằm trên đường tròn và AD là đường kính nên tam giác ACD vuông tại C. Suy ra ^AHB=^ACD ^ABC=^ADC (hai góc nội tiếp cùng chắn cung AC) Vậy ΔABH ∽ΔADC (g.g) Do đó, ABAD=AHAC hay AB.AC = AD.AH (đpcm)
>> Học trực tuyến Lớp 9 & Lộ trình UP10 trên Tuyensinh247.com >> Chi tiết khoá học xem: TẠI ĐÂY Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
|