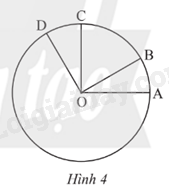
Giải bài tập 11 trang 104 SGK Toán 9 tập 1 - Chân trời sáng tạoQuan sát Hình 4. Biết (widehat {DOA} = {120^o}), OA ( bot )OC, OB ( bot )OD. a) Đọc tên các góc ở tâm có trong hình. b) Tính số đo của mỗi góc ở tâm tìm được ở câu a c) Tìm các cặp cung bằng nhau và có số đo nhỏ hơn 180o d) So sánh hai cung nhỏ (oversetfrown{AB}) và (oversetfrown{CD}). Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - KHTN - Lịch sử và Địa lí Đề bài Quan sát Hình 4. Biết ^DOA=120o, OA ⊥OC, OB ⊥OD. a) Đọc tên các góc ở tâm có trong hình. b) Tính số đo của mỗi góc ở tâm tìm được ở câu a c) Tìm các cặp cung bằng nhau và có số đo nhỏ hơn 180o d) So sánh hai cung nhỏ ⌢AB và ⌢CD.
Video hướng dẫn giải Phương pháp giải - Xem chi tiết Dựa vào: Góc ở tâm là góc có đỉnh trùng với tâm đường tròn, dựa vào hình để xác định góc. Lời giải chi tiết a) Các góc ở tâm có trong hình là: ^DOA;^DOC;^COB;^BOA;^DOB;^COA b) Ta có: ^DOA=120o Vì OA⊥OC nên ^COA=90o Vì OB⊥OD nên ^DOB=90o Từ đó ta tính được: ^DOC=^DOA−^COA=120o−90o=30o ^COB=^DOB−^DOC=90o−30o=60o ^BOA=^COA−^COB=90o−60o=30o c) sđ⌢CD= sđ⌢AB (=30o) sđ⌢BD= sđ⌢AC (=90o) d) sđ⌢AB = sđ⌢CD (=30o)  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
>> Học trực tuyến Lớp 9 & Lộ trình UP10 trên Tuyensinh247.com >> Chi tiết khoá học xem: TẠI ĐÂY Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
|
