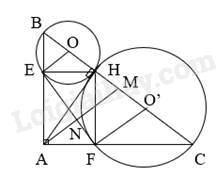
Giải bài tập 11 trang 82 SGK Toán 9 tập 2 - Chân trời sáng tạo

Đề bài

Cho tam giác ABC vuông tại A (AB < AC) có AH là đường cao. Lần lượt vẽ đường tròn (O) đường kính BH và đường tròn (O’) đường kính HC.

a) Xét vị trí tương đối của hai đường tròn (O) và (O’).

b) Đường tròn (O) cắt AB tại E, đường tròn (O’) cắt AC tại F. Chứng minh rằng tứ giác AEHF là hình chữ nhật.

c) Chứng minh rằng EF là tiếp tuyến đường tròn (O) và đồng thời là tiếp tuyến đường tròn (O’).

d) Đường trung tuyến AM của tam giác ABC cắt EF tại N. Cho biết AB = 6 cm, AC = 8 cm. Tính diện tích tam giác ANF.

Lời giải chi tiết

a) Ta có OO’ = OH + O’H = R + R’ suy ra hai đường tròn tiếp xúc nhau.

b) Xét đường tròn (O) có BH là đường kính

$\widehat {BEH}$ là góc nội tiếp chắn nửa đường tròn suy ra $\widehat {BEH}$= 90^o hay AB $\bot$ EH tại E.

Xét đường tròn (O’) có HC là đường kính

$\widehat {HFC}$ là góc nội tiếp chắn nửa đường tròn suy ra $\widehat {HFC}$ = 90^o hay AC $\bot$ HF tại F.

Xét tứ giác AEHF có: 

$\widehat {HEA} = {90^o}$ (chứng minh trên);

$\widehat {EAF} = {90^o}$ (giả thiết);

$\widehat {AFH} = {90^o}$ (chứng minh trên).

Suy ra tứ giác AEHF là hình chữ nhật.

c) Vì OE = OH = R nên $\Delta$OEH cân tại O suy ra $\widehat {OEH} = \widehat {OHE}$.

Ta có $\widehat {BHE} = {90^o} - \widehat B$; $\widehat {BAH} = {90^o} - \widehat B$ suy ra $\widehat {BHE} =$$\widehat {BAH}$.

Mà $\widehat {OEH} = \widehat {BHE}$ (chứng minh trên); $\widehat {BHA} = \widehat {AEF}$ (tính chất hình chữ nhật).

Suy ra $\widehat {OEH} = \widehat {AEF}$ hay $\widehat {OEH} + \widehat {HEF} = \widehat {AEF} + \widehat {HEF}$ suy ra $\widehat {OEF} = \widehat {AEH} = {90^o}$.

Nên EF $\bot$ OE tại E; E $\in$ (O)

Suy ra EF là đường trung tuyến đường tròn (O) (1).

Vì O’F = O’H = R’ nên tam giác O’HF cân tại O’ suy ra $\widehat {O'HF} = \widehat {O'FH}$

Mà $\widehat {AHF} = \widehat {EFH}$ (tính chất hình chữ nhật)

Nên $\widehat {O'HF} + \widehat {AFH} = \widehat {O'HF} + \widehat {EFH}$ hay $\widehat {O'FE} + \widehat {AHC} = {90^o}$.

Nên EF $\bot$ O’F tại F; F $\in$ (O’)

Suy ra EF là đường trung tuyến đường tròn (O’) (2).

Từ (1) và (2) ta có điều phải chứng minh.

d) Tam giác ABC vuông tại A có AM là đường trung tuyến, suy ra ${{AM}} = {{BM}} = {{CM}} = \frac{1}{2}{{BC}}$.

Do đó $\Delta {{AMC}}$ cân tại M , suy ra $\widehat {{{MAC}}} = \widehat {{{MCA}}}$. (1)

Tam giác ${{O}}'{{FC}}$ cân tại ${{O}}'$ (vì ${{O}}'{{F}} = {{O}}'{{C}}$) suy ra $\widehat {{{O}}'{{FC}}} = \widehat {{{O}}'{{CF}}}$.

Suy ra $\widehat {{{MAC}}} = \widehat {{{O}}'{{FC}}}$.

Mà $\widehat {{{MAC}}},\widehat {O'FC}$ là hai góc đồng vị nên ${{AM}}//{{O}}'{{F}}$.

Mặt khác ${{O}}'{{F}} \bot {{EF}}$, suy ra ${{AM}} \bot {{EF}}$ tại N .

Xét tam giác ABC vuông tại A có

${{BC}} = \sqrt {{{A}}{{{B}}^2} + {{A}}{{{C}}^2}}  = \sqrt {{6^2} + {8^2}}  = 10(\;{{cm}})$

Diện tích tam giác ABC là

${{{S}}_{\Delta {{ABC}}}} = \frac{1}{2}{{AH}} \cdot {{BC}} = \frac{1}{2}{{AB}} \cdot {{AC}}$, suy ra ${{AH}} = \frac{{{{AB}} \cdot {{AC}}}}{{{{BC}}}} = \frac{{6 \cdot 8}}{{10}} = 4,8(\;{{cm}})$

Suy ra ${{EF}} = {{AH}} = 4,8\;{{cm}}$ (vì AEHF là hình chữ nhật).

Xét tam giác AHF và tam giác ACH có:

$\widehat {AFH} = \widehat {AHC}\left( { = 90^\circ } \right)$

$\widehat A$ chung

Suy ra $\Delta  \mathrm{AHF} \backsim \Delta  \mathrm{ACH}(\mathrm{g} . \mathrm{g})$ nên $\frac{{{{AH}}}}{{{{AC}}}} = \frac{{{{AF}}}}{{{{AH}}}}$.

Suy ra ${{AF}} = \frac{{{{A}}{{{H}}^2}}}{{{{AC}}}} = \frac{{4,{8^2}}}{8} = 2,88(\;{{cm}})$.

Xét tam giác ANF và tam giác CAB có:

$\widehat {ANF} = \widehat {CAB}\left( { = 90^\circ } \right)$

$\widehat {NAF} = \widehat {ACB}$ (theo (1)

Suy ra $\Delta \text{ANF}\backsim \Delta CAB(\text{g}.\text{g})$

Suy ra $\frac{{{S_{\Delta {{ANF}}}}}}{{{S_{\Delta CAB}}}} = {\left( {\frac{{AF}}{{BC}}} \right)^2}$

Diện tích tam giác AFN là:

${{{S}}_{\Delta AFN}} = {\left( {\frac{{AF}}{{BC}}} \right)^2}.{S_{\Delta CAB}} = {\left( {\frac{{2.88}}{{10}}} \right)^2}.\frac{1}{2}.AB.AC = {\left( {\frac{{2.88}}{{10}}} \right)^2}.\frac{1}{2}.6.8 \approx 2\left( {\;{{c}}{{{m}}^2}} \right)$.