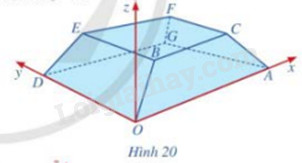
Giải bài tập 11 trang 64 SGK Toán 12 tập 2 - Cánh diều

Đề bài

Hình 20 minh họa hình ảnh một tòa nhà trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục tọa độ là mét). Biết A(50;0;0), D(0;20;0), B(4k;3k;2k) với k > 0 và mặt phẳng (CBEF) có phương trình z = 3

a) Tìm tọa độ điểm B

b) Lập phương trình mặt phẳng (AOBC)

c) Lập phương trình mặt phẳng (DOBE)

d) Chỉ ra một vecto pháp tuyến của mỗi mặt phẳng (AOBC) và (DOBE)

Lời giải chi tiết

a) Ta có \(B \in (CBEF):2k = 3 \Leftrightarrow k = \frac{3}{2}\)

Vậy \(B(6;\frac{9}{2};3)\)

b) \(\overrightarrow {OA}  = (50;0;0);\overrightarrow {OB}  = (6;\frac{9}{2};3)\)

Vecto pháp tuyến của mặt phẳng (AOBC) là: \(\overrightarrow {{n_1}}  = \left[ {\overrightarrow {OA} ;\overrightarrow {OB} } \right] = (0; - 150;225) = 75(0; - 2;3)\)

Phương trình mặt phẳng (AOB) là: -2y + 3z = 0

Vậy phương trình mặt phẳng (AOBC) là -2y + 3z = 0

c) \(\overrightarrow {OD}  = (0;20;0)\)

Vecto pháp tuyến của mặt phẳng (AOBC) là: \(\overrightarrow {{n_2}}  = \left[ {\overrightarrow {OD} ;\overrightarrow {OB} } \right] = (60;0; - 120) = 60(1;0; - 2)\)

Phương trình mặt phẳng (DOB) là: x - 2z = 0

Vậy phương trình mặt phẳng (DOBE) là -2y + 3z = 0

d) Vecto pháp tuyến của mặt phẳng (AOBC) và (DOBE) lần lượt là \(\overrightarrow {{n_1}}  = (0; - 2;3)\)và \(\overrightarrow {{n_2}}  = (1;0; - 2)\)