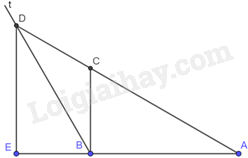
Giải bài tập 10 trang 128 SGK Toán 9 tập 2 - Kết nối tri thứcCho tam giác ABC vuông tại B có góc (widehat A = {30^o},AB = 6cm). Vẽ tia Bt sao cho (widehat {tBC} = {30^o}), cắt tia AC ở D (C nằm giữa A và D). a) Chứng minh tam giác ABD cân tại B. b) Tính khoảng cách từ D đến đường thẳng AB. Tổng hợp Đề thi vào 10 có đáp án và lời giải Toán - Văn - Anh Đề bài Cho tam giác ABC vuông tại B có góc ˆA=30o,AB=6cmˆA=30o,AB=6cm. Vẽ tia Bt sao cho ^tBC=30oˆtBC=30o, cắt tia AC ở D (C nằm giữa A và D). a) Chứng minh tam giác ABD cân tại B. b) Tính khoảng cách từ D đến đường thẳng AB. Video hướng dẫn giải Phương pháp giải - Xem chi tiết a) + Tính được ^DBA=^DBC+^CBA=120oˆDBA=ˆDBC+ˆCBA=120o. + Tính được ^BDA=30oˆBDA=30o nên tam giác ABD cân tại B. b) + BD=AB=6cmBD=AB=6cm. + Kẻ DE vuông góc với AB tại E. Khi đó, DE là khoảng cách từ D đến đường thẳng AB. + ^DBE=180o−^DBA=60oˆDBE=180o−ˆDBA=60o. + Tam giác BED vuông tại E nên ED=BD.sin^DBEED=BD.sinˆDBE. Lời giải chi tiết
a) ΔΔABC vuông tại B nên ^CBA=90oˆCBA=90o. Ta có: ^DBA=^DBC+^CBA=30o+90o=120oˆDBA=ˆDBC+ˆCBA=30o+90o=120o ΔΔDBA có: ^BDA=180o−^DBA−ˆA=180o−120o−30o=30oˆBDA=180o−ˆDBA−ˆA=180o−120o−30o=30o. Do đó, ^BDA=ˆAˆBDA=ˆA nên ΔΔABD cân tại B. b) Vì ΔΔABD cân tại B nên BD=AB=6cmBD=AB=6cm. Kẻ DE vuông góc với AB tại E. Khi đó, DE là khoảng cách từ D đến đường thẳng AB. Ta có: ^DBE=180o−^DBA=180o−120o=60oˆDBE=180o−ˆDBA=180o−120o=60o. ΔΔBED vuông tại E nên ED=BD.sin^DBE=6.sin60o=6.√32=3√3(cm)ED=BD.sinˆDBE=6.sin60o=6.√32=3√3(cm) Vậy khoảng cách từ D đến đường thẳng AB bằng 3√33√3cm.  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
|
