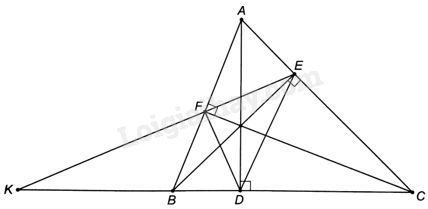
Giải bài 9.52 trang 62 sách bài tập toán 9 - Kết nối tri thức tập 2

Đề bài

Cho tam giác nhọn ABC (AB<AC) có các đường cao AD, BE, CF. Cho EF cắt BC tại K. Chứng minh rằng:

a) KB. KC = KE. KF;

b) $\frac{{KB}}{{KC}} = \frac{{DB}}{{DC}}$.

Lời giải chi tiết

a) Vì $\widehat {BFC} = \widehat {BEC} = {90^o}$ nên tứ giác BFEC nội tiếp đường tròn đường kính BC.

Chứng minh tương tự ta có: tứ giác AFDC nội tiếp đường tròn đường kính AC, tứ giác AEDB nội tiếp đường tròn đường kính AB.

Vì tứ giác BFEC nội tiếp đường tròn đường kính BC nên $\widehat {KFB} = {180^o} - \widehat {BFE} = \widehat {BCE}$.

Tam giác KFB và tam giác KCE có: $\widehat {KFB} = \widehat {BCE}$, góc K chung.

Suy ra: $\Delta KFB\backsim \Delta KCE\left( g.g \right)$. Suy ra, $\frac{{KF}}{{KC}} = \frac{{KB}}{{KE}}$, hay KB. KC = KE. KF.

b) Hai tam giác KEB và tam giác KCF có: $\widehat {KEB} = \widehat {KCF}$ (hai góc nội tiếp cùng chắn cung BF của đường tròn đường kính BC), góc K chung nên $\Delta KEB\backsim \Delta KCF\left( g.g \right)$, suy ra $\frac{{KE}}{{KC}} = \frac{{EB}}{{CF}}$.

Mặt khác: $\frac{{KB}}{{KE}} = \frac{{FB}}{{CE}}$ (do $\Delta KFB\backsim \Delta KCE\left( cmt \right)$). Suy ra: $\frac{{KB}}{{KC}} = \frac{{KB}}{{KE}}.\frac{{KE}}{{KC}} = \frac{{BF}}{{CF}}.\frac{{BE}}{{CE}}$ (1)

Chứng minh tương tự ta có: hai tam giác BDF và tam giác BAC có:

$\widehat {BDF} = {180^o} - \widehat {FDC} = \widehat {BAC};\widehat {DBF} = \widehat {ABC}$.

Suy ra: $\Delta BDF\backsim \Delta BAC\left( g.g \right)$, suy ra $\frac{{DB}}{{AB}} = \frac{{BF}}{{BC}}$. Tương tự ta có: $\frac{{DC}}{{AC}} = \frac{{CE}}{{BC}}$ nên $\frac{{DB}}{{DC}} = \frac{{BF}}{{CE}}.\frac{{AB}}{{AC}}$ (2)

Mà $\Delta ABE\backsim \Delta ACF$ (hai tam giác vuông có chung góc nhọn BAC). Do đó, $\frac{{AB}}{{AC}} = \frac{{BE}}{{CF}}$ (3).

Từ (1), (2) và (3) ta có: $\frac{{KB}}{{KC}} = \frac{{DB}}{{DC}}$.