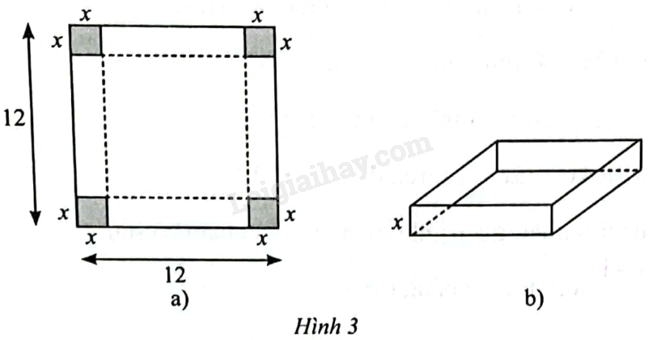
SBT Toán 12 - giải SBT Toán 12 - Chân trời sáng tạo

Giải bài 8 trang 18 sách bài tập toán 12 - Chân trời sáng tạo

Từ một miếng bìa hình vuông có cạnh bằng 12 cm, người ta cắt bỏ đi bốn hình vuông nhỏ có cạnh bằng (x) (cm) ở bốn góc (Hình 3a) và gấp lại thành một hình hộp không nắp (Hình 3b). Tìm (x) để thể tích của hình hộp là lớn nhất.

Tổng hợp đề thi học kì 2 lớp 12 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Hoá - Sinh - Sử - Địa

Đề bài

Từ một miếng bìa hình vuông có cạnh bằng 12 cm, người ta cắt bỏ đi bốn hình vuông nhỏ có cạnh bằng $x$ (cm) ở bốn góc (Hình 3a) và gấp lại thành một hình hộp không nắp (Hình 3b). Tìm $x$ để thể tích của hình hộp là lớn nhất.

Phương pháp giải - Xem chi tiết

Sử dụng công thức tính thể tích hình hộp chữ nhật để tính thể tích $V\left( x \right)$ , sau đó tìm giá trị lớn nhất của hàm số $V\left( x \right)$ .

Quảng cáo

Lời giải chi tiết

Theo đề bài ta có: Cạnh của hộp là: $12 - 2{\rm{x}}\left( {cm} \right)$ .

Chiều cao của hộp là: ${\rm{x}}\left( {cm} \right)$ .

Thể tích của hộp là: $V\left( x \right) = x{\left( {12 - 2{\rm{x}}} \right)^2} = 4{{\rm{x}}^3} - 48{{\rm{x}}^2} + 144{\rm{x}}\left( {c{m^3}} \right)$ .

Vì cạnh của hộp không âm nên $12 - 2{\rm{x}} \ge 0 \Leftrightarrow x \le 6$

Xét hàm số $V\left( x \right) = 4{{\rm{x}}^3} - 48{{\rm{x}}^2} + 144{\rm{x}}$ trên đoạn $\left[ {0;6} \right]$ .

Ta có: $V'\left( x \right) = 12{{\rm{x}}^2} - 96{\rm{x}} + 144$

$V'\left( x \right) = 0 \Leftrightarrow x = 6$ hoặc $x = 2$ .

$V\left( 0 \right) = 0;V\left( 2 \right) = 128;V\left( 6 \right) = 0$

Vậy $\mathop {\max }\limits_{\left[ {0;6} \right]} V\left( x \right) = V\left( 2 \right) = 128$ .

Vậy với $x = 2\left( {cm} \right)$ thì thể tích của hình hộp là lớn nhất.

Chia sẻ

Bình luận

Bình chọn:

4.9 trên 7 phiếu

Giải bài 9 trang 18 sách bài tập toán 12 - Chân trời sáng tạo
Cho tam giác (ABC) cân tại (A) nội tiếp trong đường tròn tâm (O), bán kính 1 cm. Đặt (widehat A = alpha left( {0 < alpha < pi } right)). a) Viết biểu thức tính diện tích (S) của tam giác (ABC) theo (alpha ). b) Tìm diện tích lớn nhất của tam giác (ABC).
Giải bài 10 trang 18 sách bài tập toán 12 - Chân trời sáng tạo
Cho hình thang cân có đáy nhỏ và hai cạnh bên bằng nhau và bằng 5. Tìm diện tích lớn nhất của hình thang cân đó.
Giải bài 11 trang 18 sách bài tập toán 12 - Chân trời sáng tạo
Trong một ngày, tổng chi phí để một xưởng sản xuất $x$ (kg) thành phẩm được cho bởi hàm số $C\left( x \right) = 2{x^3} - 30{x^2} + 177x + 2592$ (nghìn đồng). Biết giá bán mỗi kilôgam thành phẩm là 513 nghìn đồng và công suất tối đa của xưởng là 20 kg trong một ngày. Khối lượng thành phẩm xưởng nên sản xuất trong một ngày là bao nhiêu để lợi nhuận thu được của xưởng trong một ngày là cao nhất?
Giải bài 12 trang 18 sách bài tập toán 12 - Chân trời sáng tạo
Giá bán $P$ (đồng) của một sản phẩm thay đổi theo số lượng $Q$ sản phẩm $\left( {0 \le Q \le 1500} \right)$ được cung cấp ra thị trường theo công thức $P = \sqrt {1500 - Q}$ . Tính số lượng sản phẩm nên được cung cấp ra thị trường để doanh thu $R = PQ$ lớn nhất.
Giải bài 7 trang 17 sách bài tập toán 12 - Chân trời sáng tạo
Cho $a$ và $b$ là hai số không âm và có tổng bằng 4. Tìm giá trị nhỏ nhất của ${a^4} + {b^4}$ .

Luyện Bài Tập Trắc nghiệm Toán 12 - Chân trời sáng tạo - Xem ngay

Báo lỗi - Góp ý

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.