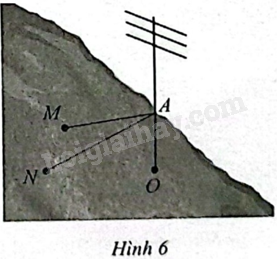
Giải bài 7 trang 55 sách bài tập toán 12 - Chân trời sáng tạo

Đề bài

Người ta muốn dựng một cột ăng-ten trên một sườn đồi. Ăng-ten được dựng thẳng đứng trong không gian $Oxyz$ với độ dài đơn vị trên mỗi trục bằng 1 m. Gọi $O$ là gốc cột, $A$ là điểm buộc dây cáp vào cột ăng-ten và $M,N$ là hai điểm neo dây cáp xuống mặt sườn đồi (Hình 6). Cho biết toạ độ các điểm nói trên lần lượt là $O\left( {0;0;0} \right),A\left( {0;0;6} \right),M\left( {3; - 4;3} \right),$$N\left( { - 5; - 2;2} \right)$.

a) Tính độ dài các đoạn dây cáp $MA$ và $NA$.

b) Tính góc tạo bởi các sợi dây cáp $MA,NA$ với mặt phẳng sườn đồi.

Lời giải chi tiết

a) Ta có: $MA = \left| {\overrightarrow {MA} } \right| = \sqrt {{{\left( {0 - 4} \right)}^2} + {{\left( {0 - \left( { - 4} \right)} \right)}^2} + {{\left( {6 - 3} \right)}^2}}  = \sqrt {34}  \approx 5,8\left( m \right)$.

$NA = \left| {\overrightarrow {NA} } \right| = \sqrt {{{\left( {0 - \left( { - 5} \right)} \right)}^2} + {{\left( {0 - \left( { - 2} \right)} \right)}^2} + {{\left( {6 - 2} \right)}^2}}  = \sqrt {45}  \approx 6,7\left( m \right)$.

b) Ta có: $\overrightarrow {MA}  = \left( { - 3;4;3} \right),\overrightarrow {NA}  = \left( {5;2;4} \right),\overrightarrow {OM}  = \left( {3; - 4;3} \right),\overrightarrow {ON}  = \left( { - 5; - 2;2} \right)$

$\left[ {\overrightarrow {OM} ,\overrightarrow {ON} } \right] = \left( { - 2; - 21; - 26} \right)$.

Do đó $\left( {OMN} \right)$ có vectơ pháp tuyến $\overrightarrow n  = \left( { - 2; - 21; - 26} \right)$.

Ta có:

$\sin \left( {MA,\left( {OMN} \right)} \right) = \left| {\cos \left( {\overrightarrow {MA} ,\overrightarrow n } \right)} \right| = \frac{{\left| {\left( { - 3} \right).\left( { - 2} \right) + 4.\left( { - 21} \right) + 3.\left( { - 26} \right)} \right|}}{{\sqrt {{{\left( { - 3} \right)}^2} + {4^2} + {3^2}} .\sqrt {{{\left( { - 2} \right)}^2} + {{\left( { - 21} \right)}^2} + {{\left( { - 26} \right)}^2}} }} = \frac{{156}}{{\sqrt {38114} }}$

Vậy $\left( {MA,\left( {OMN} \right)} \right) \approx {53^ \circ }$.

$\sin \left( {NA,\left( {OMN} \right)} \right) = \left| {\cos \left( {\overrightarrow {NA} ,\overrightarrow n } \right)} \right| = \frac{{\left| {5.\left( { - 2} \right) + 2.\left( { - 21} \right) + 4.\left( { - 26} \right)} \right|}}{{\sqrt {{5^2} + {2^2} + {4^2}} .\sqrt {{{\left( { - 2} \right)}^2} + {{\left( { - 21} \right)}^2} + {{\left( { - 26} \right)}^2}} }} = \frac{{156}}{{\sqrt {50445} }}$

Vậy $\left( {NA,\left( {OMN} \right)} \right) \approx {44^ \circ }$.