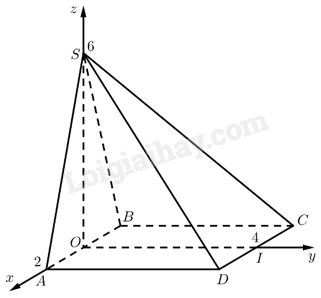
Giải bài 6 trang 55 sách bài tập toán 12 - Chân trời sáng tạo

Đề bài

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh bằng 4. Mặt bên $SAB$ là tam giác cân tại $S$ có chiều cao bằng 6 và nằm trong mặt phẳng vuông góc với đáy.

a) Tính góc $\alpha$ giữa hai đường thẳng $SD$ và $BC$;

b) Tính góc $\beta$ giữa hai mặt phẳng $\left( {SAD} \right)$ và $\left( {SCD} \right)$.

Lời giải chi tiết

Gọi $O$ là trung điểm của $AB$, $I$ là trung điểm của $C{\rm{D}}$.

$SAB$ là tam giác cân tại $S$ nên $SO \bot AB$, suy ra $SO \bot \left( {ABCD} \right)$.

Chọn hệ trục $Oxyz$ như hình vẽ. Ta có:

$S\left( {0;0;6} \right),A\left( {2;0;0} \right),B\left( { - 2;0;0} \right),C\left( { - 2;4;0} \right),D\left( {2;4;0} \right)$.

a) Ta có $\overrightarrow {SD}  = \left( {2;4; - 6} \right),\overrightarrow {BC}  = \left( {0;4;0} \right)$, suy ra

$\cos \left( {S{\rm{D}},BC} \right) = \left| {\cos \left( {\overrightarrow {S{\rm{D}}} ,\overrightarrow {BC} } \right)} \right| = \frac{{\left| {2.0 + 4.4 + \left( { - 6} \right).0} \right|}}{{\sqrt {{2^2} + {4^2} + {{\left( { - 6} \right)}^2}} .\sqrt {{0^2} + {4^2} + {0^2}} }} = \frac{{\sqrt {14} }}{7}$

Vậy $\left( {S{\rm{D}},BC} \right) \approx {57,7^ \circ }$.

b) Ta có: $\overrightarrow {SD}  = \left( {2;4; - 6} \right),\overrightarrow {SA}  = \left( {2;0; - 6} \right) \Rightarrow \left[ {\overrightarrow {SD} ,\overrightarrow {SA} } \right] = \left( { - 24;0; - 8} \right) =  - 8\left( {3;0;1} \right)$.

Do đó $\left( {SAD} \right)$ có vectơ pháp tuyến $\overrightarrow n  = \left( {3;0;1} \right)$.

$\overrightarrow {SD}  = \left( {2;4; - 6} \right),\overrightarrow {CD}  = \left( {4;0;0} \right) \Rightarrow \left[ {\overrightarrow {SD} ,\overrightarrow {CD} } \right] = \left( {0; - 24; - 16} \right) =  - 8\left( {0;3;2} \right)$.

Do đó $\left( {SCD} \right)$ có vectơ pháp tuyến $\overrightarrow {n'}  = \left( {0;3;2} \right)$.

$\cos \left( {\left( {SAD} \right),\left( {SCD} \right)} \right) = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n'} } \right)} \right| = \frac{{\left| {3.0 + 0.3 + 1.2} \right|}}{{\sqrt {{3^2} + {0^2} + {1^2}} .\sqrt {{0^2} + {3^2} + {2^2}} }} = \frac{{2\sqrt {130} }}{{130}}$

Vậy $\left( {\left( {SAD} \right),\left( {SCD} \right)} \right) \approx {79,9^ \circ }$.