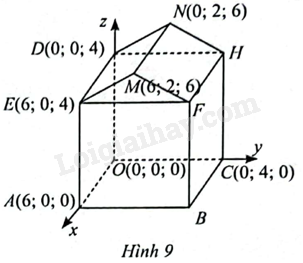
Giải bài 7 trang 46 sách bài tập toán 12 - Chân trời sáng tạoMột kĩ sư xây dựng thiết kế khung một ngôi nhà trong không gian (Oxyz) như Hình 9 nhờ một phần mềm đồ hoạ máy tính. a) Viết phương trình mặt phẳng mái nhà (left( {DEMM} right)). b) Tính khoảng cách từ điểm (B) đến mái nhà (left( {DEMM} right)). Đề bài Một kĩ sư xây dựng thiết kế khung một ngôi nhà trong không gian \(Oxyz\) như Hình 9 nhờ một phần mềm đồ hoạ máy tính.
a) Viết phương trình mặt phẳng mái nhà \(\left( {DEMM} \right)\). b) Tính khoảng cách từ điểm \(B\) đến mái nhà \(\left( {DEMM} \right)\). Phương pháp giải - Xem chi tiết Lập phương trình tổng quát của mặt phẳng đi qua ba điểm không thẳng hàng \(A,B,C\): Bước 1: Tìm cặp vectơ chỉ phương, chẳng hạn \(\overrightarrow {AB} ,\overrightarrow {AC} \). Bước 2: Tìm một vectơ pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\). Bước 3: Viết phương trình mặt phẳng \(\left( \alpha \right)\) đi qua điểm \(A\) và có vectơ pháp tuyến \(\overrightarrow n \). ‒ Khoảng cách từ điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) đến mặt phẳng \(\left( P \right):Ax + By + C{\rm{z}} + D = 0\): $d\left( {{M}_{0}};\left( P \right) \right)=\frac{\left| A{{x}_{0}}+B{{y}_{0}}+C{{\text{z}}_{0}}+D \right|}{\sqrt{{{A}^{2}}+{{B}^{2}}+{{C}^{2}}}}$. Lời giải chi tiết a) Ta có: \(\overrightarrow {DE} = \left( {6;0;0} \right),\overrightarrow {DN} = \left( {0;2;2} \right)\). Khi đó, \(\left[ {\overrightarrow {DE} ,\overrightarrow {DN} } \right] = \left( {0.2 - 0.2;0.0 - 6.2;6.2 - 0.0} \right) = \left( {0; - 12;12} \right)\) là vectơ pháp tuyến của mặt phẳng \(\left( {DEMM} \right)\). Phương trình mặt phẳng \(\left( {DEMM} \right)\) là: \(0\left( {x - 0} \right) - 12\left( {y - 0} \right) + 12\left( {z - 4} \right) = 0 \Leftrightarrow - 12y + 12{\rm{z}} - 48 = 0 \Leftrightarrow y - z + 4 = 0\). b) \(OABC.DEFH\) là hình hộp chữ nhật nên \(B\left( {6;4;0} \right)\) Khoảng cách từ điểm \(B\) đến mái nhà \(\left( {DEMM} \right)\) bằng: \(d\left( {B,\left( {DEMM} \right)} \right) = \frac{{\left| {4 - 0 + 4} \right|}}{{\sqrt {{0^2} + {1^2} + {{\left( { - 1} \right)}^2}} }} = 4\sqrt 2 \).  Chia sẻ Bình luận
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
