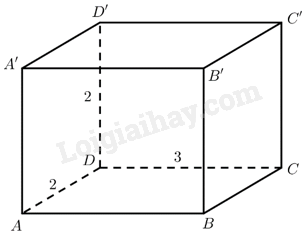
Giải bài 6 trang 46 sách bài tập toán 12 - Chân trời sáng tạo

Đề bài

Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(DA = 2,DC = 3,DD = 2\).

Tính khoảng cách từ đỉnh \(B'\) đến mặt phẳng \(\left( {BA'C'} \right)\).

Lời giải chi tiết

Vì \(ABCD.A'B'C'D'\) là hình hộp chữ nhật nên các đường thẳng \(DA,DC,DD'\) đôi một vuông góc.

Do đó ta có thể gắn hệ trục toạ độ \(Oxyz\) thoả mãn \(D\left( {0;0;0} \right),A\left( {2;0;0} \right),C\left( {0;3;0} \right),D'\left( {0;0;2} \right)\).

Khi đó \(B\left( {2;3;0} \right),B'\left( {2;3;2} \right),A'\left( {2;0;2} \right),C'\left( {0;3;2} \right)\).

Ta có: \(\overrightarrow {BA'}  = \left( {0; - 3;2} \right),\overrightarrow {BC'}  = \left( { - 2;0;2} \right)\).

Khi đó, \(\left[ {\overrightarrow {BA'} ,\overrightarrow {BC'} } \right] = \left( {\left( { - 3} \right).2 - 2.0;2.\left( { - 2} \right) - 0.2;0.0 - \left( { - 3} \right).\left( { - 2} \right)} \right) = \left( { - 6; - 4; - 6} \right)\) là vectơ pháp tuyến của mặt phẳng \(\left( {BA'C'} \right)\).

Phương trình mặt phẳng \(\left( {BA'C'} \right)\) là:

\( - 6\left( {x - 2} \right) - 4\left( {y - 3} \right) - 6\left( {z - 0} \right) = 0 \Leftrightarrow  - 6x - 4y - 6{\rm{z}} + 24 = 0 \Leftrightarrow 3{\rm{x}} + 2y + 3{\rm{z}} - 12 = 0\).

Khi đó khoảng cách từ điểm \(B'\) đến mặt phẳng \(\left( {BA'C'} \right)\) bằng:

\(d\left( {B',\left( {BA'C'} \right)} \right) = \frac{{\left| {3.2 + 2.3 + 3.2 - 12} \right|}}{{\sqrt {{3^2} + {2^2} + {3^2}} }} = \frac{{3\sqrt {22} }}{{11}}\).