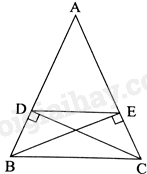
Giải bài 6 trang 60 sách bài tập toán 8 - Chân trời sáng tạo

Đề bài

Cho tam giác ABC cân tại A, có hai đường cao BE và CD \(\left( {D \in AB,E \in AC} \right)\). Chứng minh tứ giác BDEC là hình thang cân.

Lời giải chi tiết

Vì tam giác ABC cân tại A nên \(AB = AC\) và \(\widehat {ABC} = \widehat {ACB}\)

Mà \(\widehat {ABC} + \widehat {ACB} + \widehat A = {180^0}\) nên \(\widehat {ABC} = \frac{{{{180}^0} - \widehat A}}{2}\) (1)

Tam giác AEB và tam giác ADC có:

\(\widehat {ADC} = \widehat {AEB} = {90^0},AB = AC,\widehat A\;chung\)

Do đó, \(\Delta AEB = \Delta ADC\left( {ch - gn} \right)\). Suy ra \(AD = AE\)

Do đó, tam giác AED cân tại E. Suy ra: \(\widehat {ADE} = \widehat {AED}\)

Mà \(\widehat {ADE} + \widehat {AED} + \widehat A = {180^0}\) nên \(\widehat {ADE} = \frac{{{{180}^0} - \widehat A}}{2}\) (2)

Từ (1) và (2) ta có: \(\widehat {ABC} = \widehat {ADE}\)

Mà hai góc này ở vị trí đồng vị nên DE//BC

Do đó, tứ giác BDEC là hình thang

Lại có: \(\widehat {DBC} = \widehat {ECB}\) (cmt) nên tứ giác BDEC là hình thang cân