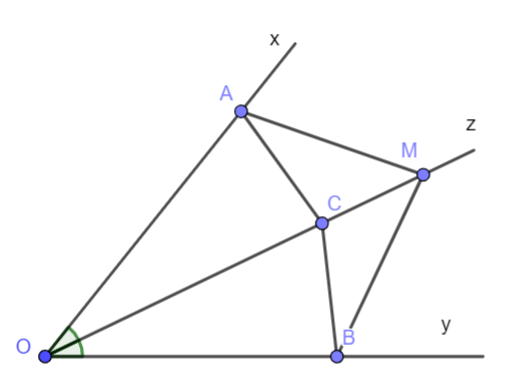
Giải bài 4 (4.19) trang 67 vở thực hành Toán 7Bài 4 (4.19). Cho tia Oz là phân giác của góc xOy. Lấy các điểm A, B, C lần lượt thuộc các tia Ox, Oy, Oz sao cho \(\widehat {CAO} = \widehat {CBO}\) a) Chứng minh rằng \(\Delta OAC = \Delta OBC\) b) Lấy điểm M trên tia đối của tia CO. Chứng minh rằng \(\Delta MAC = \Delta MBC\) Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên... Đề bài Bài 4 (4.19). Cho tia Oz là phân giác của góc xOy. Lấy các điểm A, B, C lần lượt thuộc các tia Ox, Oy, Oz sao cho \(\widehat {CAO} = \widehat {CBO}\) a) Chứng minh rằng \(\Delta OAC = \Delta OBC\) b) Lấy điểm M trên tia đối của tia CO. Chứng minh rằng \(\Delta MAC = \Delta MBC\) Phương pháp giải - Xem chi tiết Chứng minh hai tam giác bằng nhau theo trường hợp g – c – g Lời giải chi tiết
a) Xét hai tam giác OAC và OBC ta có \(\widehat {COA} = \widehat {COB}\)(OC là tia phân giác của góc AOB) OC là cạnh chung \(\widehat {ACO} = {180^o} - \widehat {CAO} - \widehat {COA} = {180^o} - \widehat {CBO} - \widehat {COB} = \widehat {BCO}\) Vậy \(\Delta OAC = \Delta OBC\)(g – c – g ) b) Xét hai tam giác MAC và MBC ta có CA = CB ( do \(\Delta OAC = \Delta OBC\)) \(\widehat {MCA} = {180^o} - \widehat {OCA} = {180^o} - \widehat {OCB} = \widehat {MCB}\)( do \(\Delta OAC = \Delta OBC\)) MC là cạnh chung Vậy \(\Delta MAC = \Delta MBC\)(c – g – c )
|