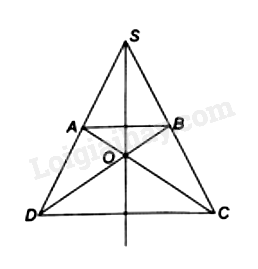
Giải bài 3.10 trang 34 sách bài tập toán 8 - Kết nối tri thức với cuộc sống

Đề bài

Cho hình thang cân ABCD với hai đường thẳng chứa hai cạnh bên AD, BC cắt nhau tại S. Gọi O là giao điểm của hai đường chéo AC và BD. Chứng minh đường thẳng SO đi qua trung điểm của AB, đi qua trung điểm của CD.

Lời giải chi tiết

Do ABCD là hình thang cân nên AD = BC, AC = BD, $\widehat {ADC} = \widehat {BCD}$

Xét $\Delta ABC$ và $\Delta BAD$ có

$BC = AD,AC = BD$

Cạnh AB chung

Do đó $\Delta ABC = \Delta BAD$ (c.c.c)

Suy ra $\widehat {BAC} = \widehat {ABD}$.

Từ đó $\Delta OAB$ là tam giác cân tại O, nên $OA = OB.$

Ta có: $OA + OC = AC$;$OB + OD = BD$ , mà $OA = OB,AC = BD$

Suy ra $OC = OD$

Do đó O cách đều A và B; O cách đều C và D;

Do $AB//CD$ nên $\widehat {SAB} = \widehat {SDC}$; $\widehat {SBA} = \widehat {SCD}$ (các cặp góc ở vị trí đồng vị)

Mà $\widehat {ADC} = \widehat {BCD}$ hay $\widehat {SDC} = \widehat {SCD}$

 suy ra $\widehat {SAB} = \widehat {SDC} = \widehat {SBA} = \widehat {SCD}$.

Suy ra là $\Delta SAB$, $\Delta SCD$ các tam giác cân tại đỉnh S nên $SA = SB,SC = SD$

Do đó S cũng cách đều A và B, cách đều C và D.

Vậy S và O cùng nằm trên đường trung trực của AB, của CD nên đường thẳng SO đi qua trung điểm của AB, CD.