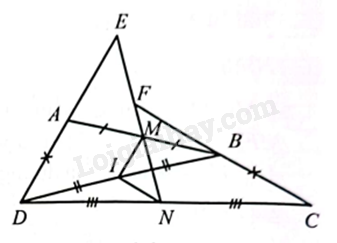
Giải bài 19 trang 66 sách bài tập toán 8 – Cánh diều

Đề bài

Cho tứ giác $ABCD$ có $AD = BC$. Đường thẳng đi qua trung điểm $M$ và $N$ lần lượt của các cạnh $AB$ và $CD$ cắt các đường thẳng $AD$ và $BC$ lần lượt tại $E$ và $F$. Chứng minh: $\widehat {AEM} = \widehat {MFB}$.

Lời giải chi tiết

Lấy $I$ là trung điểm của $BD$. Do $MI.NI$ lần lượt là các đường trung bình của tam giác $ABD$ và $BDC$ nên $MI = \frac{{AD}}{2}$, $MI//AD,NI = \frac{{BC}}{2};NI//BC$. Mà $AD = BC$ nên $MI = NI$, suy ra tam giác $IMN$ cân ở $I$.

Do đó $\widehat {IMN} = \widehat {INM}$. Lại có $\widehat {IMN} = \widehat {AEM}$ (hai góc đồng vị, $IM//AE$). Suy ra $\widehat {INM} = \widehat {AEM}$. Mặt khác $\widehat {INM} = \widehat {MDB}$ (hai góc so le trong, $IN//FB$). Suy ra $\widehat {AEM} = \widehat {MFB}$.