Đề thi học kì 1 Toán 8 Chân trời sáng tạo - Đề số 8Tổng hợp đề thi học kì 2 lớp 8 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Khoa học tự nhiên Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:Đề bài
I. Trắc nghiệm
Chọn câu trả lời đúng trong mỗi câu sau:
Câu 1 :
Trong các biểu thức sau, biểu thức nào không phải là đa thức?
Câu 2 :
Dùng hằng đẳng thức đáng nhớ biến đổi biểu thức \({\left( {x - 2y} \right)^2}\) ta được kết quả là:
Câu 3 :
Điều kiện xác định của phân thức \(\frac{{3x}}{{x - 2}}\) là:
Câu 5 :
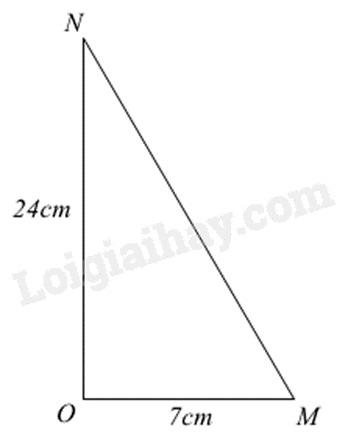
Tam giác OMN vuông tại O có OM = 7cm, ON = 24cm thì độ dài cạnh MN là:
Câu 8 :
Biểu đồ nào thích hợp để biểu diễn tỉ lệ phần trăm số huy chương vàng của mỗi đoàn so với tổng số huy chương vàng đã trao trong đại hội?
Câu 9 :
Kết quả của phép nhân \(2{x^5}.\left( {3x - 2{x^2}} \right)\) là:
Câu 10 :
Hình chóp tam giác đều có cạnh đáy là 4 cm và chiều cao của mặt bên tương ứng với cạnh đáy là 3 cm có diện tích xung quanh là:
Câu 11 :
Phát biểu nào sau đây sai?
Câu 12 :
Bộ ba số đo nào sau đây là độ dài ba cạnh của một tam giác vuông?
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Chọn câu trả lời đúng trong mỗi câu sau:
Câu 1 :
Trong các biểu thức sau, biểu thức nào không phải là đa thức?
Đáp án : C Phương pháp giải :
+ Đa thức nhiều biến (hay đa thức) là một tổng của những đơn thức. + Mỗi đơn thức được gọi là một đa thức (chỉ chứa một hạng tử). Lời giải chi tiết :
Biểu thức \(\frac{1}{{xy}}\) không phải là đa thức. Đáp án C
Câu 2 :
Dùng hằng đẳng thức đáng nhớ biến đổi biểu thức \({\left( {x - 2y} \right)^2}\) ta được kết quả là:
Đáp án : C Phương pháp giải :
Sử dụng hằng đẳng thức bình phương của một hiệu: \({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\). Lời giải chi tiết :
Ta có: \({\left( {x - 2y} \right)^2} = {x^2} - 4xy + 4{y^2}\). Đáp án C
Câu 3 :
Điều kiện xác định của phân thức \(\frac{{3x}}{{x - 2}}\) là:
Đáp án : B Phương pháp giải :
Phân thức xác định khi mẫu thức khác 0. Lời giải chi tiết :
Phân thức \(\frac{{3x}}{{x - 2}}\) xác định khi \(x - 2 \ne 0\), suy ra \(x \ne 2\). Đáp án B
Đáp án : C Phương pháp giải :
Hình chóp tứ giác đều là hình có một đỉnh và đáy là hình vuông. Lời giải chi tiết :
Hình 3 biểu diễn hình chóp tứ giác đều. Đáp án C
Câu 5 :
Tam giác OMN vuông tại O có OM = 7cm, ON = 24cm thì độ dài cạnh MN là:
Đáp án : D Phương pháp giải :
Áp dụng định lí Pythagore trong tam giác vuông: bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông. Lời giải chi tiết :
Áp dụng định lí Pythagore vào tam giác OMN vuông tại O, ta có: \(M{N^2} = O{M^2} + O{N^2} = {7^2} + {24^2} = 625\) Suy ra \(MN = \sqrt {625} = 25\) Đáp án D
Đáp án : C Phương pháp giải :
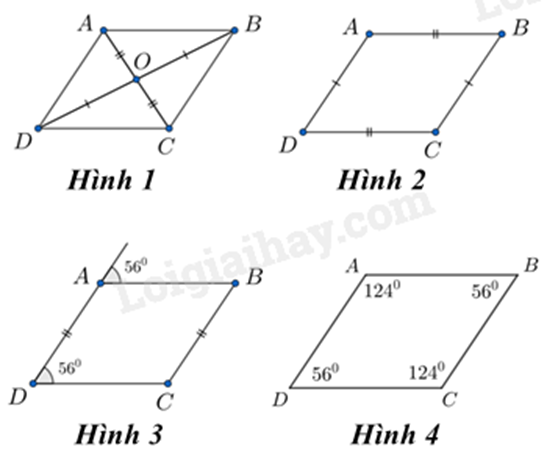
Dựa vào các dấu hiệu nhận biết hình bình hành: - Tứ giác có các cạnh đối bằng nhau là một hình bình hành. - Tứ giác có một cặp cạnh đối song song và bằng nhau là một hình bình hành. - Tứ giác có các góc đối bằng nhau là một hình bình hành. - Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là một hình bình hành. Lời giải chi tiết :
- Hình 1 là tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là một hình bình hành. - Hình 2 là tứ giác có các cạnh đối bằng nhau là một hình bình hành. - Hình 4 là tứ giác có các góc đối bằng nhau là một hình bình hành. Vậy ta chọn hình 3. Đáp án C
Đáp án : B Phương pháp giải :
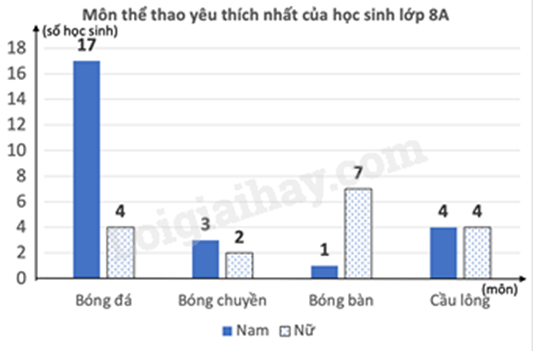
Quan sát biểu đồ để xác định số học sinh yêu thích các môn thể thao. Lời giải chi tiết :
Quan sát biểu đồ, ta thấy: - Số học sinh nam yêu thích nhất môn Bóng đá là 17 học sinh nên A sai. - Số học sinh yêu thích nhất môn Bóng chuyền là 3 + 2 = 5 học sinh nên B đúng. - Số học sinh nữ yêu thích nhất môn Bóng bàn là 7 học sinh nên C sai. - Số học sinh nam yêu thích nhất môn Cầu lông là 4 học sinh nên D sai. Đáp án B
Câu 8 :
Biểu đồ nào thích hợp để biểu diễn tỉ lệ phần trăm số huy chương vàng của mỗi đoàn so với tổng số huy chương vàng đã trao trong đại hội?
Đáp án : A Phương pháp giải :
Dựa vào mục đích biểu diễn của các loại biểu đồ để lựa chọn biểu đồ thích hợp. Biểu đồ tranh: Tạo sự lôi cuốn, thu hút bằng hình ảnh. Biểu đồ cột: Sử dụng các chiều cao của các hình chữ nhật để biểu diễn số liệu. Thuận tiện trong việc so sánh. Biểu đồ đoạn thẳng: Biểu diễn sự thay đổi số liệu của đối tượng theo thời gian. Biểu đồ cột kép: So sánh một cách trực quan từng cặp số liệu của hai bộ dữ liệu cùng loại. Biểu đồ hình quạt tròn: Biểu thị tỉ lệ phần trăm từng loại số liệu so với toàn thể. Lời giải chi tiết :
Biểu diễn tỉ lệ phần trăm số huy chương vàng của mỗi đoàn so với tổng số huy chương vàng là biểu thị tỉ lệ phần trăm từng loại so với toàn thể thên ta chọn biểu đồ hình quạt tròn. Đáp án A
Câu 9 :
Kết quả của phép nhân \(2{x^5}.\left( {3x - 2{x^2}} \right)\) là:
Đáp án : B Phương pháp giải :
Để thực hiện nhân đơn thức với đa thức, ta nhân đơn thức đó với từng hạng tử của đa thức. Lời giải chi tiết :
Ta có: \(2{x^5}.\left( {3x - 2{x^2}} \right) = 6{x^6} - 4{x^7}\). Đáp án B
Câu 10 :
Hình chóp tam giác đều có cạnh đáy là 4 cm và chiều cao của mặt bên tương ứng với cạnh đáy là 3 cm có diện tích xung quanh là:
Đáp án : A Phương pháp giải :
Diện tích xung quanh của hình chóp tam giác đều bằng tổng diện tích các mặt bên của hình chóp. Lời giải chi tiết :
Diện tích một mặt bên của hình chóp là: \(\frac{1}{2}.3.4 = 6\left( {c{m^2}} \right)\) Diện tích xung quanh của hình chóp là: \(3.6 = 18\left( {c{m^2}} \right)\) Đáp án A
Câu 11 :
Phát biểu nào sau đây sai?
Đáp án : D Phương pháp giải :
Dựa vào dấu hiệu nhận biết hình chữ nhật. Lời giải chi tiết :
- Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật nên A đúng. - Tứ giác có ba góc vuông là hình chữ nhật nên B đúng. - Hình bình hành có một góc vuông là hình chữ nhật nên C đúng. Vậy đáp án D sai (vì hai đường chéo của hình chữ nhật không vuông góc với nhau). Đáp án D
Câu 12 :
Bộ ba số đo nào sau đây là độ dài ba cạnh của một tam giác vuông?
Đáp án : B Phương pháp giải :
Áp dụng định lí Pythagore đảo: nếu bình phương một cạnh bằng tổng bình phương hai cạnh còn lại trong tam giác thì tam giác là tam giác vuông. Lời giải chi tiết :
\({3^2} + {4^2} = 9 + 16 = 25 \ne 36 = {6^2}\) nên 3 cm, 4 cm, 6 cm không phải độ dài ba cạnh của một tam giác vuông. \({5^2} + {12^2} = 25 + 144 = 169 = {13^2}\) nên 5 cm, 12 cm, 13 cm là độ dài ba cạnh của một tam giác vuông. \({4^2} + {5^2} = 16 + 25 = 41 \ne 36 = {6^2}\) nên 4 cm, 5 cm, 6 cm không phải độ dài ba cạnh của một tam giác vuông. \({7^2} + {10^2} = 49 + 100 = 149 \ne 144 = {12^2}\) nên 7 cm, 10 cm, 12 cm không phải độ dài ba cạnh của một tam giác vuông. Đáp án B
II. Tự luận
Phương pháp giải :
1. Sử dụng hằng đẳng thức bình phương của một tổng và hiệu hai bình phương để phân tích đa thức thành nhân tử. 2. a) Sử dụng quy tắc trừ hai phân thức khác mẫu: Muốn trừ hai phân thức có mẫu thức khác nhau, ta quy đồng mẫu thức rồi đưa về quy tắc trừ hai phân thức có cùng mẫu thức. b) Sử dụng quy tắc nhân hai phân thức: Muốn nhân hai phân thức ta nhân các tử thức và nhân các mẫu thức với nhau: \(\frac{A}{B}.\frac{C}{D} = \frac{{AC}}{{BD}}\). Lời giải chi tiết :
1. Ta có: \(\begin{array}{l}{x^2} + 2xy + {y^2} - 4\\ = \left( {{x^2} + 2xy + {y^2}} \right) - 4\\ = {\left( {x + y} \right)^2} - {2^2}\\ = \left( {x + y - 2} \right)\left( {x + y + 2} \right)\end{array}\) 2. a) \(\frac{2}{{x + 1}} - \frac{{x - 3}}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\) \( = \frac{{2\left( {x - 1} \right)}}{{\left( {x + 1} \right)\left( {x - 1} \right)}} - \frac{{x - 3}}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\) \( = \frac{{2x - 2 - x + 3}}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\) \( = \frac{{x + 1}}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\) \( = \frac{1}{{x - 1}}\) b) \(\frac{{x - 2}}{{x + 3}}.\frac{{3x + 9}}{{{x^2} - 4}}\) \( = \frac{{\left( {x - 2} \right).\left( {3x + 9} \right)}}{{\left( {x + 3} \right).\left( {{x^2} - 4} \right)}}\) \( = \frac{{3.\left( {x - 2} \right).\left( {x + 3} \right)}}{{\left( {x + 3} \right).\left( {x - 2} \right).\left( {x + 2} \right)}}\) \( = \frac{3}{{x + 2}}\) Phương pháp giải :
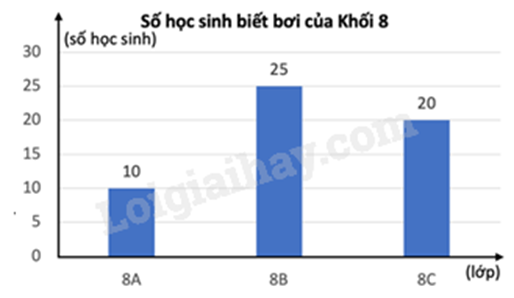
a) Dựa vào mục đích biểu diễn để lựa chọn biểu đồ phù hợp: Biểu đồ tranh: Tạo sự lôi cuốn, thu hút bằng hình ảnh. Biểu đồ cột: Sử dụng các chiều cao của các hình chữ nhật để biểu diễn số liệu. Thuận tiện trong việc so sánh. Biểu đồ đoạn thẳng: Biểu diễn sự thay đổi số liệu của đối tượng theo thời gian. Biểu đồ cột kép: So sánh một cách trực quan từng cặp số liệu của hai bộ dữ liệu cùng loại. Biểu đồ hình quạt tròn: Biểu thị tỉ lệ phần trăm từng loại số liệu so với toàn thể. b) Tính số học sinh biết bơi của cả ba lớp. Tỉ số phần trăm học sinh biết bơi của lớp 8A so với tổng số học sinh biết bơi = số học sinh biết bơi của lớp 8A : số học sinh biết bơi của cả ba lớp . 100%. Lời giải chi tiết :
a) Với bảng dữ liệu trên, ta nên chọn biểu đồ tranh hoặc biểu đồ cột. +) Ví dụ vẽ biểu đồ tranh:
+) Ví dụ vẽ biểu đồ cột:
b) Tổng số học sinh biết bơi Khối 8 là: \(10 + 25 + 20 = 55\) (học sinh) Số học sinh biết bơi của lớp 8A chiếm số phần trăm trên tổng số học sinh biết bơi của Khối 8 là: \(\frac{{10}}{{55}}.100\% \approx 18,2\% \) Vậy số học sinh biết bơi của lớp 8A chiếm khoảng 18,2% trên tổng số học sinh biết bơi của Khối 8. Phương pháp giải :
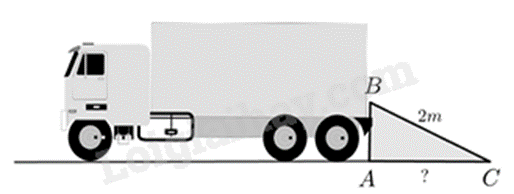
Ta cần tính độ dài đoạn AC. Áp dụng định lí Pythagore vào tam giác ABC vuông tại A để tính AC. Lời giải chi tiết :
Áp dụng định lí Pythagore vào tam giác ABC vuông tại A, ta có: \(A{C^2} = B{C^2} - A{B^2} = {2^2} - 1,{2^2} = 2,56 = 1,{6^2}\) Suy ra \(AC = 1,6\left( m \right)\) Vậy xe phải đậu cách cửa kho 1,6 mét để chân tấm ván vừa chạm đến cửa kho. Phương pháp giải :
Diện tích xung quanh của hình chóp tam giác đều bằng tổng diện tích các mặt bên của hình chóp. Lời giải chi tiết :
Đổi 60cm = 0,6m Diện tích một mặt bên của cột mốc là: \(\frac{1}{2}.1.0,6 = 0,3\left( {{m^2}} \right)\) Diện tích xung quanh của cột mốc là: \(3.0,3 = 0,9\left( {{m^2}} \right)\) Phương pháp giải :
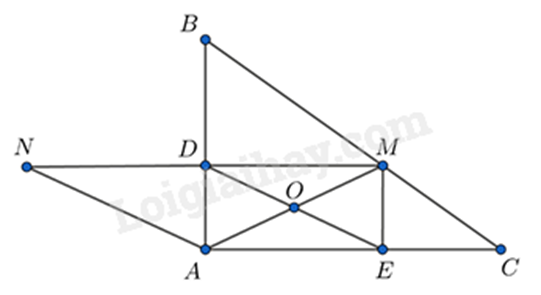
a) Chứng minh tứ giác ADME có 3 góc vuông nên là hình chữ nhật, suy ra AM = DE (hai đường chéo của hình chữ nhật bằng nhau. b) Chứng minh tứ giác ANDE có hai cạnh đối song song và bằng nhau nên là hình bình hành. Chứng minh AN = AM và AM = 2.AO nên AN = 2.AO. Lời giải chi tiết :
a) Xét tứ giác ADME có: \(\widehat {DAE} = 90^\circ \) (tam giác ABC vuông tại A) \(\widehat {ADM} = 90^\circ \) (MD vuông góc với AB tại D) \(\widehat {AEM} = 90^\circ \) (ME vuông góc với AC tại E) Suy ra tứ giác ADME là hình chữ nhật. Do đó AM = DE (hai đường chéo bằng nhau) b) Vì ADME là hình chữ nhật nên DM // AE và DM = AE. Xét tứ giác ANDE có: DN // AE (vì DM // AE) DN = AE (= DM) Suy ra tứ giác ANDE là hình bình hành. Suy ra AN = DE, mà AM = DE nên AN = AM. Mà AM = 2.AO (do O là giao điểm hai đường chéo của hình chữ nhật) Do đó AN = 2.AO.
|