Đề thi học kì 1 Toán 8 Chân trời sáng tạo - Đề số 6Tổng hợp đề thi học kì 2 lớp 8 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Khoa học tự nhiên Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:Đề bài
I. Trắc nghiệm
Chọn câu trả lời đúng trong mỗi câu sau:
Câu 1 :
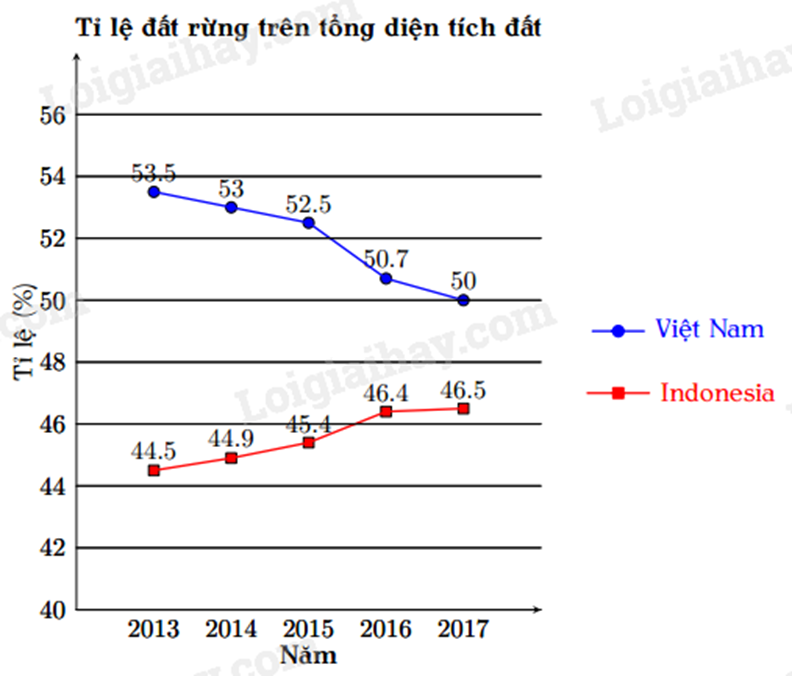
Cho biểu đồ tỉ lệ đất rừng trên tổng diện tích đất của hai quốc gia Việt Nam và Indonesia.
Dựa vào biểu đồ, ta thấy:
Câu 3 :
Trong các biểu thức sau, biểu thức nào không phải là đơn thức?
Câu 4 :
Biểu thức nào sau đây không phải là một phân thức đại số?
Câu 5 :
Dữ liệu nào sau đây là dữ liệu định lượng?
Câu 6 :
Chọn câu đúng:
Câu 8 :
Hằng đẳng thức nào sau đây là đúng?
Câu 9 :
Bậc của đơn thức −15xy4 là
Câu 10 :
Phân thức x−32x+5 được xác định khi:
Câu 11 :
Cặp đơn thức nào sau đây là hai đơn thức đồng dạng?
Câu 12 :
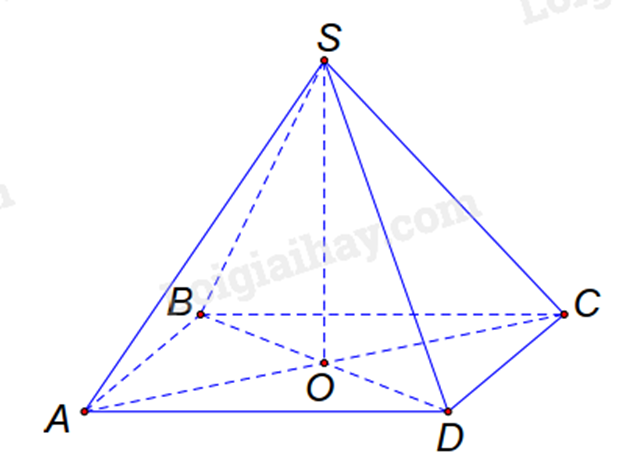
Mặt đáy của hình chóp tứ giác đều là
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Chọn câu trả lời đúng trong mỗi câu sau:
Câu 1 :
Cho biểu đồ tỉ lệ đất rừng trên tổng diện tích đất của hai quốc gia Việt Nam và Indonesia.
Dựa vào biểu đồ, ta thấy:
Đáp án : D Phương pháp giải :
Quan sát tỉ lệ đất rừng trên tổng diện tích của Việt Nam và Indonesia để xác định sự thay đổi. Lời giải chi tiết :
Qua các năm, tỉ lệ đất rừng trên tổng diện tích của Việt Nam và Indonesia đều thay đổi nên khẳng định A sai. Đường biểu diễn của Việt Nam luôn nằm trên Indonesia nên tỉ lệ đất rừng trên tổng diện tích đất của Việt Nam cao hơn của Indonesia nên khẳng định B sai, D đúng. Trong giai đoạn 2013 đến 2017, tỉ lệ đất rừng trên tổng diện tích của Việt Nam giảm dần, của Indonesia giảm dần nên C sai. Đáp án D
Đáp án : B Phương pháp giải :
Sử dụng các đặc điểm của hình chóp tứ giác đều. Lời giải chi tiết :
- Mặt đáy của hình chóp là ABCD nên A sai. - Các cạnh bên là: SA, SB, SC, SD nên B đúng. - Chiều cao của hình chóp tứ giác đều là đoạn SO nên C sai. - Các cạnh bên SA = SB = SC = SD nhưng không bằng SO (chiều cao) nên D sai. Đáp án B
Câu 3 :
Trong các biểu thức sau, biểu thức nào không phải là đơn thức?
Đáp án : C Phương pháp giải :
Đơn thức là biểu thức đại số chỉ gồm một số hoặc một biến, hoặc có dạng tích của những số và biến. Lời giải chi tiết :
Biểu thức 2x−y2 không phải là đơn thức. Đáp án C
Câu 4 :
Biểu thức nào sau đây không phải là một phân thức đại số?
Đáp án : D Phương pháp giải :
Một phân thức đại số (hay còn gọi là phân thức) là một biểu thức có dạng AB, trong đó A, B là những đa thức và B khác đa thức 0. Lời giải chi tiết :
7x2+y0x2 không phải là phân thức đại số vì có mẫu thức là đa thức 0x2=0. Đáp án D
Câu 5 :
Dữ liệu nào sau đây là dữ liệu định lượng?
Đáp án : C Phương pháp giải :
- Dữ liệu định lượng là những dữ liệu thống kê là số (số liệu) được biểu diễn bằng số thực. - Dữ liệu định tính là những dữ liệu thống kê không phải là số đươc biểu diễn bằng từ, chữ cái, kí hiệu,… Lời giải chi tiết :
Trong các dữ liệu trên, chỉ có dữ liệu “Số học sinh tham gia thi kéo co của lớp 8A” được biểu diễn bởi số nên là dữ liệu định lượng. Đáp án C
Câu 6 :
Chọn câu đúng:
Đáp án : B Phương pháp giải :
Dựa vào khái niệm của hình bình hành. Lời giải chi tiết :
Hình bình hành là tứ giác có hai cặp cạnh đối song song. Đáp án B
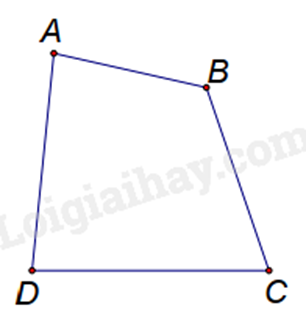
Đáp án : A Phương pháp giải :
Dựa vào các kiến thức liên quan đến tứ giác: đỉnh, cạnh kề, góc đối, đường chéo. Lời giải chi tiết :
Tứ giác ABCD có A, B, C, D là các đỉnh nên A đúng. Hai cạnh AB, CD là hai cạnh đối nhau nên B sai. Hai góc ˆA và ˆD là hai góc kề nhau nên C sai. AC và BD là hai đường chéo nên D sai. Đáp án A
Câu 8 :
Hằng đẳng thức nào sau đây là đúng?
Đáp án : B Phương pháp giải :
Áp dụng các hằng đẳng thức đáng nhớ đã học. Lời giải chi tiết :
Hằng đẳng thức đúng là (A−B)2=A2+B2−2AB. Đáp án B
Câu 9 :
Bậc của đơn thức −15xy4 là
Đáp án : C Phương pháp giải :
Bậc của đơn thức là tổng số mũ của các biến trong một đơn thức thu gọn với hệ số khác 0. Lời giải chi tiết :
Bậc của đơn thức −15xy4 là: 1 + 4 = 5. Đáp án C
Câu 10 :
Phân thức x−32x+5 được xác định khi:
Đáp án : A Phương pháp giải :
Phân thức xác định khi mẫu thức bằng 0. Lời giải chi tiết :
Phân thức x−32x+5 được xác định khi 2x+5≠0, suy ra 2x≠−5 nên x≠−52. Đáp án A
Câu 11 :
Cặp đơn thức nào sau đây là hai đơn thức đồng dạng?
Đáp án : D Phương pháp giải :
Hai đơn thức đồng dạng là hai đơn thức có hệ số khác 0 và có cùng phần biến. Lời giải chi tiết :
Hai đơn thức 9x3y2z và −12x3y2z có cùng phần biến x3y2z nên là hai đơn thức đồng dạng. Đáp án D
Câu 12 :
Mặt đáy của hình chóp tứ giác đều là
Đáp án : D Phương pháp giải :
Dựa vào đặc điểm của hình chóp tứ giác đều. Lời giải chi tiết :
Mặt đáy của hình chóp tứ giác đều là hình vuông. Đáp án D
II. Tự luận
Phương pháp giải :
a) Sử dụng quy tắc nhân đa thức với đa thức: ta nhân lần lượt các hạng tử của đa thức này với các hạng tử của đa thức kia. b) Sử dụng quy tắc cộng hai phân thức đại số cùng mẫu sau đó phân tích đa thức tử và mẫu để rút gọn phân thức. Lời giải chi tiết :
a) (x−3)(x2−x+5) =x3−3x2−x2+3x+5x−15=x3−(3x2+x2)+(3x+5x)−15=x3−4x2+8x−15 b) x23x+6+4x+43x+6 =x2+4x+43x+6=(x+2)23(x+2)=x+23 Phương pháp giải :
a) Kết hợp phương pháp nhóm hạng tử và hằng đẳng thức hiệu hai bình phương để phân tích đa thức thành nhân tử. b) Sử dụng hằng đẳng thức lập phương của một hiệu để rút gọn A, sau đó thay x=−28 vào A để tính giá trị của biểu thức. Lời giải chi tiết :
a) Ta có: x2−y2+2x+1=(x+2x+1)−y2=(x+1)2−y2=(x+1−y)(x+1+y) b) Ta có: A=−x3+6x2−12x+8=8−12x+6x2−x3=(2−x)3 Thay x=−28 vào biểu thức A, ta được: A=[2−(−28)]3=(2+28)3=303=27000 Phương pháp giải :
a) Dựa vào mục đích biểu diễn của các loại biểu đồ để lựa chọn biểu đồ thích hợp. Biểu đồ tranh: Tạo sự lôi cuốn, thu hút bằng hình ảnh. Biểu đồ cột: Sử dụng các chiều cao của các hình chữ nhật để biểu diễn số liệu. Thuận tiện trong việc so sánh. Biểu đồ đoạn thẳng: Biểu diễn sự thay đổi số liệu của đối tượng theo thời gian. Biểu đồ cột kép: So sánh một cách trực quan từng cặp số liệu của hai bộ dữ liệu cùng loại. Biểu đồ hình quạt tròn: Biểu thị tỉ lệ phần trăm từng loại số liệu so với toàn thể. b) - So sánh tỉ lệ xếp loại. - Kiểm tra xem đa số thành viên nhận bình xét ở mức nào để kiểm tra khẳng định. Lời giải chi tiết :
a) Vì sau khi bình xét, tỉ lệ xếp loại thi đua theo bốn mức: Tốt, Khá, Trung bình, Chưa đạt lần lượt là 30%; 40%; 20%; 10% nên ta chọn biểu đồ quạt biểu diễn bình xét thi đua cho mỗi thành viên trong một tổ sản xuất: b) - Quan sát biểu đồ, ta thấy tỉ lệ xếp loại thi đua ở mức Khá là cao nhất. - Tổ trưởng nhận xét đa số các thành viên nhận bình xét ở mức Tốt là không đúng vì 40% thành viên nhận mức bình xét ở mức Khá, còn mức Tốt chỉ có 30% ( 40% > 30% ). Phương pháp giải :
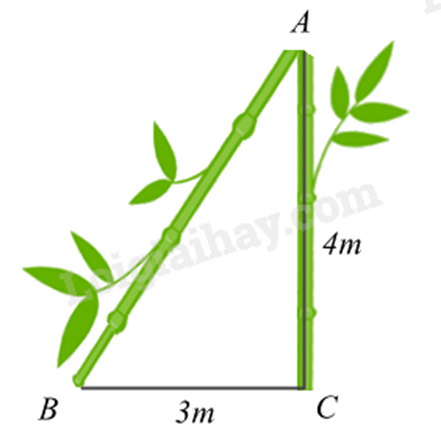
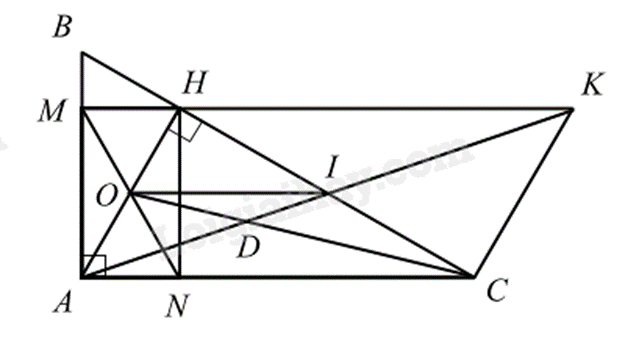
1. Áp dụng định lí Pythagore trong tam giác vuông để tính AB. Chiều cao của cây lúc đầu bằng tổng đoạn AB và AC. 2. a) Chứng minh AMHN có 3 góc vuông nên là hình chữ nhật. b) - Chứng minh tứ giác AHKC là hình bình hành suy ra AC // HK và AH = CK. - Chỉ ra AH = MN (do AMHN là hình chữ nhật) suy ra CK = MN. c) Chỉ ra D là trọng tâm của tam giác AHC, suy ra AD = 23 AI. Chỉ ra AI=12AK nên AK = 3AD. Lời giải chi tiết :
1.
Xét tam giác ABC vuông tại C. Áp dụng định lí Pythagore, ta có: AB2=AC2+BC2=42+32=25 suy ra AB=5(m) (vì AB>0) Chiều cao của cây lúc đầu là: AC + AB = 4 + 5 = 9 (m). 2.
a) Vì tam giác ABC vuông tại A nên ˆA=90∘. Vì HM⊥AB(M∈AB) HN⊥AC(N∈AC) nên ^HMA=^HNA=90∘. Tứ giác AMHN có: ˆA=^HMA=^HNA=90∘ nên là hình chữ nhật. b) Xét tứ giác AHKC có: HC cắt AK tại I và AI = IK (gt), HI = IC (gt) suy ra tứ giác AHKC là hình bình hành, do đó AC//HK và AH = CK. Mà AH = MN (hai đường chéo của hình chữ nhật AMHN bằng nhau) nên MN = CK. c) Xét tam giác AHC có CO và AI là hai đường trung tuyến và CO cắt AI tại D nên D là trọng tâm của tam giác AHC. Do đó AD=23AI (tính chất của trọng tâm) Mà AI=12AK (do I là trung điểm của AK) Do đó AD=23.12AK=13AK hay AK=3AD. Phương pháp giải :
Sử dụng các hằng đẳng thức đáng nhớ để biến đổi đưa biểu thức về dạng A−B(x)−C(x) với B(x),C(x) là hai biểu thức bậc hai. Khi đó A−B(x)−C(x)≤A, khi đó giá trị giá trị lớn nhất của biểu thức là A khi B(x)=0 và C(x)=0. Lời giải chi tiết :
Ta có: B=2014−2x2−y2+2xy−8x+2y=2024−1−9−x2−x2−y2+2xy−8x+2y=2024−(x2−2xy+y2)−1−x2−8x+2y−9=2024−[(x−y)2−2x+2y−1]−x2−6x−9=2024−[(x−y)2+2(x−y)+1]−(x2+6x+9)=2024−(x−y+1)2−(x+3)2 Vì (x−y+1)2≥0 với mọi x, y và (x+3)2≥0 với mọi x nên B=2024−(x−y+1)2−(x+3)2≤0 với mọi x, y. Dấu “=” xảy ra khi x+3=0 và x−y+1=0, suy ra x=−3 và y=−2. Vậy giá trị lớn nhất của B = 2024 khi x=−3 và y=−2.
|