Đề thi học kì 1 Toán 8 - Đề số 4 - Chân trời sáng tạoTổng hợp đề thi học kì 2 lớp 8 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Khoa học tự nhiên Phần trắc nghiệm (3 điểm) Câu 1: Kết quả thương của phép chia (left( 3x{{y}^{2}}-2{{x}^{2}}y+{{x}^{3}} right):left( -frac{1}{2}x right)) là :Đề bài
I. Trắc nghiệm
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1 :
Kết quả thương của phép chia \(\left( {3x{y^2} - 2{x^2}y + {x^3}} \right):\left( { - \frac{1}{2}x} \right)\) là:
Câu 2 :
Giá trị của đa thức \({x^3}y - 14{y^3} - 6x{y^2} + y + 2\) tại x = -1 ; y = 0,5 là:
Câu 3 :
Phân thức \(\frac{2}{{x - 3}}\) không có nghĩa khi:
Câu 4 :
Phân thức nghịch đảo của phân thức \(\frac{2}{{x - 4}}\left( {x \ne 4} \right)\) là:
Câu 5 :
Rút gọn phân thức \(\frac{{x - 3}}{{{x^2} - 9}}\left( {x \ne \pm 3} \right)\), ta được kết quả:
Câu 6 :
Hai đường chéo của hình chữ nhật
Câu 7 :
Một tứ giác là hình bình hành nếu nó là:
Câu 8 :
Những tứ giác nào sau đây có hai đường chéo bằng nhau?
Câu 9 :
Độ dài một cạnh góc vuông và cạnh huyền của một tam giác vuông lần lượt là 3cm và 5cm. Diện tích của tam giác vuông đó là:
Câu 10 :
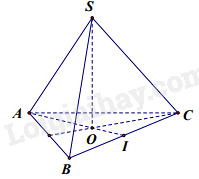
Cho hình khối chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên bằng 2a. Tính thể tích V của khối chóp S.ABC.
Câu 11 :
Một hình chóp tứ giác đều S.ABCD có độ dài trung đoạn là 12cm và đáy là hình vuông có chu vi là 40cm. Diện tích xung quanh của hình chóp tứ giác đều đó là:
Câu 12 :
Bạn Châu vẽ biểu đồ hình quạt tròn như hình bên để biểu diễn tỉ lệ các loại sách trong thư viện: Khoa học (KH), Kĩ thuật và công nghệ (KT & CN), Văn học và Nghệ thuật (VH – NT); Sách khác. Những dữ liệu mà bạn Châu nêu ra trong biểu đồ hình quạt tròn dữ liệu nào chưa hợp lí?
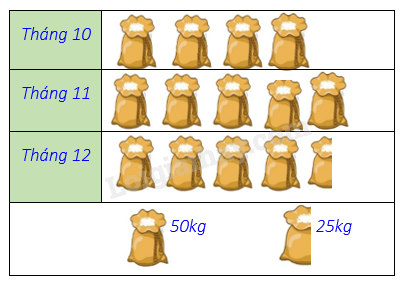
Biểu đồ tranh ở hình bên thống kê số gạo bán của một cửa hàng trong ba tháng cuối năm 2020.
Câu 13
Nêu số kg gạo bán được ở tháng 12?
Câu 14
Lựa chọn biểu đồ nào để biểu diễn các dữ liệu thống kê có trong biểu đồ tranh ở hình bên?
Câu 15
So tháng 10 số gạo bán được của tháng 11 tăng bao nhiêu phần trăm?
II. Tự luận
Câu 3 :
Biểu đồ hình quạt tròn biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) các thị trường cung cấp cà phê cho Tây Ban Nha trong 7 tháng đầu năm 2022.
(Nguồn: Eurostat) a) Trong 7 tháng đầu năm 2022 thị trường nào cung cấp cà phê cho Tây Ban Nha là nhiều nhất, ít nhất? b) Biết lượng cà phê mà tất cả các thị trường cung cấp cho Tây Ban Nha trong 7 tháng đầu năm 2022 là 222 956 tấn. Lập bảng thống kê lượng cà phê mà các thị trường cung cấp cà phê cho Tây Ban Nha trong 7 tháng đầu năm 2022 theo mẫu sau:
Lời giải và đáp án
I. Trắc nghiệm
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1 :
Kết quả thương của phép chia \(\left( {3x{y^2} - 2{x^2}y + {x^3}} \right):\left( { - \frac{1}{2}x} \right)\) là:
Đáp án : C Phương pháp giải :
Sử dụng quy tắc chia đa thức cho đơn thức. Lời giải chi tiết :
Ta có: \(\begin{array}{l}\left( {3x{y^2} - 2{x^2}y + {x^3}} \right):\left( { - \frac{1}{2}x} \right)\\ = 3x{y^2}:\left( { - \frac{1}{2}x} \right) - 2{x^2}y:\left( { - \frac{1}{2}x} \right) + {x^3}:\left( { - \frac{1}{2}x} \right)\\ = - 6{y^2} + 4xy - 2{x^2}\end{array}\)
Câu 2 :
Giá trị của đa thức \({x^3}y - 14{y^3} - 6x{y^2} + y + 2\) tại x = -1 ; y = 0,5 là:
Đáp án : D Phương pháp giải :
Thay x = -1 ; y = 0,5 vào biểu thức để tính giá trị. Lời giải chi tiết :
Thay x = -1 ; y = 0,5 vào biểu thức, ta được: \(\begin{array}{l}{( - 1)^3}.0,5 - 14{(0,5)^3} - 6( - 1){(0,5)^2} + 0,5 + 2\\ = - 0,5 - 14.0,125 + 6.0,25 + 0,5 + 2\\ = - 0,5 - 1,75 + 1,5 + 0,5 + 2\\ = 1,75\end{array}\)
Câu 3 :
Phân thức \(\frac{2}{{x - 3}}\) không có nghĩa khi:
Đáp án : A Phương pháp giải :
Phân thức không có nghĩa khi mẫu thức bằng 0. Lời giải chi tiết :
Phân thức \(\frac{2}{{x - 3}}\) không có nghĩa khi x – 3 = 0 hay x = 3.
Câu 4 :
Phân thức nghịch đảo của phân thức \(\frac{2}{{x - 4}}\left( {x \ne 4} \right)\) là:
Đáp án : A Phương pháp giải :
Hai phân thức được gọi là nghịch đảo nếu tích của chúng bằng 1. Lời giải chi tiết :
Phân thức nghịch đảo của phân thức \(\frac{2}{{x - 4}}\) là: \(1:\frac{2}{{x - 4}} = \frac{{x - 4}}{2}\).
Câu 5 :
Rút gọn phân thức \(\frac{{x - 3}}{{{x^2} - 9}}\left( {x \ne \pm 3} \right)\), ta được kết quả:
Đáp án : B Phương pháp giải :
Sử dụng các quy tắc tính với phân thức để rút gọn. Lời giải chi tiết :
Ta có: \(\frac{{x - 3}}{{{x^2} - 9}} = \frac{{x - 3}}{{\left( {x - 3} \right)\left( {x + 3} \right)}} = \frac{1}{{x + 3}}\).
Câu 6 :
Hai đường chéo của hình chữ nhật
Đáp án : C Phương pháp giải :
Sử dụng tính chất của hình chữ nhật. Lời giải chi tiết :
Hai đường chéo của hình chữ nhật bằng nhau nên chọn đáp án C.
Câu 7 :
Một tứ giác là hình bình hành nếu nó là:
Đáp án : C Phương pháp giải :
Dựa vào kiến thức về hình bình hành. Lời giải chi tiết :
Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành nên chọn đáp án C.
Câu 8 :
Những tứ giác nào sau đây có hai đường chéo bằng nhau?
Đáp án : B Phương pháp giải :
Dựa vào kiến thức về các hình đã học. Lời giải chi tiết :
Những tứ giác có hai đường chéo bằng nhau là: hình thang cân, hình chữ nhật, hình vuông nên chọn đáp án B.
Câu 9 :
Độ dài một cạnh góc vuông và cạnh huyền của một tam giác vuông lần lượt là 3cm và 5cm. Diện tích của tam giác vuông đó là:
Đáp án : C Phương pháp giải :
Sử dụng định lí Pythagore để tính. Lời giải chi tiết :
Tam giác ABC vuông tại A có AC = 3cm, BC = 5cm. Áp dụng định lí Pythagore vào tam giác ABC, ta có: \(A{B^2} + A{C^2} = B{C^2}\) \(\begin{array}{l} \Rightarrow A{B^2} = B{C^2} - A{C^2} = {5^2} - {3^2} = 16\\ \Rightarrow AB = \sqrt {16} = 4(cm)\end{array}\) Diện tích của tam giác vuông đó là: \({S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}4.3 = 6\left( {c{m^2}} \right)\).
Câu 10 :
Cho hình khối chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên bằng 2a. Tính thể tích V của khối chóp S.ABC.
Đáp án : B Phương pháp giải :
Sử dụng tính chất đường trung bình. Lời giải chi tiết :
Gọi I là trung điểm của cạnh BC, vì tam giác ABC là tam giác đều nên AI là đường trung tuyến đồng thời là đường cao của tam giác ABC. Áp dụng định lí Pythagore vào tam giác ABI, ta có: \(\begin{array}{l}A{I^2} = A{B^2} - B{I^2} = {a^2} - {\left( {\frac{a}{2}} \right)^2} = \frac{{3{a^2}}}{4}\\ \Rightarrow AI = \sqrt {\frac{{3{a^2}}}{4}} = \frac{{a\sqrt 3 }}{2}\end{array}\)\(\) \(AO = \frac{2}{3}AI = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\) (O là trọng tâm) Áp dụng định lí Pythagore vào tam giác SOA, ta có: \(\begin{array}{l}S{O^2} = S{A^2} - A{O^2} = {\left( {2a} \right)^2} - {\left( {\frac{{a\sqrt 3 }}{3}} \right)^2} = \frac{{11{a^2}}}{3}\\ \Rightarrow SO = \sqrt {\frac{{11{a^2}}}{3}} = \frac{{a\sqrt {33} }}{3}\end{array}\) Vậy thể tích khối chóp S.ABC là: \(\begin{array}{l}V = \frac{1}{3}.SO.{S_{ABC}} = \frac{1}{3}.\frac{{a\sqrt {33} }}{3}\left( {\frac{1}{2}\frac{{a\sqrt 3 }}{2}.a} \right)\\ = \frac{{{a^3}\sqrt {11} }}{{12}}\end{array}\)
Câu 11 :
Một hình chóp tứ giác đều S.ABCD có độ dài trung đoạn là 12cm và đáy là hình vuông có chu vi là 40cm. Diện tích xung quanh của hình chóp tứ giác đều đó là:
Đáp án : D Phương pháp giải :
Sử dụng công thức tính diện tích xung quanh của hình chóp tứ giác đều. Lời giải chi tiết :
Diện tích xung quanh của hình chóp tứ giác đều đó là: \({S_{xq}} = \frac{{40}}{2}.12 = 240\left( {c{m^2}} \right)\)
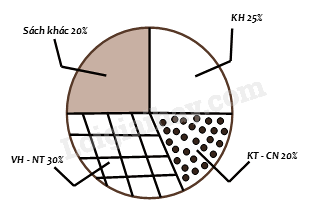
Câu 12 :
Bạn Châu vẽ biểu đồ hình quạt tròn như hình bên để biểu diễn tỉ lệ các loại sách trong thư viện: Khoa học (KH), Kĩ thuật và công nghệ (KT & CN), Văn học và Nghệ thuật (VH – NT); Sách khác. Những dữ liệu mà bạn Châu nêu ra trong biểu đồ hình quạt tròn dữ liệu nào chưa hợp lí?
Đáp án : A Phương pháp giải :
Quan sát biểu đồ để chỉ ra dữ liệu chưa hợp lí. Lời giải chi tiết :
Trong biểu đồ trên, ta thấy tỉ lệ của sách khác (20%) bằng tỉ lệ sách KT – CN (20%) nhưng phần biểu diễn của sách khác lại bằng với phần biểu diễn của sách KN (25%). nên dữ liệu sách khác, sách KT – CN hoặc sách KH chưa hợp lý. Vì tổng tỉ lệ các loại sách là 100%, mà tổng số phần trăm trong biểu đồ trên là 30% + 20% + 25% + 20% = 95% < 100%. Vậy ta suy ra dữ liệu chưa hợp lí là dữ liệu sách khác. Tỉ lệ của sách khác phải là 25% bằng với tỉ lệ của sách KH. Biểu đồ tranh ở hình bên thống kê số gạo bán của một cửa hàng trong ba tháng cuối năm 2020.
Câu 13
Nêu số kg gạo bán được ở tháng 12?
Đáp án : C Phương pháp giải :
Quan sát biểu đồ tranh để trả lời câu hỏi. Lời giải chi tiết :
Số kg gạo bán được ở tháng 12 là: 50.4 + 25 = 225 (kg). Câu 14
Lựa chọn biểu đồ nào để biểu diễn các dữ liệu thống kê có trong biểu đồ tranh ở hình bên?
Đáp án : C Phương pháp giải :
Quan sát biểu đồ tranh để trả lời câu hỏi. Lời giải chi tiết :
Với dự liệu trong biểu đồ tranh trên, ta có thể biểu diễn các dữ liệu thống kê bằng biểu đồ cột. Câu 15
So tháng 10 số gạo bán được của tháng 11 tăng bao nhiêu phần trăm?
Đáp án : A Phương pháp giải :
Quan sát biểu đồ tranh để trả lời câu hỏi. Lời giải chi tiết :
Số gạo tháng 10 bán được là: 50.4 = 200 (kg). Số gạo tháng 11 bán được là: 50.5 = 250 (kg). So với tháng 10, số gạo bán được của tháng 11 tăng là: 250 – 200 = 50 (kg). Số gạo bán được của tháng 11 tăng so với tháng 10 số phần trăm là: \(\frac{{50}}{{200}}.100 = 25(\% )\)
II. Tự luận
Phương pháp giải :
Sử dụng các phép tính với đa thức để rút gọn biểu thức. Lời giải chi tiết :
a) \(A = 2xy + \frac{1}{2}x.\left( {2x - 4y + 4} \right) - x\left( {x + 2} \right)\) \(\begin{array}{l} = 2xy + {x^2} - 2xy + 2x - {x^2} - 2x\\ = 0\end{array}\) Vì A = 0 nên biểu thức A không phụ thuộc vào giá trị của biến. b) \(B = {\left( {x + 2} \right)^2} - {\left( {x - 3} \right)^2} - 10x\) \(\begin{array}{l} = {\left( {x + 2} \right)^2} - {\left( {x - 3} \right)^2} - 10x\\ = \left( {x + 2 - x + 3} \right)\left( {x + 2 + x - 3} \right) - 10x\\ = 5\left( {2x - 1} \right) - 10x\\ = 10x - 5 - 10x\\ = - 5\end{array}\) Vì B = -5 nên biểu thức B không phụ thuộc vào giá trị của biến. Phương pháp giải :
a) Xác định điều kiện xác định của M. Sử dụng các quy tắc tính của phân thức để rút gọn M. b) Để phân thức M nguyên thì tử thức chia hết cho mẫu thức. Lời giải chi tiết :
a) Ta có: \(M = \frac{{2\left( {1 - 9{x^2}} \right)}}{{3{x^2} + 6x}}:\frac{{2 - 6x}}{{3x}}\left( {x \ne 0;x \ne - 2} \right)\) \(\begin{array}{l} = \frac{{2\left( {1 - 3x} \right)\left( {1 + 3x} \right)}}{{3x\left( {x + 2} \right)}}:\frac{{2(1 - 3x)}}{{3x}}\\ = \frac{{2\left( {1 - 3x} \right)\left( {1 + 3x} \right)}}{{3x\left( {x + 2} \right)}}.\frac{{3x}}{{2\left( {1 - 3x} \right)}}\\ = \frac{{1 + 3x}}{{x + 2}}\end{array}\) Vậy \(M = \frac{{1 + 3x}}{{x + 2}}\). b) Ta có: \(M = \frac{{1 + 3x}}{{x + 2}} = \frac{{3x + 6 - 5}}{{x + 2}} = 3 - \frac{5}{{x + 2}}\) Để M nguyên thì \(\frac{5}{{x + 2}}\) nguyên, hay \(\left( {x + 2} \right) \in U\left( 5 \right) = \left\{ { \pm 1; \pm 5} \right\}\). Ta có bảng giá trị sau:
Vậy \(x \in \left\{ { - 3; - 2; - 7;3} \right\}\) thì M có giá trị nguyên.
Câu 3 :
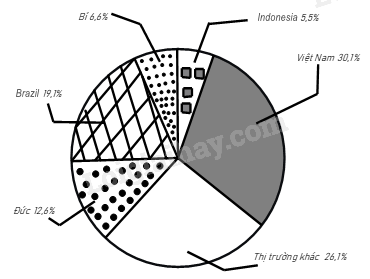
Biểu đồ hình quạt tròn biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) các thị trường cung cấp cà phê cho Tây Ban Nha trong 7 tháng đầu năm 2022.
(Nguồn: Eurostat) a) Trong 7 tháng đầu năm 2022 thị trường nào cung cấp cà phê cho Tây Ban Nha là nhiều nhất, ít nhất? b) Biết lượng cà phê mà tất cả các thị trường cung cấp cho Tây Ban Nha trong 7 tháng đầu năm 2022 là 222 956 tấn. Lập bảng thống kê lượng cà phê mà các thị trường cung cấp cà phê cho Tây Ban Nha trong 7 tháng đầu năm 2022 theo mẫu sau:
Phương pháp giải :
Dựa vào biểu đồ để trả lời câu hỏi. Lời giải chi tiết :
a) Trong 7 tháng đầu năm 2022, thị trường cung cấp cà phê cho Tây Ban Nha nhiều nhất là Việt Nam với 30,1%; thị trường cung cấp ít nhất là Indonesia với 5,5%. b) Lượng cà phê Đức cung cấp cho Tây Ban Nha là: 222 956.12,6% = 28 092,456 (tấn) Lượng cà phê Brazil cung cấp cho Tây Ban Nha là: 222 956.19,1% = 42 584,596 (tấn) Lượng cà phê Bỉ cung cấp cho Tây Ban Nha là: 222 956.6,6% = 14 715,096 (tấn) Lượng cà phê Indonesia cung cấp cho Tây Ban Nha là: 222 956.5,5% = 12 262,58 (tấn) Lượng cà phê Việt Nam cung cấp cho Tây Ban Nha là: 222 956.30,1% = 67 109,756 (tấn) Lượng cà phê thị trường khác cung cấp cho Tây Ban Nha là: 222 956.26,1% = 58 191,516 (tấn) Ta có bảng giá trị:
Phương pháp giải :
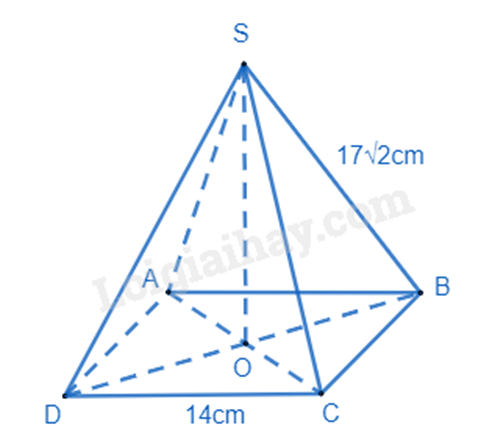
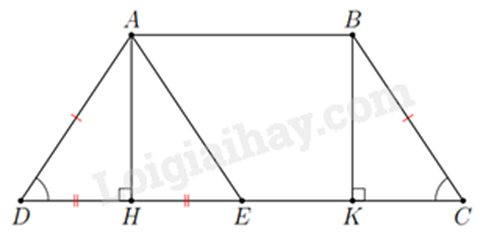
1. Dựa vào định lí Pythagore và công thức tính thể tích giá đèn cầy để tính. 2. a) Tứ giác \(ABKH\) là hình chữ nhật. b) \(\Delta ADH = \Delta BKC\) (ch - gn). Nên suy ra \(DH = KC\). c) Dễ thấy \(HE + EK = EK + KC\) \( \Rightarrow \) \(AB = EC\). Do đó, \(ABCE\) là hình bình hành. Lời giải chi tiết :
1.
Hình chóp tứ giác đều S.ABCD có đáy là hình vuông, SO là đường cao của hình chóp S.ABCD. Xét tam giác ABC vuông tại B, áp dụng định lí Pythagore, ta có: \(A{C^2} = A{B^2} + B{C^2} = {14^2} + {14^2} = 128\) suy ra \(AC = \sqrt {128} = 14\sqrt 2 (cm)\) Do đó \(AO = \frac{{14\sqrt 2 }}{2} = 7\sqrt 2 (cm)\) Xét tam giác SAO vuông tại O, áp dụng định lí Pythagore, ta có: \(S{O^2} = S{A^2} - A{O^2} = {\left( {17\sqrt 2 } \right)^2} - {\left( {7\sqrt 2 } \right)^2} = 480\) suy ra \(SO = 4\sqrt {30}(cm)\) Thể tích giá đèn cầy S.ABCD là: \(V = \frac{1}{3}{.4\sqrt {30}.14^2} \approx 1431\left( {c{m^3}} \right)\) Vậy thể tích giá đèn cầy là 1431cm3. 2.
a) Ta có: AB // CD (ABCD là hình thang cân), AH \( \bot \) CD => AH \( \bot \) AB => \(\widehat {BAH} = {90^0}\). Xét tứ giác ABKH có: \(\widehat {BAH} = {90^0};\widehat H = {90^0};\widehat K = {90^0}\) suy ra ABKH là hình chữ nhật. b) ABKH là hình chữ nhật => AH = BK. ABCD là hình thang cân nên AD = BC. Xét tam giác AHD và BKC có: \(\left\{ \begin{array}{l}AD = BC\\AH = BK(cmt)\\\widehat H = \widehat K = {90^0}\end{array} \right. \Rightarrow \Delta AHD = \Delta BKC(ch - cgv)\) => DH = CK. (đpcm) c) Ta có: AB = HK (ABKH là hình chữ nhật) Ta có E đối xứng với D qua H => DH = HE => HK = HE + EK = DH + EK = KC + EK = EC. => AB = EC. Mà AB // CE, do đó ABCE là hình bình hành. Phương pháp giải :
Biến đổi biểu thức bằng cách sử dụng hằng đẳng thức. Lời giải chi tiết :
Ta có: \(4{x^2} - 12x + 15 = \left( {4{x^2} - 2.2x.3 + 9} \right) + 6 = {\left( {2x - 3} \right)^2} + 6\). Vì \({\left( {2x - 3} \right)^2} \ge 0,\forall x \in \mathbb{R}\) nên \({\left( {2x - 3} \right)^2} + 6 \ge 6,\forall x \in \mathbb{R}\). Dấu “=” xảy ra là giá trị nhỏ nhất của biểu thức A. \(\min A = 6 \Leftrightarrow 2x - 3 = 0 \Leftrightarrow x = \frac{3}{2}\). Vậy giá trị nhỏ nhất của biểu thức A là 6 khi \(x = \frac{3}{2}\).
|