Đề thi giữa kì 1 Toán 8 - Đề số 1

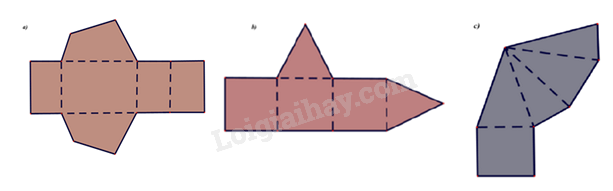
Đề bài

Phần trắc nghiệm (3 điểm)

Câu 1: Tìm hệ số trong đơn thức \( - 36{a^2}{b^2}{x^2}{y^3}\) với a,b là hằng số.

A. \( - 36\)

B. \( - 36{a^2}{b^2}\)

C. \(36{a^2}{b^2}\)

D. \( - 36{a^2}\)

Câu 2: Giá trị của đa thức \(4{x^2}y - \frac{2}{3}x{y^2} + 5xy - x\) tại \(x = 2;y = \frac{1}{3}\) là

A. \(\frac{{176}}{{27}}\)

B. \(\frac{{27}}{{176}}\)

C. \(\frac{{17}}{{27}}\)

D. \(\frac{{116}}{{27}}\)

Câu 3: Chọn câu sai.

A. \({\left( {x + y} \right)^2} = \left( {x + y} \right)\left( {x + y} \right)\).

B. \({x^2} - {y^2} = \left( {x + y} \right)\left( {x - y} \right)\).

C. \({\left( { - x - y} \right)^2} = {\left( { - x} \right)^2} - 2\left( { - x} \right)y + {y^2}\).

D. \(\left( {x + y} \right)\left( {x + y} \right) = {y^2} - {x^2}\).

Câu 4: Có bao nhiêu giá trị \(x\) thỏa mãn \({\left( {2x - 1} \right)^2} - {\left( {5x - 5} \right)^2} = 0\)

A. \(0\)

B. \(1\)

C. \(2\)

D. \(3\)

Câu 5: Chọn câu đúng.

A. \(8 + 12y + 6{y^2} + {y^3} = \left( {8 + {y^3}} \right)\).

B. \({a^3} + 3{a^2} + 3a + 1 = {\left( {a + 1} \right)^3}\).

C. \({\left( {2x - y} \right)^3} = 2{x^3} - 6{x^2}y + 6xy - {y^3}\).

D. \({\left( {3a + 1} \right)^3} = 3{a^3} + 9{a^2} + 3a + 1\).

Câu 6: Tứ giác ABCD có \(AB = BC,CD = DA,\;\hat B = {90^0};\;\hat D = {120^0}\). Hãy chọn câu đúng nhất:

A. \(\hat A = {85^0}\).

B. \(\hat C = {75^0}\).

C. \(\hat A = {75^0}\).

D. Chỉ \(B\) và \(C\) đúng.

Câu 7: Hình thang ABCD (AB//CD) có số đo góc D bằng \({70^0},\)  số đo góc \(A\) là:

A. \({130^0}\)

B. \({90^0}\)

C. \({110^0}\)

D. \({120^0}\)

Câu 8: Cho hình chóp tam giác đều có độ dài cạnh đáy là 5cm, độ dài trung đoạn của hình chóp là 6cm. Diện tích xung quanh của hình chóp tam giác đều đó là :

A. \(40c{m^2}\)

B. \(36c{m^2}\)

C. \(45c{m^2}\)

D. \(50c{m^2}\)

Câu 9: Hình chóp tứ giác đều có mặt bên là hình gì?

A. Tam giác cân.

B. Tam giác vuông.

C. Tam giác vuông cân.

D. Đáp án khác.

Câu 10: Trong các hình vẽ bên dưới hình nào có thể gấp theo nét đứt để được hình chóp tứ giác đều:

A. Hình b và c.

B. Hình c.

C. Hình a và c.

D. Hình b.

Câu 11: Cho \(\Delta\)ABC vuông tại A có AB = 4 cm, BC = 5 cm . Diện tích ABC bằng

A. 6cm².

B. 10cm².

C. 12cm².

D. 20cm².

Câu 12: Cho hình chóp S.ABCD đều có thể tích bằng 200cm³ , chiều cao SO bằng 12cm. Độ dài cạnh bên của hình chóp tứ giác đó là :

A. 12cm.

B. 13cm.

C. 11cm.

D. 16cm.

Phần tự luận (7 điểm)

Bài 1. (2 điểm) Cho biểu thức: \(A = 3x(2x - y) + (x - y)(x + y) - 7{x^2} + {y^2}\).

a) Thu gọn A.

b) Tính giá trị của A biết x = \(\frac{{ - 2}}{3}\) và y = 2

Bài 2. (1,5 điểm) Tìm x biết:

a) \({\left( {x - 3} \right)^2} - {x^2} = 0\)

b) \({x^3} - 5{x^2} - 9x + 45 = 0\)

c) \(\left( {5x - 3} \right)\left( {2x + 1} \right) - {\left( {2x - 1} \right)^2} + 4 = 0\)

Bài 3. (1 điểm) Người ta thiết kế chậu trồng cây có dạng hình chóp tam giác đều (như hình vẽ bên) biết: cạnh đáy khoảng 20cm, chiều cao khoảng 35 cm, độ dài trung đoạn khoảng 21 cm.

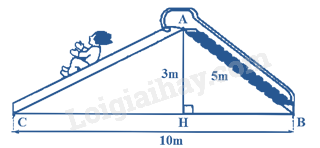
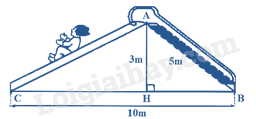
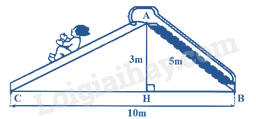
a/ Người ta muốn sơn các bề mặt xung quanh chậu . Hỏi diện tích bề mặt cần sơn là bao nhiêu?

b/ Tính thể tích của chậu trồng cây đó (làm tròn kết quả đến hàng phần trăm). Biết đường cao của mặt đáy hình chóp là 17cm.

Bài 4. (2 điểm)

1. Cho tứ giác \(ABCD\) có \(AB = BC\); \(CD = DA\). Biết \(\hat B = {100^0}\), \(\hat D = {80^0}\). Tính \(\hat A\) và \(\hat C\).

2. Tính chiều dài đường trượt AC trong hình vẽ trên (kết quả làm tròn hàng phần mười).

Bài 5. (0,5 điểm) Cho a + b + c. Chứng minh \({a^3} + {b^3} + {c^3} = 3abc\).

- Hết -

Lời giải

Phần trắc nghiệm 

Câu 1: Tìm hệ số trong đơn thức \( - 36{a^2}{b^2}{x^2}{y^3}\) với a,b là hằng số.

Phương pháp

Sử dụng lý thuyết về đơn thức thu gọn:

Đơn thức thu gọn là đơn thức chỉ gồm tích của một số với các biến mà mỗi biến đã được nâng lên lũy thừa với số mũ nguyên dương. Số nói trên gọi là hệ số, phần còn lại gọi là phần biến của đơn thức thu gọn.

Lời giải

Đơn thức \( - 36{a^2}{b^2}{x^2}{y^3}\) với a,b là hằng số có hệ số là \( - 36{a^2}{b^2}.\)

Đáp án B.

Câu 2: Giá trị của đa thức \(4{x^2}y - \frac{2}{3}x{y^2} + 5xy - x\) tại \(x = 2;y = \frac{1}{3}\) là

Phương pháp

Thay \(x = 2;y = \frac{1}{3}\) vào đa thức rồi tính toán.

Lời giải

Thay \(x = 2;y = \frac{1}{3}\) vào đa thức \(4{x^2}y - \frac{2}{3}x{y^2} + 5xy - x\) ta được \({4.2^2}.\frac{1}{3} - \frac{2}{3}.2.{\left( {\frac{1}{3}} \right)^2} + 5.2.\frac{1}{3} - 2\)\( = \frac{{176}}{{27}}\).

Đáp án A.

Câu 3: Chọn câu sai.

Phương pháp

Sử dụng các công thức \({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\), \({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\) , \({A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right)\)

Lời giải

Ta có \(\left( {x + y} \right)\left( {x + y} \right) = {\left( {x + y} \right)^2} = {x^2} + 2xy + {y^2} \ne {y^2} - {x^2}\) nên câu D sai.

Đáp án D.

Câu 4: Có bao nhiêu giá trị \(x\) thỏa mãn \({\left( {2x - 1} \right)^2} - {\left( {5x - 5} \right)^2} = 0\)

Phương pháp

Sử dụng công thức \({A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right)\) để đưa về dạng tìm \(x\) thường gặp

Lời giải

Ta có \({\left( {2x - 1} \right)^2} - {\left( {5x - 5} \right)^2} = 0\)\( \Leftrightarrow \left( {2x - 1 + 5x - 5} \right)\left( {2x - 1 - 5x + 5} \right) = 0\)\( \Leftrightarrow \left( {7x - 6} \right)\left( {4 - 3x} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{7x - 6 = 0}\\{4 - 3x = 0}\end{array}} \right.\)

\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{6}{7}}\\{x = \frac{4}{3}}\end{array}} \right.\)

Vậy có hai giá trị của \(x\) thỏa mãn yêu cầu.

Đáp án C.

Câu 5: Chọn câu đúng.

Phương pháp

Sử dụng công thức lập phương của một tổng \({\left( {A + B} \right)^3}\)\( = {A^3} + 3{A^2}B + 3A{B^2} + {B^3}\) và lập phương của một hiệu

\({\left( {A - B} \right)^3}\)\( = {A^3} - 3{A^2}B + 3A{B^2} - {B^3}\)

Lời giải

Ta có \(8 + 12y + 6{y^2} + {y^3}\)\( = {2^3} + {3.2^2}y + 3.2.{y^2} + {y^3}\)\( = {\left( {2 + y} \right)^3} \ne \left( {8 + {y^3}} \right)\) nên A sai.

+ Xét  \({\left( {2x - y} \right)^3}\)\( = {\left( {2x} \right)^3} - 3.{\left( {2x} \right)^2}.y + 3.2x.{y^2} - {y^3}\)\( = 8{x^3} - 12{x^2}y + 6xy - {y^3}\)\( \ne 2{x^3} - 6{x^2}y + 6xy - {y^3}\) nên C sai.

+ Xét \({\left( {3a + 1} \right)^3}\)\( = {\left( {3a} \right)^3} + 3.{\left( {3a} \right)^2}.1 + 3.3a{.1^2} + 1\)\( = 27{a^3} + 27{a^2} + 9a + 1\)\( \ne 3{a^3} + 9{a^2} + 3a + 1\) nên D sai

Đáp án B.

Câu 6: Tứ giác ABCD có \(AB = BC,CD = DA,\;\hat B = {90^0};\;\hat D = {120^0}\). Hãy chọn câu đúng nhất:

Phương pháp

Ta sử dụng  tính chất tam giác vuông cân , tam giác cân và tổng ba góc trong tam giác bằng \({180^\circ }\) .

Lời giải

Xét tam giác ABC có \(\hat B = {90^\circ };AB = BC \Rightarrow \Delta ABC\) vuông cân \( \Rightarrow \widehat {BAC} = \widehat {BCA} = \frac{{{{90}^\circ }}}{2} = {45^\circ }\)

Xét tam giác ADC có \(CD = DA \Rightarrow \Delta ADC\) cân tại \(D\) có \(\widehat {ADC} = {120^\circ }\) nên \(\widehat {DAC} = \widehat {DCA} = \frac{{{{180}^\circ }{\rm{\;}} - {{120}^\circ }}}{2} = {30^\circ }\)

Từ đó ta có \(\hat A = \widehat {BAD} = \widehat {BAC} + \widehat {CAD} = {45^\circ }{\rm{\;}} + {30^\circ }{\rm{\;}} = {75^\circ }\)

Và \(\hat C = \widehat {BCD} = \widehat {BCA} + \widehat {ACD} = {45^\circ }{\rm{\;}} + {30^\circ }{\rm{\;}} = {75^\circ }\)

Nên \(\hat A = \hat C = {75^\circ }\) .

Đáp án D.

Câu 7: Hình thang ABCD (AB//CD) có số đo góc D bằng \({70^0},\)  số đo góc \(A\) là:

Phương pháp

Ta sử dụng tính chất của hình thang: Ta thấy góc \(A\) và \(D\) là hai góc trong cùng phía nên \(\hat A + \hat D = {180^0}\) từ đó ta suy ra số đo góc A.

Lời giải

\(\hat A + \hat D = {180^0}\)

\(\begin{array}{*{20}{l}}{ \Rightarrow \hat A = {{180}^0} - \hat D}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu}  = {{180}^0} - {{70}^0}}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu}  = {{110}^0}}\end{array}\)

Đáp án C.

Câu 8: Cho hình chóp tam giác đều có độ dài cạnh đáy là 5cm, độ dài trung đoạn của hình chóp là 6cm. Diện tích xung quanh của hình chóp tam giác đều đó là:

Phương pháp

Dựa vào công thức tính diện tích xung quanh của hình chóp tam giác đều.

Lời giải

Diện tích xung quanh hình chóp là:

\({S_{xq}} = p.d = \frac{{5 \times 3}}{2}.6 = \frac{{15}}{2}.6 = 45\;\left( {c{m^3}} \right)\)

Vậy diện tích xung quanh hình chóp tam giác đều có đó là 45 cm³.

Đáp án C.

Câu 9: Hình chóp tứ giác đều có mặt bên là hình gì?

Phương pháp

Dựa vào đặc điểm của hình chóp tứ giác.

Lời giải

Hình chóp tứ giác đều có mặt bên là hình tam giác cân.

Đáp án A.

Câu 10: Trong các hình vẽ bên dưới hình nào có thể gấp theo nét đứt để được hình chóp tứ giác đều: 

Phương pháp

Dựa vào đặc điểm của hình chóp tứ giác.

Lời giải

Trong các hình trên, chỉ có hình c có thể tạo được hình chóp tứ giác đều.

Đáp án B.

Câu 11: Cho \(\Delta\)ABC vuông tại A có AB = 4 cm, BC = 5 cm . Diện tích DABC bằng:

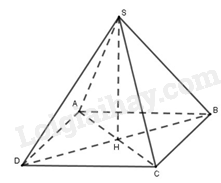
Phương pháp

Áp dụng định lí Pythagore để tính AC.

Sử dụng công thức tính diện tích tam giác để tính diện tích tam giác ABC.

Lời giải

Áp dụng định lí Pythagore vào tam giác ABC vuông tại A, ta có:

\(\begin{array}{l}A{B^2} + A{C^2} = B{C^2}\\{4^2} + A{C^2} = {5^2}\\A{C^2} = {5^2} - {4^2}\\A{C^2} = 9 = {3^2}\\ \Rightarrow AC = 3\end{array}\)

Diện tích tam giác ABC là:

\({S_{\Delta ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.3.4 = 6\left( {c{m^2}} \right)\)

Đáp án A.

Câu 12: Cho hình chóp S.ABCD đều có thể tích bằng 200cm³ , chiều cao SO bằng 12cm. Độ dài cạnh bên của hình chóp tứ giác đó là :

Phương pháp

Áp dụng công thức tính thể tích hình chóp tứ giác và định lí Pythagore để tính độ dài cạnh bên của hình chóp.

Lời giải

Ta có: \(V = \frac{1}{3}SO.{S_{ABCD}}\)

\(\begin{array}{l} \Leftrightarrow 200 = \frac{1}{3}.12.{S_{ABCD}}\\ \Rightarrow {S_{ABCD}} = \frac{{200}}{{\frac{1}{3}.12}} = \frac{{200}}{4} = 50\\ \Leftrightarrow B{C^2} = 50\end{array}\)

Tam giác BHC vuông cân nên HB² + HC² = BC² hay 2HC² = BC² hay 2HC² = 50

Suy ra HC² = 25

SC² = SH² + HC² = 12² + 25² = 169 = 13².

Vậy độ dài cạnh bên là 13cm.

Đáp án B.

Phần tự luận.

Bài 1. (2 điểm) Cho biểu thức: \(A = 3x(2x - y) + (x - y)(x + y) - 7{x^2} + {y^2}\).

a) Thu gọn A.

b) Tính giá trị của A biết x = \(\frac{{ - 2}}{3}\) và y = 2

Phương pháp

a) Sử dụng quy tắc cộng, trừ, nhân, chia đa thức và những hằng đẳng thức đáng nhớ để rút gọn.

b) Thay x, y vào A để tính giá trị.

Lời giải

a) \(A = 3x(2x - y) + (x - y)(x + y) - 7{x^2} + {y^2}\)

\( = 6{x^2} - 3xy + {x^2} - {y^2} - 7{x^2} + {y^2} =  - 3xy\)

b) Thay x = \(\frac{{ - 2}}{3}\) và y = 2 vào A, ta được: \(A =  - 3.\left( {\frac{{ - 2}}{3}} \right).2 = 4\).

Vậy A = -3xy, giá trị của A tại x = \(\frac{{ - 2}}{3}\) và y = 2 là 4.

Bài 2. (1,5 điểm) Tìm x biết:

a) \({\left( {x - 3} \right)^2} - {x^2} = 0\)

b) \({x^3} - 5{x^2} - 9x + 45 = 0\)

c) \(\left( {5x - 3} \right)\left( {2x + 1} \right) - {\left( {2x - 1} \right)^2} + 4 = 0\)

Phương pháp

Dựa vào các hằng đẳng thức đáng nhớ, phân tích đa thức thành nhân tử để tìm x.

Lời giải

a) \({\left( {x - 3} \right)^2} - {x^2} = 0\)

\(\begin{array}{l}(x - 3 - x)(x - 3 + x) = 0\\ - 3.(2x - 3) = 0\\2x - 3 = 0\\x = \frac{3}{2}\end{array}\)

Vậy \(x = \frac{3}{2}\)

b) \({x^3} - 5{x^2} - 9x + 45 = 0\)

\(\begin{array}{l}{x^2}(x - 5) - 9(x - 5) = 0\\({x^2} - 9)(x - 5) = 0\\(x - 3)(x + 3)(x - 5) = 0\\\left[ \begin{array}{l}x - 3 = 0\\x + 3 = 0\\x - 5 = 0\end{array} \right.\\\left[ \begin{array}{l}x = 3\\x =  - 3\\x = 5\end{array} \right.\end{array}\)

Vậy x =3, x = -3 hoặc x = 5.

c) \(\left( {5x - 3} \right)\left( {2x + 1} \right) - {\left( {2x - 1} \right)^2} + 4 = 0\)

\(\begin{array}{l}\left( {5x - 3} \right)\left( {2x + 1} \right) - {\left( {2x - 1} \right)^2} + 4 = 0\\\left( {5x - 3} \right)\left( {2x + 1} \right) - \left[ {\left( {2x - 1} \right) - 4} \right] = 0\\\left( {5x - 3} \right)\left( {2x + 1} \right) - \left( {2x - 1 - 2} \right)\left( {2x - 1 + 2} \right) = 0\\\left( {5x - 3} \right)\left( {2x + 1} \right) - \left( {2x - 3} \right)\left( {2x + 1} \right) = 0\\\left( {5x - 3 - 2x + 3} \right)\left( {2x + 1} \right) = 0\\3x\left( {2x + 1} \right) = 0\\\left[ \begin{array}{l}x = 0\\2x + 1 = 0\end{array} \right.\\\left[ \begin{array}{l}x = 0\\x =  - \frac{1}{2}\end{array} \right.\end{array}\)

Vậy x = 0 hoặc x = \( - \frac{1}{2}\).

Bài 3. (1 điểm) Người ta thiết kế chậu trồng cây có dạng hình chóp tam giác đều (như hình vẽ bên) biết: cạnh đáy khoảng 20cm, chiều cao khoảng 35 cm, độ dài trung đoạn khoảng 21 cm.

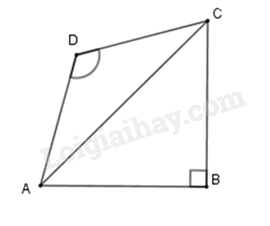
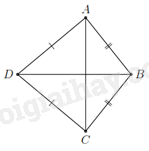
a) Người ta muốn sơn các bề mặt xung quanh chậu . Hỏi diện tích bề mặt cần sơn là bao nhiêu?

b) Tính thể tích của chậu trồng cây đó (làm tròn kết quả đến hàng phần trăm). Biết đường cao của mặt đáy hình chóp là 17cm .

Phương pháp

a) Sử dụng công thức tính diện tích xung quanh hình chóp tam giác.

b) Tính thể tích hình chóp tam giác.

Lời giải

a) Diện tích bề mặt cần sơn là :

              \({S_{xq}} = \frac{1}{2}.C.d = \frac{1}{2}.(3.20).21 = 630(c{m^2})\)

b) Thể tích của chậu trồng cây đó là :

             \(V = \frac{1}{3}.S.h = \frac{1}{3}.(\frac{1}{2}.20.17).35 = 1983,33(c{m^3})\)

Bài 4. (2 điểm)

1. Cho tứ giác \(ABCD\) có \(AB = BC\); \(CD = DA\). Biết \(\hat B = {100^\circ }\), \(\hat D = {80^\circ }\). Tính \(\hat A\) và \(\hat C\).

2. Tính chiều dài đường trượt AC trong hình vẽ trên (kết quả làm tròn hàng phần mười).

Phương pháp

a) Chứng minh \(\Delta\)ABD = \(\Delta\)CBD => $\hat{A}=\hat{C}$.

Áp dụng định lí tổng các góc của hình tứ giác bằng 360⁰ để tính \(\hat A\) và \(\hat C\).

b) Áp dụng định lí Pythagore trong tam giác vuông AHB, AHC để tính AC.

Lời giải

1.

1. Xét \(\Delta\)ABD và \(\Delta\)CBD có

$AB=AC$ (giả thiết);

$AD=DC$ (giả thiết);

$BD$là cạnh chung.

$\Rightarrow $ \(\Delta\)ABD = \(\Delta\)CBD (c.c.c), suy ra $\hat{A}=\hat{C}$.

Vậy \(\hat A + \hat B + \hat C + \hat D = {360^\circ } \Rightarrow \hat A = \hat C = {90^\circ }\).

2.

Áp dụng định lý Pythagore trong tam giác AHB vuông tại H.

                \(\begin{array}{l}A{B^2} = A{H^2} + H{B^2}\\ \Rightarrow H{B^2} = A{B^2} - A{H^2} = {(5)^2} - {(3)^2} = 25 - 9 = 16\\ \Rightarrow HB = \sqrt {16}  = 4m\end{array}\)

                \( \Rightarrow CH = CB - HB = 10 - 4 = 6m\)

Áp dụng định lí Pythagore trong tam giác AHC vuông tại H.

              \(\begin{array}{l}A{C^2} = A{H^2} + C{H^2} = {(3)^2} + {(6)^2} = 9 + 36 = 45\\ \Rightarrow AC = \sqrt {45}  \approx 6,7m\end{array}\)

Vậy chiều dài đường trượt AC là 6,7m.

Bài 4. (0,5 điểm) Cho a + b + c. Chứng minh \({a^3} + {b^3} + {c^3} = 3abc\).

Phương pháp

Dựa vào hằng đẳng thức \({\left( {a + b} \right)^3} = {a^3} + 3{a^2}b + 3a{b^2} + {b^3}\) để suy ra \({(a + b + c)^3}\). Thay a + b + c = 0 để chứng minh.

Lời giải

Vì \(a + b + c = 0\) nên \({\left( {a + b + c} \right)^3} = 0\).

Phân tích \({\left( {a + b + c} \right)^3}\) ta được \({\left( {a + b + c} \right)^3} = {a^3} + {b^3} + {c^3} + 3{a^2}b + 3a{b^2} + 3{b^2}c + 3b{c^2} + 3{a^2}c + 3a{c^2} + 6abc\)

\( =  > {a^3} + {b^3} + {c^3} + 3{a^2}b + 3a{b^2} + 3{b^2}c + 3b{c^2} + 3{a^2}c + 3a{c^2} + 6abc = 0\)

\( =  > {a^3} + {b^3} + {c^3} + \left( {3{a^2}b + 3a{b^2} + 3abc} \right) + \left( {3{b^2}c + 3b{c^2} + 3abc} \right) + \left( {3{a^2}c + 3a{c^2} + 3abc} \right) - 3abc = 0\)

\( =  > {a^3} + {b^3} + {c^3} + 3ab\left( {a + b + c} \right) + 3bc\left( {a + b + c} \right) + 3ac\left( {a + b + c} \right) = 3abc\)

\(Do{\rm{ }}a + b + c = 0\)

\( =  > {a^3} + {b^3} + {c^3} = 3abc\) (đpcm).