Đề thi học kì 1 Toán 11 Cánh diều - Đề số 3Tổng hợp đề thi học kì 2 lớp 11 tất cả các môn - Cánh diều Toán - Văn - Anh - Lí - Hóa - Sinh Phần trắc nghiệm (6 điểm) Câu 1: Chọn đáp án đúngĐề bài
I. Trắc nghiệm
Câu 1 :
Xét góc lượng giác \(\left( {OA,OM} \right) = \alpha \), trong đó M là điểm không nằm trên các trục tọa độ Ox và Oy. Khi đó, M thuộc góc phần tư nào để \(\sin \alpha \) và \(\cos \alpha \) trái dấu?
Câu 2 :
Cho \({90^0} < \alpha < {180^0}\). Chọn khẳng định đúng:
Câu 3 :
Trong các giá trị sau, \(\sin \alpha \) không thể nhận giá trị nào?
Câu 4 :
Chọn phát biểu đúng:
Câu 5 :
Tập xác định của hàm số \(y = 2\sin x\) là:
Câu 6 :
Chọn khẳng định đúng:
Câu 7 :
Dãy số \(\left( {{u_n}} \right)\) gồm các số nguyên dương chia hết cho 5. Số nào dưới đây thuộc dãy số \(\left( {{u_n}} \right)\)?
Câu 8 :
Cấp số cộng nào dưới đây có công sai bằng 3?
Câu 9 :
Cho dãy số \(\left( {{u_n}} \right)\) thỏa mãn \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = 2\). Tính \(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - 6} \right)\)
Câu 10 :
Phát biểu nào sau đây là sai?
Câu 11 :
Giả sử hai hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) liên tục tại điểm \({x_o}\). Hàm số \(y = \frac{{f\left( x \right)}}{{g\left( x \right)}}\) liên tục tại điểm \({x_o}\) nếu:
Câu 12 :
Giá trị của \(\mathop {\lim }\limits_{x \to + \infty } {x^5}\) là:
Câu 13 :
Một mặt phẳng được xác định nếu mặt phẳng đó chứa:
Câu 14 :
Cho hình chóp S. ABCD với ABCD là hình bình hành. Hai điểm S và B cùng thuộc hai mặt phẳng:
Câu 15 :
Trong các mệnh đề sau, mệnh đề nào đúng?
Câu 16 :
Cho hình hộp ABCD. A’B’C’D’. Hình hộp đó có bao nhiêu mặt bên?
Câu 17 :
Khẳng định nào sau đây là sai?
Câu 18 :
Qua phép chiếu song song, tính chất nào không được bảo toàn?
Câu 19 :
Biết rằng \(\tan \alpha = 2\). Giá trị biểu thức \(\frac{{\sin \alpha + 2\cos \alpha }}{{3\sin \alpha - \cos \alpha }}\) \(\left( {\cos \alpha \ne 0} \right)\)là:
Câu 20 :
Cho tam giác ABC. Chọn đáp án đúng:
Câu 21 :
Tập xác định của hàm số \(y = \frac{{2\sin x}}{{\sin x - \cos x}}\) là:
Câu 22 :
Cho dãy số \(\left( {{u_n}} \right)\) có số hạng tổng quát \({u_n} = \frac{{2n + 1}}{{n + 2}}\). Số \(\frac{{167}}{{84}}\) là số hạng thứ bao nhiêu của dãy số?
Câu 23 :
Cho \(\left( {{u_n}} \right)\) là cấp số cộng thỏa mãn \({u_2} = 8;{u_4} = 12\). Số hạng đầu của cấp số cộng bằng:
Câu 24 :
Tính tổng \(S = 1 + \frac{1}{2} + \frac{1}{4} + ... + \frac{1}{{{2^9}}}\)
Câu 25 :
Kết quả của giới hạn \(\mathop {\lim }\limits_{x \to - \infty } \left( {3{x^4} - 2{x^2} - 1} \right)\) bằng:
Câu 26 :
Chọn đáp án đúng:
Câu 27 :
Cho hàm số \(f\left( x \right) = \frac{{2x + 1}}{{{x^3} - x}}\). Kết luận nào sau đây là đúng?
Câu 28 :
Cho hình chóp tứ giác S. ABCD có BD và AC cắt nhau tại O. Trên SC lấy M không trùng với S và C, đường thẳng AM cắt SO tại K. Đường thẳng SD cắt đường thẳng nào?
Câu 29 :
Cho hình chóp S. ABCD có đáy là hình thang (AD// CB, \(BC < AD\)). Gọi M, N lần lượt là trung điểm của SA và SD. Khẳng định nào sau đây là đúng?
Câu 30 :
Cho hình chóp S. ABCD có đáy ABCD là hình thang (AB//CD). Gọi O là giao điểm của AC và BD, I là giao điểm của AD và BC. Giao tuyến của hai mặt phẳng (SAC) và (SBD) là:
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Câu 1 :
Xét góc lượng giác \(\left( {OA,OM} \right) = \alpha \), trong đó M là điểm không nằm trên các trục tọa độ Ox và Oy. Khi đó, M thuộc góc phần tư nào để \(\sin \alpha \) và \(\cos \alpha \) trái dấu?
Đáp án : C Phương pháp giải :
Sử dụng kiến thức về dấu của các giá trị lượng giác. Với \(\alpha \in \) góc phần tư thứ I thì: \(\sin \alpha > 0,\cos \alpha > 0\) Với \(\alpha \in \) góc phần tư thứ II thì: \(\sin \alpha > 0,\cos \alpha < 0\) Với \(\alpha \in \) góc phần tư thứ III thì: \(\sin \alpha < 0,\cos \alpha < 0\) Với \(\alpha \in \) góc phần tư thứ IV thì: \(\sin \alpha < 0,\cos \alpha > 0\) Lời giải chi tiết :
Ta có: Với \(\alpha \in \) góc phần tư thứ I thì: \(\sin \alpha > 0,\cos \alpha > 0\) Với \(\alpha \in \) góc phần tư thứ II thì: \(\sin \alpha > 0,\cos \alpha < 0\) Với \(\alpha \in \) góc phần tư thứ III thì: \(\sin \alpha < 0,\cos \alpha < 0\) Với \(\alpha \in \) góc phần tư thứ IV thì: \(\sin \alpha < 0,\cos \alpha > 0\) Do đó, M thuộc góc phần tư thứ (II) và (IV) thì \(\sin \alpha \) và \(\cos \alpha \) trái dấu.
Câu 2 :
Cho \({90^0} < \alpha < {180^0}\). Chọn khẳng định đúng:
Đáp án : A Phương pháp giải :
Sử dụng kiến thức về dấu của giá trị lượng giác: Với \({90^0} < \alpha < {180^0}\) thì \(\sin \alpha > 0\), \(\cos \alpha < 0,\tan \alpha < 0,\cot \alpha < 0\). Lời giải chi tiết :
Với \({90^0} < \alpha < {180^0}\) thì \(\sin \alpha > 0\), \(\cos \alpha < 0,\tan \alpha < 0,\cot \alpha < 0\).
Câu 3 :
Trong các giá trị sau, \(\sin \alpha \) không thể nhận giá trị nào?
Đáp án : B Phương pháp giải :
Sử dụng kiến thức về tập giá trị của hàm số \(y = \sin x\): \( - 1 \le \sin x \le 1\) Lời giải chi tiết :
Vì \( - 1 \le \sin \alpha \le 1\) nên \(\sin \alpha \) không thể nhận giá trị 1,2.
Câu 4 :
Chọn phát biểu đúng:
Đáp án : D Phương pháp giải :
Sử dụng kiến thức về hàm số chẵn: Hàm số \(y = f\left( x \right)\) với tập xác định D được gọi là hàm số chẵn nếu với mọi \(x \in D\) ta có \( - x \in D\) và \(f\left( { - x} \right) = f\left( x \right)\) Lời giải chi tiết :
Vì \(\cos \left( { - x} \right) = \cos x\) nên hàm số \(y = \cos x\) là hàm số chẵn.
Câu 5 :
Tập xác định của hàm số \(y = 2\sin x\) là:
Đáp án : C Phương pháp giải :
Sử kiến thức về tập xác định của hàm số \(y = \sin x\): Hàm số \(y = \sin x\) có tập xác định là \(\mathbb{R}\). Lời giải chi tiết :
Hàm số \(y = 2\sin x\) có tập xác định là \(\mathbb{R}\).
Câu 6 :
Chọn khẳng định đúng:
Đáp án : A Phương pháp giải :
Sử dụng kiến thức về dãy số giảm: Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số giảm nếu ta có: \({u_{n + 1}} < {u_n}\) với mọi \(n \in \mathbb{N}*\) Lời giải chi tiết :
Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số giảm nếu ta có: \({u_{n + 1}} < {u_n}\) với mọi \(n \in \mathbb{N}*\). Tức là: Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số giảm nếu ta có: \({u_{n + 1}} - {u_n} < 0\) với mọi \(n \in \mathbb{N}*\).
Câu 7 :
Dãy số \(\left( {{u_n}} \right)\) gồm các số nguyên dương chia hết cho 5. Số nào dưới đây thuộc dãy số \(\left( {{u_n}} \right)\)?
Đáp án : C Phương pháp giải :
Sử dụng kiến thức về cách cho một dãy số bằng phương pháp mô tả. Lời giải chi tiết :
Vì \(5 \vdots 5\) nên 5 thuộc dãy số \(\left( {{u_n}} \right)\).
Câu 8 :
Cấp số cộng nào dưới đây có công sai bằng 3?
Đáp án : D Phương pháp giải :
Sử dụng kiến thức về cấp số cộng: Cấp số cộng là một dãy số (hữu hạn hay vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi d. Lời giải chi tiết :
Xét dãy số: 0; 3; 6; 9; … ta thấy: Kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với 3 nên dãy số 0; 3; 6; 9; … có công sai bằng 3.
Câu 9 :
Cho dãy số \(\left( {{u_n}} \right)\) thỏa mãn \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = 2\). Tính \(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - 6} \right)\)
Đáp án : B Phương pháp giải :
Sử dụng quy tắc về giới hạn dãy số: Nếu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a,\mathop {\lim }\limits_{n \to + \infty } {v_n} = b\) thì \(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} + {v_n}} \right) = a + b\). Lời giải chi tiết :
\(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - 6} \right) = 2 - 6 = - 4\)
Câu 10 :
Phát biểu nào sau đây là sai?
Đáp án : C Phương pháp giải :
Sử dụng kiến thức giới hạn dãy số: \(\mathop {\lim }\limits_{n \to + \infty } {q^n} = 0\left( {\left| q \right| < 1} \right)\) Lời giải chi tiết :
Vì \(\mathop {\lim }\limits_{n \to + \infty } {q^n} = 0\left( {\left| q \right| < 1} \right)\) nên C là câu sai.
Câu 11 :
Giả sử hai hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) liên tục tại điểm \({x_o}\). Hàm số \(y = \frac{{f\left( x \right)}}{{g\left( x \right)}}\) liên tục tại điểm \({x_o}\) nếu:
Đáp án : A Phương pháp giải :
Sử dụng kiến thức về tính chất cơ bản của hàm số liên tục: Giả sử hai hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) liên tục tại điểm \({x_o}\). Hàm số \(y = \frac{{f\left( x \right)}}{{g\left( x \right)}}\) liên tục tại điểm \({x_o}\) nếu \(g\left( {{x_0}} \right) \ne 0\). Lời giải chi tiết :
Giả sử hai hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) liên tục tại điểm \({x_o}\). Hàm số \(y = \frac{{f\left( x \right)}}{{g\left( x \right)}}\) liên tục tại điểm \({x_o}\) nếu \(g\left( {{x_0}} \right) \ne 0\).
Câu 12 :
Giá trị của \(\mathop {\lim }\limits_{x \to + \infty } {x^5}\) là:
Đáp án : D Phương pháp giải :
Sử dụng quy tắc tính giới hạn của hàm số: \(\mathop {\lim }\limits_{x \to + \infty } {x^k} = + \infty \) với k là số nguyên dương. Lời giải chi tiết :
\(\mathop {\lim }\limits_{x \to + \infty } {x^5} = + \infty \)
Câu 13 :
Một mặt phẳng được xác định nếu mặt phẳng đó chứa:
Đáp án : C Phương pháp giải :
Sử dụng kiến thức về cách xác định một mặt phẳng: Một mặt phẳng hoàn toàn được xác định khi chứa hai đường thẳng cắt nhau. Lời giải chi tiết :
Một mặt phẳng hoàn toàn được xác định khi chứa hai đường thẳng cắt nhau.
Câu 14 :
Cho hình chóp S. ABCD với ABCD là hình bình hành. Hai điểm S và B cùng thuộc hai mặt phẳng:
Đáp án : B Phương pháp giải :
Sử dụng kiến thức điểm thuộc mặt phẳng. Lời giải chi tiết :
Hai điểm S và B cùng thuộc 2 mặt phẳng (SAB) và (SBD).
Câu 15 :
Trong các mệnh đề sau, mệnh đề nào đúng?
Đáp án : C Phương pháp giải :
Sử dụng kiến thức về vị trí hai đường thẳng song song. Lời giải chi tiết :
Hai đường thẳng không có điểm chung là hai đường thẳng song song hoặc chéo nhau.
Câu 16 :
Cho hình hộp ABCD. A’B’C’D’. Hình hộp đó có bao nhiêu mặt bên?
Đáp án : C Phương pháp giải :
Sử dụng kiến thức về hình hộp: Hình hộp ABCD. A’B’C’D’ có bốn mặt bên là ABB’A’, BCC’B’, CDD’C’, ADD’A’. Lời giải chi tiết :
Hình hộp ABCD. A’B’C’D’ có bốn mặt bên là ABB’A’, BCC’B’, CDD’C’, ADD’A’.
Câu 17 :
Khẳng định nào sau đây là sai?
Đáp án : D Phương pháp giải :
Sử dụng kiến thức về hình lăng trụ. Lời giải chi tiết :
Trong hình lăng trụ, các mặt bên có thể không bằng nhau. Ví dụ: Hình lăng trụ dưới đây có các mặt bên không bằng nhau
Câu 18 :
Qua phép chiếu song song, tính chất nào không được bảo toàn?
Đáp án : C Phương pháp giải :
Sử dụng kiến thức về phép chiếu song song. Lời giải chi tiết :
Qua phép chiếu song song, tính chất chéo nhau không được bảo toàn.
Câu 19 :
Biết rằng \(\tan \alpha = 2\). Giá trị biểu thức \(\frac{{\sin \alpha + 2\cos \alpha }}{{3\sin \alpha - \cos \alpha }}\) \(\left( {\cos \alpha \ne 0} \right)\)là:
Đáp án : A Phương pháp giải :
Sử dụng công thức: \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\). Lời giải chi tiết :
\(\frac{{\sin \alpha + 2\cos \alpha }}{{3\sin \alpha - \cos \alpha }} = \frac{{\frac{{\sin \alpha }}{{\cos \alpha }} + \frac{{2\cos \alpha }}{{\cos \alpha }}}}{{\frac{{3\sin \alpha }}{{\cos \alpha }} - \frac{{\cos \alpha }}{{\cos \alpha }}}} = \frac{{\tan \alpha + 2}}{{3\tan \alpha - 1}} = \frac{{2 + 2}}{{3.2 - 1}} = \frac{4}{5}\)
Câu 20 :
Cho tam giác ABC. Chọn đáp án đúng:
Đáp án : A Phương pháp giải :
Sử dụng công thức \(\sin \left( {\frac{\pi }{2} - \alpha } \right) = \cos \alpha \) Lời giải chi tiết :
Vì \(\widehat A + \widehat B + \widehat C = \pi \Rightarrow \frac{{\widehat A + \widehat B}}{2} = \frac{\pi }{2} - \frac{{\widehat C}}{2}\). Do đó: \(\sin \frac{{A + B}}{2} = \sin \left( {\frac{\pi }{2} - \frac{C}{2}} \right) = \cos \frac{C}{2}\)
Câu 21 :
Tập xác định của hàm số \(y = \frac{{2\sin x}}{{\sin x - \cos x}}\) là:
Đáp án : C Phương pháp giải :
Sử dụng kiến thức về tập xác định của hàm số: Hàm phân thức xác định khi mẫu thức khác 0. Lời giải chi tiết :
Hàm số \(y = \frac{{2\sin x}}{{\sin x - \cos x}}\) xác định khi \(\sin x - \cos x \ne 0 \Leftrightarrow \sin \left( {x - \frac{\pi }{4}} \right) \ne 0 \Leftrightarrow x \ne \frac{\pi }{4} + k\pi ,k \in \mathbb{Z}\)
Câu 22 :
Cho dãy số \(\left( {{u_n}} \right)\) có số hạng tổng quát \({u_n} = \frac{{2n + 1}}{{n + 2}}\). Số \(\frac{{167}}{{84}}\) là số hạng thứ bao nhiêu của dãy số?
Đáp án : B Phương pháp giải :
Thay \({u_n} = \frac{{167}}{{84}}\) vào số hạng tổng quát rồi tìm n. Lời giải chi tiết :
Ta có: \(\frac{{167}}{{84}} = \frac{{2n + 1}}{{n + 2}} \Leftrightarrow 84\left( {2n + 1} \right) = 167\left( {n + 2} \right) \Leftrightarrow 168n + 84 = 167n + 334 \Leftrightarrow n = 250\) Do đó, số \(\frac{{167}}{{84}}\) là số hạng thứ 250 của dãy số.
Câu 23 :
Cho \(\left( {{u_n}} \right)\) là cấp số cộng thỏa mãn \({u_2} = 8;{u_4} = 12\). Số hạng đầu của cấp số cộng bằng:
Đáp án : A Phương pháp giải :
Sử dụng kiến thức về công thức số hạng tổng quát của cấp số cộng: Cho cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công sai d thì số hạng tổng quát \({u_n}\) của nó được xác định theo công thức: \({u_n} = {u_1} + \left( {n - 1} \right)d\). Lời giải chi tiết :
Theo đầu bài ta có hệ phương trình: \(\left\{ \begin{array}{l}{u_2} = {u_1} + d\\{u_4} = {u_1} + 3d\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}8 = {u_1} + d\\12 = {u_1} + 3d\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1} = 6\\d = 2\end{array} \right.\) Vậy số hạng đầu tiên của cấp số cộng là \({u_1} = 6\).
Câu 24 :
Tính tổng \(S = 1 + \frac{1}{2} + \frac{1}{4} + ... + \frac{1}{{{2^9}}}\)
Đáp án : D Phương pháp giải :
Sử dụng kiến thức về công thức tổng của n số hạng đầu của cấp số nhân: Cho cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công bội \(q \ne 1\) thì \(S = {u_1} + {u_2} + ... + {u_n} = \frac{{{u_1}\left( {1 - {q^n}} \right)}}{{1 - q}}\) Lời giải chi tiết :
Cấp số nhân trên có số hạng đầu \({u_1} = 1\), công bội \(q = \frac{1}{2}\). Do đó: \(S = \frac{{1.\left[ {1 - {{\left( {\frac{1}{2}} \right)}^{10}}} \right]}}{{1 - \frac{1}{2}}} = \frac{{1\;023}}{{512}}\)
Câu 25 :
Kết quả của giới hạn \(\mathop {\lim }\limits_{x \to - \infty } \left( {3{x^4} - 2{x^2} - 1} \right)\) bằng:
Đáp án : D Phương pháp giải :
Sử dụng kiến thức giới hạn hàm số: Nếu \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = + \infty \), \(\mathop {\lim }\limits_{x \to - \infty } g\left( x \right) = L > 0\) thì \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right).g\left( x \right)} \right] = + \infty \). Lời giải chi tiết :
Ta có: \(\mathop {\lim }\limits_{x \to - \infty } \left( {3{x^4} - 2{x^2} - 1} \right) = \mathop {\lim }\limits_{x \to - \infty } {x^4}\left( {3 - \frac{2}{{{x^2}}} - \frac{1}{{{x^4}}}} \right)\) Vì \(\mathop {\lim }\limits_{x \to - \infty } {x^4} = + \infty \) và \(\mathop {\lim }\limits_{x \to - \infty } \left( {3 - \frac{2}{{{x^2}}} - \frac{1}{{{x^4}}}} \right) = 3 > 0\) nên \(\mathop {\lim }\limits_{x \to - \infty } {x^4}\left( {3 - \frac{2}{{{x^2}}} - \frac{1}{{{x^4}}}} \right) = + \infty \)
Câu 26 :
Chọn đáp án đúng:
Đáp án : A Phương pháp giải :
Sử dụng quy tắc về giới hạn của dãy số: Nếu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a,\mathop {\lim }\limits_{n \to + \infty } {v_n} = b \ne 0\) thì \(\mathop {\lim }\limits_{n \to + \infty } \frac{{{u_n}}}{{{v_n}}} = \frac{a}{b}\). Lời giải chi tiết :
\(\mathop {\lim }\limits_{n \to + \infty } \frac{{{3^n} - {2^n}}}{{{{4.3}^n} + {2^n}}} = \mathop {\lim }\limits_{n \to + \infty } \frac{{1 - {{\left( {\frac{2}{3}} \right)}^n}}}{{4 + {{\left( {\frac{2}{3}} \right)}^n}}} = \frac{1}{4}\)
Câu 27 :
Cho hàm số \(f\left( x \right) = \frac{{2x + 1}}{{{x^3} - x}}\). Kết luận nào sau đây là đúng?
Đáp án : D Phương pháp giải :
Sử dụng kiến thức về tính liên tục của hàm số sơ cấp cơ bản: Hàm phân thức hữu tỉ (thương là hai đa thức) liên tục trên tập xác định của chúng. Lời giải chi tiết :
Hàm số f(x) xác định khi \({x^3} - x \ne 0 \Leftrightarrow x\left( {{x^2} - 1} \right) \ne 0 \Leftrightarrow \left\{ \begin{array}{l}x \ne 0\\x \ne \pm 1\end{array} \right.\) Do đó, hàm số f(x) liên tục trên các khoảng \(\left( { - \infty ; - 1} \right),\left( { - 1;0} \right),\left( {0;1} \right),\left( {1; + \infty } \right)\) Vậy hàm số liên tục tại \(x = \frac{1}{4}\)
Câu 28 :
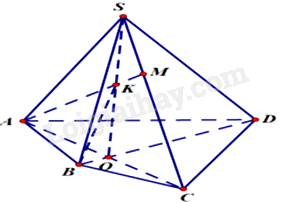
Cho hình chóp tứ giác S. ABCD có BD và AC cắt nhau tại O. Trên SC lấy M không trùng với S và C, đường thẳng AM cắt SO tại K. Đường thẳng SD cắt đường thẳng nào?
Đáp án : B Phương pháp giải :
Sử dụng kiến thức về hai đường thẳng cắt nhau. Lời giải chi tiết :
Vì hai đường thẳng SD và BK cùng nằm trong mặt phẳng (SBD) nên đường thẳng SD cắt đường thẳng BK.
Câu 29 :
Cho hình chóp S. ABCD có đáy là hình thang (AD// CB, \(BC < AD\)). Gọi M, N lần lượt là trung điểm của SA và SD. Khẳng định nào sau đây là đúng?
Đáp án : A Phương pháp giải :
Sử dụng kiến thức về tính chất của hai đường thẳng song song: Trong không gian, hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau. Lời giải chi tiết :
Vì M, N lần lượt là trung điểm của SA và SD nên MN là đường trung bình của tam giác SAD. Do đó, MN//AD. Mà AD// CB nên MN//BC
Câu 30 :
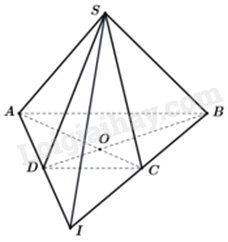
Cho hình chóp S. ABCD có đáy ABCD là hình thang (AB//CD). Gọi O là giao điểm của AC và BD, I là giao điểm của AD và BC. Giao tuyến của hai mặt phẳng (SAC) và (SBD) là:
Đáp án : B Phương pháp giải :
Sử dụng kiến thức về giao tuyến của hai mặt phẳng: Đường thẳng d (nếu có) của hai mặt phẳng phân biệt (P) và (Q) được gọi là giao tuyến của hai mặt phẳng đó và kí hiệu là \(d = \left( P \right) \cap \left( Q \right)\). Lời giải chi tiết :
Ta có: S là điểm chung của hai mặt phẳng (SAC) và (SBD). Vì O là giao điểm của AC và BD nên O là điểm chung của hai mặt phẳng (SAC) và (SBD). Vậy giao tuyến của hai mặt phẳng (SAC) và (SBD) là SO.
II. Tự luận
Phương pháp giải :
Sử dụng kiến thức về hàm số liên tục: Hàm số \(y = f\left( x \right)\) được gọi là liên tục trên khoảng \(\left( {a;b} \right)\) nếu nó liên tục tại mọi điểm thuộc khoảng này. Lời giải chi tiết :
Tập xác định: \(D = \mathbb{R}\) Khi \(x \in \left( { - \infty ;1} \right)\): Hàm số \(f\left( x \right) = mx + 3\) liên tục trên \(\left( { - \infty ;1} \right)\). Khi \(x \in \left( {1; + \infty } \right)\): Hàm số \(f\left( x \right) = \frac{1}{{x - 1}} - \frac{3}{{{x^3} - 1}}\) liên tục trên \(\left( {1; + \infty } \right)\). Tại \(x = 1\): \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {\frac{1}{{x - 1}} - \frac{3}{{{x^3} - 1}}} \right) = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{{x^2} + x + 1 - 3}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}} = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{{x^2} + x - 2}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}\) \( = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{\left( {x - 1} \right)\left( {x + 2} \right)}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}} = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{x + 2}}{{{x^2} + x + 1}} = \frac{3}{3} = 1\) \(\mathop {\lim }\limits_{x \to {1^ - }} \left( {mx + 3} \right) = m + 3\), \(f\left( 1 \right) = m + 3\) Hàm số f(x) liên tục trên \(\mathbb{R}\) \( \Leftrightarrow \) hàm số f(x) liên tục tại \(x = 1\)\( \Leftrightarrow \mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = f\left( 1 \right)\) Tức là: \(m + 3 = 1 \Leftrightarrow m = - 2\) Phương pháp giải :
Sử dụng kiến thức về giao tuyến của hai mặt phẳng: Nếu hai mặt phẳng chứa hai đường thẳng song song với nhau thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó. Lời giải chi tiết :
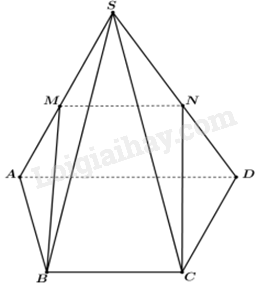
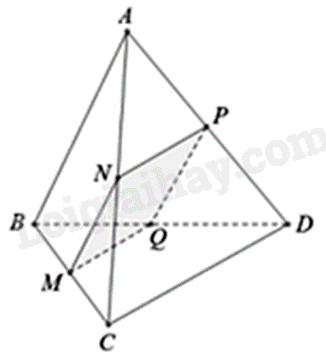
Vì (P) qua M và song song với AB nên \(\left( P \right) \cap \left( {ABC} \right) = MN\), với N là giao điểm của đường thẳng qua M song song với AB và cạnh AC. Vì (P) qua N và song song với CD nên \(\left( P \right) \cap \left( {ACD} \right) = NP\), với P là giao điểm của đường thẳng qua N song song với CD và cạnh AD. Vì (P) qua M và song song với CD nên \(\left( P \right) \cap \left( {BCD} \right) = MQ\), với Q là giao điểm của đường thẳng qua M song song với CD và cạnh BD. Do đó, thiết diện của tứ diện ABCD cắt bởi mặt phẳng (P) là tứ giác MNPQ. Ta có: MN//PQ, \(MN = PQ = \frac{1}{2}AB\), MQ//PN, \(MQ = PN = \frac{1}{2}DC\), \(AB = CD\) Do đó, \(MN = NP = PQ = QM\) nên tứ giác MNPQ là hình thoi. Phương pháp giải :
Sử dụng kiến thức công thức: \({\cos ^2}x + {\sin ^2}x = 1\) Lời giải chi tiết :
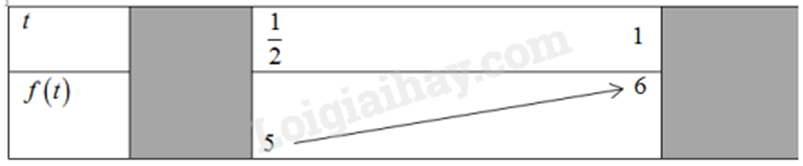
Ta có: \(y = 2{\cos ^2}x + 5\sin x + 1 = 2\left( {1 - {{\sin }^2}x} \right) + 5\sin x + 1 = - 2{\sin ^2}x + 5\sin x + 3\) (1) Đặt \(\sin x = t\). Vì \(x \in \left[ {\frac{\pi }{3};\frac{{5\pi }}{6}} \right]\) nên \(t \in \left[ {\frac{1}{2};1} \right]\). Thay \(\sin x = t\) vào (1) ta có: \(y = - 2{t^2} + 5t + 3\) với \(t \in \left[ {\frac{1}{2};1} \right]\) Ta có bảng:
Từ bảng ta có: Giá trị lớn nhất của hàm số đã cho trên \(\left[ {\frac{\pi }{3};\frac{{5\pi }}{6}} \right]\) là 6 khi \(t = 1\) hay \(x = \frac{\pi }{2}\) Giá trị nhỏ nhất của hàm số đã cho trên \(\left[ {\frac{\pi }{3};\frac{{5\pi }}{6}} \right]\) là 5 khi \(t = \frac{1}{2}\) hay \(x = \frac{{5\pi }}{6}\) Phương pháp giải :
Sử dụng kiến thức về công thức số hạng tổng quát của dãy số. Lời giải chi tiết :
Ta có: \({u_{n + 1}} = \frac{1}{3}\left( {2{u_n} + \frac{{n - 1}}{{{n^2} + 3n + 2}}} \right) = \frac{1}{3}\left( {2{u_n} + \frac{3}{{n + 2}} - \frac{2}{{n + 1}}} \right) = \frac{2}{3}{u_n} + \frac{1}{{n + 2}} - \frac{2}{3}.\frac{1}{{n + 1}}\) \( \Leftrightarrow {u_{n + 1}} - \frac{1}{{n + 2}} = \frac{2}{3}\left( {{u_n} - \frac{1}{{n + 1}}} \right)\) (1) Đặt \({v_n} = {u_n} - \frac{1}{{n + 1}}\), từ (1) suy ra \({v_{n + 1}} = \frac{2}{3}{v_n}\) Do đó, \(\left( {{v_n}} \right)\) là cấp số nhân với \({v_1} = {u_1} - \frac{1}{2} = \frac{1}{2}\), công bội \(q = \frac{2}{3}\) Suy ra: \({v_n} = {v_1}.{q^{n - 1}} = \frac{1}{2}{\left( {\frac{2}{3}} \right)^{n - 1}} \Leftrightarrow {u_n} - \frac{1}{{n + 1}} = \frac{1}{2}{\left( {\frac{2}{3}} \right)^{n - 1}} \Leftrightarrow {u_n} = \frac{1}{2}{\left( {\frac{2}{3}} \right)^{n - 1}} + \frac{1}{{n + 1}}\) Vậy \({u_{2020}} = \frac{1}{2}{\left( {\frac{2}{3}} \right)^{2019}} + \frac{1}{{2021}} = \frac{{{2^{2018}}}}{{{3^{2019}}}} + \frac{1}{{2021}}\)
|