Đề thi giữa kì 1 Toán 11 Cánh diều - Đề số 4Tải về Câu 1: Góc lượng giác nào dưới đây tương ứng với chuyển động quay (3frac{2}{5}) vòng ngược chiều kim đồng hồ? Tổng hợp đề thi học kì 2 lớp 11 tất cả các môn - Cánh diều Toán - Văn - Anh - Lí - Hóa - Sinh Đề bài Phần trắc nghiệm (5 điểm) Câu 1: Góc lượng giác nào dưới đây tương ứng với chuyển động quay \(3\frac{2}{5}\) vòng ngược chiều kim đồng hồ?
Câu 2: Chọn đáp án đúng:
Câu 3: Chọn khẳng định đúng:
Câu 4: Chọn đáp án đúng.
Câu 5: Huyết áp là áp lực cần thiết tác động lên thành của động mạch để đưa máu từ tim đến nuôi dưỡng các mô trong cơ thể. Huyết áp được tạo ra do lực co bóp của cơ tim và sức cản của thành động mạch. Mỗi lần tim đập, huyết áp của chúng ta tăng rồi giảm giữa các nhịp. Huyết áp tối đa và huyết áp tối thiểu tương ứng là huyết áp tâm thu và tâm trương. Chỉ số huyết áp 120/80 là bình thường. Giả sử huyết áp của một người nào đó được mô hình hóa bởi hàm số \(p\left( t \right) = 110 + 20\sin \left( {160\pi t} \right)\). Chọn đáp án đúng.
Câu 6: Sử dụng máy tính cầm tay để giải phương trình \(\sqrt 3 \tan x - 3 = 0\) với kết quả là radian (làm tròn kết quả đến hàng phần trăm) là:
Câu 7: Tìm tất cả các tham số thực m để phương trình \({\sin ^2}x + \sin x\cos x = m\) có nghiệm.
Câu 8: Dãy số có các số hạng đầu là \(0;\frac{1}{2};\frac{2}{3};\frac{3}{4};\frac{4}{5};...\) Số hạng tổng quát của dãy số này là:
Câu 9: Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + ... + \frac{1}{{{n^2}}},\forall n = 2;{\rm{ }}3;{\rm{ }}4; \cdots .\) Mệnh đề nào sau đây đúng?
Câu 10: Trong các dãy số được cho dưới đây, dãy số nào là cấp số cộng?
Câu 11: Một công ty thực hiện việc trả lương cho các kỹ sư theo phương thức sau: Mức lương của quý làm việc đầu tiên cho công ty là 14 triệu đồng/ quý và kể từ quý làm việc thứ hai, mức lương sẽ được tăng 500 000 đồng mỗi quý. Tổng số tiền một kỹ sư nhận được sau ba năm làm việc tại công ty là:
Câu 12: Cho ba góc của một tam giác lập thành một cấp số cộng, trong đó góc lớn nhất gấp đôi góc nhỏ nhất. Số đo góc lớn nhất của tam giác là:
Câu 13: Dãy số gồm các số tự nhiên lẻ nhỏ hơn 20, sắp xếp theo thứ tự từ bé đến lớn là:
Câu 14: Hình nào trong các hình sau đây là hình chóp tứ giác?
Câu 15: Cho tam giác ABC và điểm S không nằm trong mặt phẳng chứa tam giác ABC. Có bao nhiêu mặt phẳng được tạo thành?
Câu 16: Cho hình chóp S. ABCD có đáy ABCD là hình thang với AB là đáy lớn. Trên đoạn SA, lấy điểm I không trùng với S và A; trên đoạn BC lấy điểm J không trùng với B và C. Giao tuyến của đường thẳng IJ và mặt phẳng (SBD) là:
Câu 17: Cho hình chóp tam giác S. ABC. Trong các cặp đường thẳng sau, cặp đường thẳng nào không chéo nhau?
Câu 18: Cho tứ diện ABCD. Gọi I, J lần lượt là trọng tâm của các tam giác ABC và ABD. Gọi M, N lần lượt là trung điểm của BC và BD. Trong các đường thẳng MN, CD, BD, BC thì IJ song song với bao nhiêu đường thẳng?
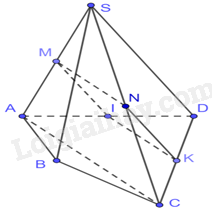
Câu 19: Cho hình chóp tứ giác S. ABCD có M, N, I, K lần lượt là trung điểm của SA, SC, AD, CD. Tứ giác MNKI là hình gì?
Câu 20: Cho các số a, b, c \(\left( {a < b < c,c \in \mathbb{Z}} \right)\) lập thành cấp số nhân; đồng thời \(a,b + 8,c\) theo thứ tự lập thành cấp số cộng và \(a,b + 8,c + 64\) theo thứ tự lập thành cấp số nhân. Giá trị biểu thức \(P = a + b + c\) là:
Phần tự luận (5 điểm) Bài 1. (1,5 điểm) 1) Giải các phương trình sau: a) \({\sin ^2}x - {\cos ^2}x + \cos 3x = 0\) b) \(\sin x + \sqrt 3 \cos x = 0\) 2) Tìm giá trị nhỏ nhất, lớn nhất của hàm số \(y = 2{\sin ^2}x + \sqrt 3 \sin 2x\) 3) Phương trình \({\tan ^4}x + 1 = \frac{{\left( {2 - {{\sin }^2}2x} \right)\sin 3x}}{{{{\cos }^4}x}}\) có bao nhiêu nghiệm thuộc \(\left( {\frac{\pi }{2};\pi } \right)\)? Bài 2. (1,5 điểm) a) Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = 4,{u_2} = 10.\) Tính \({u_{100}}\). b) Cho dãy số \(\left( {{u_n}} \right)\): \(\left( {{u_n}} \right):\left\{ \begin{array}{l}{u_1} = 3\\{u_{n + 1}} = \sqrt {1 + u_n^2} \end{array} \right.\). Tìm công thức số hạng tổng quát của dãy số trên. Bài 3. (1,0 điểm) Cho hình chóp S. ABCD có đáy là hình bình hành tâm O. Gọi M là trung điểm của SB. N là điểm trên cạnh BC sao cho \(BN = 2CN\). Xác định giao tuyến của mặt phẳng (SCD) và mặt phẳng (AMN). Bài 4. (1,0 điểm) a) Cho hình chóp S. ABCD có đáy là hình thang với đáy lớn là AB. Gọi I, J lần lượt là trung điểm của AD và BC và G là trọng tâm của tam giác SAB. Tìm giao tuyến của mặt phẳng (SAB) và mặt phẳng (IJG) b) Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi \({G_1},{G_2}\) lần lượt là trọng tâm các tam giác SAB và SCD. Gọi M, N lần lượt là trung điểm của AB, CD. Chứng minh rằng \({G_1}{G_2}\)//AD//BC -------- Hết -------- Lời giải chi tiết Phần trắc nghiệm (5 điểm)
Câu 1: Góc lượng giác nào dưới đây tương ứng với chuyển động quay \(3\frac{2}{5}\) vòng ngược chiều kim đồng hồ?
Phương pháp Một vòng quay của kim đồng hồ ứng với 360 độ, \({1^\circ } = \frac{\pi }{{180}}{\rm{ rad}} \) và \( 1{\rm{rad}} = {\left( {\frac{{180}}{\pi }} \right)^\circ }{\rm{. }}\) Quy ước chiều quay ngược với chiều kim đồng hồ là chiều dương. Lời giải \(3\frac{2}{5}\) vòng đường tròn ứng với: \(3\frac{2}{5}{.360^0} = 1\;{224^0} = \frac{{34\pi }}{5}rad\) Đáp án C Câu 2: Chọn đáp án đúng:
Phương pháp Sử dụng công thức: \(\tan \left( {\frac{\pi }{2} - \alpha } \right) = \cot \alpha ,\tan \alpha .\cot \alpha = 1,{\sin ^2}\alpha + {\cos ^2}\alpha = 1\) Lời giải Ta có: \(\sqrt {{{\sin }^4}x + 4{{\cos }^2}x} + \sqrt {{{\cos }^4}x + 4{{\sin }^2}x} = \sqrt {{{\sin }^4}x + 4\left( {1 - {{\sin }^2}x} \right)} + \sqrt {{{\cos }^4}x + 4\left( {1 - {{\cos }^2}x} \right)} \) \( = \sqrt {{{\left( {{{\sin }^2}x} \right)}^2} - 4{{\sin }^2}x + 4} + \sqrt {{{\left( {{{\cos }^2}x} \right)}^2} - 4{{\cos }^2}x + 4} = \sqrt {{{\left( {{{\sin }^2}x - 2} \right)}^2}} + \sqrt {{{\left( {{{\cos }^2}x - 2} \right)}^2}} \) \( = \left( {2 - {{\sin }^2}x} \right) + \left( {2 - {{\cos }^2}x} \right) = 4 - \left( {{{\sin }^2}x + {{\cos }^2}x} \right) = 3\) Lại có: \(\left( {x + \frac{\pi }{3}} \right) + \left( {\frac{\pi }{6} - x} \right) = \frac{\pi }{2} \Rightarrow \tan \left( {\frac{\pi }{6} - x} \right) = \cot \left( {x + \frac{\pi }{3}} \right) \Rightarrow \tan \left( {\frac{\pi }{6} - x} \right).\tan \left( {x + \frac{\pi }{3}} \right) = 1\) Do đó: \(\sqrt {{{\sin }^4}x + 4{{\cos }^2}x} + \sqrt {{{\cos }^4}x + 4{{\sin }^2}x} = 3\tan \left( {x + \frac{\pi }{3}} \right)\tan \left( {\frac{\pi }{6} - x} \right)\) Đáp án D Câu 3: Chọn khẳng định đúng:
Phương pháp Sử dụng công thức: \({\cos ^2}\alpha - {\sin ^2}\alpha = \cos 2\alpha ,{\cos ^2}\alpha + {\sin ^2}\alpha = 1\) Lời giải \({\sin ^4}\alpha - {\cos ^4}\alpha = {\left( {{{\sin }^2}\alpha } \right)^2} - {\left( {{{\cos }^2}\alpha } \right)^2} \\= \left( {{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right)\left( {{{\sin }^2}\alpha - {{\cos }^2}\alpha } \right) = {\sin ^2}\alpha - {\cos ^2}\alpha \\= - \cos 2\alpha \) Đáp án B Câu 4: Chọn đáp án đúng.
Phương pháp + Đồ thị hàm số chẵn nhận trục tung làm trục đối xứng. + Đồ thị hàm số lẻ nhận gốc tọa độ làm tâm đối xứng. Lời giải + Đồ thị hàm số chẵn nhận trục tung làm trục đối xứng. + Đồ thị hàm số lẻ nhận gốc tọa độ làm tâm đối xứng. Đáp án A Câu 5: Huyết áp là áp lực cần thiết tác động lên thành của động mạch để đưa máu từ tim đến nuôi dưỡng các mô trong cơ thể. Huyết áp được tạo ra do lực co bóp của cơ tim và sức cản của thành động mạch. Mỗi lần tim đập, huyết áp của chúng ta tăng rồi giảm giữa các nhịp. Huyết áp tối đa và huyết áp tối thiểu tương ứng là huyết áp tâm thu và tâm trương. Chỉ số huyết áp 120/80 là bình thường. Giả sử huyết áp của một người nào đó được mô hình hóa bởi hàm số \(p\left( t \right) = 110 + 20\sin \left( {160\pi t} \right)\). Chọn đáp án đúng.
Phương pháp Sử dụng kiến thức: \( - 1 \le \sin \alpha \le 1\) Lời giải Ta có: \( - 1 \le \sin \left( {160\pi t} \right) \le 1\forall t \in \mathbb{R} \Leftrightarrow - 20 \le 20\sin \left( {160\pi t} \right) \le 20\forall t \in \mathbb{R}\) \( \Leftrightarrow 90 \le 110 + 20\sin \left( {160\pi t} \right) \le 130\;\forall t \in \mathbb{R}\) Vậy chỉ số huyết áp của người này là 130/90 và chỉ số huyết áp của người này là cao hơn mức bình thường. Đáp án A Câu 6: Sử dụng máy tính cầm tay để giải phương trình \(\sqrt 3 \tan x - 3 = 0\) với kết quả là radian (làm tròn kết quả đến hàng phần trăm) là:
Phương pháp Sử dụng máy tính cầm tay để tìm nghiệm của phương trình. Lời giải Ta có: \(\sqrt 3 \tan x - 3 = 0 \Leftrightarrow \tan x = \sqrt 3 \) Sau khi chuyển máy tính sang chế độ “radian”. Bấm liên tiếp Ta được kết quả gần đúng là 1,05. Vậy phương trình \(\sqrt 3 \tan x - 3 = 0\) có các nghiệm là \(x \approx 1,05 + k\pi ,k \in \mathbb{Z}\). Đáp án B Câu 7: Tìm tất cả các tham số thực m để phương trình \({\sin ^2}x + \sin x\cos x = m\) có nghiệm.
Phương pháp Sử dụng kiến thức: Phương trình \(a\sin x + b\cos x = c\) có nghiệm khi \({c^2} \le {a^2} + {b^2}\) Lời giải \({\sin ^2}x + \sin x\cos x = m \Leftrightarrow \frac{{1 - \cos 2x}}{2} + \frac{1}{2}\sin 2x = m \Leftrightarrow 1 - \cos 2x + \sin 2x = 2m\) \( \Leftrightarrow - \cos 2x + \sin 2x = 2m - 1\) (1) Phương trình (1) có nghiệm khi và chỉ khi \({\left( { - 1} \right)^2} + {1^2} \ge {\left( {2m - 1} \right)^2} \Leftrightarrow {\left( {2m - 1} \right)^2} \le 2 \Leftrightarrow - \sqrt 2 \le 2m - 1 \le \sqrt 2 \Leftrightarrow \frac{{1 - \sqrt 2 }}{2} \le m \le \frac{{1 + \sqrt 2 }}{2}\) Đáp án B Câu 8: Dãy số có các số hạng đầu là \(0;\frac{1}{2};\frac{2}{3};\frac{3}{4};\frac{4}{5};...\) Số hạng tổng quát của dãy số này là:
Phương pháp Tìm công thức số hạng tổng quát của dãy số \(\left( {{u_n}} \right)\): Từ các số đã cho của dãy số, biến đổi sao cho các số hạng có chung một quy luật theo n, từ đó tìm được công thức số hạng tổng quát \({u_n}\). Lời giải Ta có: \({u_1} = 0 = \frac{{1 - 1}}{1};{u_2} = \frac{1}{2} = \frac{{2 - 1}}{2};{u_3} = \frac{2}{3} = \frac{{3 - 1}}{3};{u_4} = \frac{3}{4} = \frac{{4 - 1}}{4};{u_5} = \frac{4}{5} = \frac{{5 - 1}}{5};...\) Dự đoán công thức số hạng tổng quát: \({u_n} = \frac{{n - 1}}{n}\). Đáp án C Câu 9: Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + ... + \frac{1}{{{n^2}}},\forall n = 2;{\rm{ }}3;{\rm{ }}4; \cdots .\) Mệnh đề nào sau đây đúng?
Phương pháp Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số bị chặn trên nếu tồn tại một số M sao cho \({u_n} \le M\;\forall n \in \mathbb{N}*\). Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số bị chặn dưới nếu tồn tại một số m sao cho \({u_n} \ge m\;\forall n \in \mathbb{N}*\). Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, nghĩa là tồn tại các số M và m sao cho \(m \le {u_n} \le M\;\forall n \in \mathbb{N}*\). Lời giải Ta có \({u_n} > 0\;\forall n = 2;{\rm{ }}3;{\rm{ }}4; \cdots \) nên \({u_n}\) bị chặn dưới bởi 0. Mặt khác \(\frac{1}{{{k^2}}} < \frac{1}{{\left( {k - 1} \right)k}}\,\, = \frac{1}{{k - 1}} - \frac{1}{k}\,\,\left( {k \in {\mathbb{N}^*},\,k \ge 2} \right)\) nên suy ra: \({u_n} < \frac{1}{{1.2}} + \frac{1}{{2.3}} + \frac{1}{{3.4}} + \cdots + \frac{1}{{n\left( {n + 1} \right)}} = 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \frac{1}{2} - \frac{1}{4} + \cdots + \frac{1}{n} - \frac{1}{{n + 1}} = 1 - \frac{1}{{n + 1}} < 1\) Do đó, dãy \(\left( {{u_n}} \right)\) bị chặn trên. Vậy dãy số \(\left( {{u_n}} \right)\) bị chặn. Đáp án C Câu 10: Trong các dãy số được cho dưới đây, dãy số nào là cấp số cộng?
Phương pháp Cấp số cộng là một dãy số, trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng tổng của số hạng đứng ngay trước nó với một số không đổi d, tức là: \({u_n} = {u_{n - 1}} + d\) với \(n \ge 2\). Lời giải Xét dãy số: \({u_n} = 8 - 3n\), ta có: \({u_1} = 5;{u_2} = 2;{u_3} = - 1;{u_4} = - 4;..\) Nhận thấy các số hạng, kể từ số hạng thứ hai trở đi, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với \( - 3\) nên dãy số \({u_n} = 8 - 3n\) là cấp số cộng Đáp án D Câu 11: Một công ty thực hiện việc trả lương cho các kỹ sư theo phương thức sau: Mức lương của quý làm việc đầu tiên cho công ty là 14 triệu đồng/ quý và kể từ quý làm việc thứ hai, mức lương sẽ được tăng 500 000 đồng mỗi quý. Tổng số tiền một kỹ sư nhận được sau ba năm làm việc tại công ty là:
Phương pháp Cho cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công sai d. Đặt \({S_n} = {u_1} + {u_2} + {u_3} + ... + {u_n}\). Khi đó: \({S_n} = \frac{{\left( {{u_1} + {u_n}} \right)n}}{2} = \frac{{\left[ {2{u_1} + \left( {n - 1} \right)d} \right]n}}{2}\) Lời giải Gọi \({u_n}\) là mức lương của quý thứ n làm việc tại công ty. Khi đó, dãy số \(\left( {{u_n}} \right)\) lập thành một cấp số cộng có số hạng đầu \({u_1} = 14\) và công sai \(d = 0,5\) Một năm có 4 quý nên 3 năm có 12 quý. Do đó, để tính số tiền kỹ sư nhận được sau ba năm, ta đi tính tổng 12 số hạng đầu tiên của cấp số cộng. Số tiền người kĩ sư nhận được là: \({S_{12}} = \frac{{12\left[ {2.14 + \left( {12 - 1} \right).0,5} \right]}}{2} = 201\) (triệu đồng) Đáp án B Câu 12: Cho ba góc của một tam giác lập thành một cấp số cộng, trong đó góc lớn nhất gấp đôi góc nhỏ nhất. Số đo góc lớn nhất của tam giác là:
Phương pháp Cho cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công sai d thì số hạng tổng quát được xác định theo công thức \({u_n} = {u_1} + \left( {n - 1} \right)d\) Lời giải Không làm mất tính tổng quát, gọi ba góc A, B, C của tam giác ABC theo thứ tự từ bé đến lớn lập thành một cấp số cộng có công sai là d. Khi đó, \(\widehat B = \widehat A + d,\widehat C = \widehat B + d = \widehat A + 2d \Rightarrow \widehat A + \widehat C = 2\widehat B\) Theo giả thiết ta có: \(\widehat A + \widehat B + \widehat C = {180^0},\widehat C = 2\widehat A\) Do đó, ta có hệ phương trình: \(\left\{ \begin{array}{l}\widehat A + \widehat C = 2\widehat B\\\widehat A + \widehat B + \widehat C = {180^0}\\\widehat C = 2\widehat A\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\widehat A = {40^0}\\\widehat B = {60^0}\\\widehat C = {80^0}\end{array} \right.\) Vậy góc có số đo lớn nhất là \({80^0}\) Đáp án D Câu 13: Dãy số gồm các số tự nhiên lẻ nhỏ hơn 20, sắp xếp theo thứ tự từ bé đến lớn là:
Phương pháp Hàm số u xác định trên tập hợp \(M = \left\{ {1;2;3;..;m} \right\}\) thì được gọi là một dãy số hữu hạn. Dạng triển khai của dãy số này là \({u_1},{u_2},...,{u_m}\). Lời giải Dãy số gồm các số tự nhiên lẻ nhỏ hơn 20, sắp xếp theo thứ tự từ bé đến lớn là dãy số hữu hạn: \(1;3;5;7;9;11;13;15;17;19\) Đáp án A Câu 14: Hình nào trong các hình sau đây là hình chóp tứ giác?
Phương pháp Cho đa giác lồi \({A_1}{A_2}{A_3}....{A_n}\) nằm trong mặt phẳng \(\left( \alpha \right)\) và điểm S không thuộc \(\left( \alpha \right)\). Nối S với các đỉnh \({A_1};{A_2};{A_3};...;{A_n}\) ta được n tam giác \(S{A_1}{A_2};S{A_2}{A_3};...;S{A_n}{A_1}\). Hình được tạo bởi n tam giác đó và đa giác \({A_1}{A_2}{A_3}....{A_n}\) được gọi là hình chóp, kí hiệu là \(S.{A_1}{A_2}{A_3}....{A_n}\). Lời giải Hình 2 là hình chóp tứ giác. Đáp án B Câu 15: Cho tam giác ABC và điểm S không nằm trong mặt phẳng chứa tam giác ABC. Có bao nhiêu mặt phẳng được tạo thành?
Phương pháp Một mặt phẳng được xác định nếu biết nó chứa ba điểm không thẳng hàng. Lời giải Các mặt phẳng được tạo thành là: (SAB), (SAC), (SBC), (ABC). Vậy có 4 mặt phẳng được tạo thành. Đáp án D Câu 16: Cho hình chóp S. ABCD có đáy ABCD là hình thang với AB là đáy lớn. Trên đoạn SA, lấy điểm I không trùng với S và A; trên đoạn BC lấy điểm J không trùng với B và C. Giao tuyến của đường thẳng IJ và mặt phẳng (SBD) là:
Phương pháp Cách tìm giao điểm của đường thẳng d và mặt phẳng \(\left( \alpha \right)\): Trường hợp 1: \(\left( \alpha \right)\) chứa đường thẳng d’ và d’ cắt đường thẳng d tại I. Khi đó, \(I = d \cap d' \Rightarrow I = d \cap \left( \alpha \right)\) Trường hợp 2: \(\left( \alpha \right)\) không chứa đường thẳng nào cắt d. + Tìm mặt phẳng \(\left( \beta \right)\) chứa d và \(\left( \alpha \right) \cap \left( \beta \right) = d'\) + Tìm \(I = d \cap d'\). Khi đó, \(I = d \cap \left( \alpha \right)\) Lời giải Trong mặt phẳng (ABCD), gọi K là giao điểm của AJ và BD nên K thuộc mặt phẳng (SBD) và mặt phẳng (SAJ). Lại có, S thuộc mặt phẳng (SBD) và mặt phẳng (SAJ). Do đó, \(SK = mp\left( {SAJ} \right) \cap mp\left( {SBD} \right)\) Trong mặt phẳng (SAJ), gọi H là giao điểm của SK và IJ. Vì \(H \in IJ,H \in SK \subset mp\left( {SBD} \right)\) Vậy H là giao điểm của SK và mặt phẳng (SBD). Đáp án A Câu 17: Cho hình chóp tam giác S. ABC. Trong các cặp đường thẳng sau, cặp đường thẳng nào không chéo nhau?
Phương pháp Nếu không có mặt phẳng nào chứa hai đường thẳng a và b thì khi đó ta nói đường thẳng a và b chéo nhau. Lời giải Hai đường thẳng SB và SC cùng nằm trong mặt phẳng (SBC) nên hai đường thẳng này không chéo nhau. Đáp án C Câu 18: Cho tứ diện ABCD. Gọi I, J lần lượt là trọng tâm của các tam giác ABC và ABD. Gọi M, N lần lượt là trung điểm của BC và BD. Trong các đường thẳng MN, CD, BD, BC thì IJ song song với bao nhiêu đường thẳng?
Phương pháp Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau. Lời giải Vì M, N lần lượt là trung điểm của BC và BD nên MN là đường trung bình của tam giác BCD. Do đó, MN//CD Vì I là trọng tâm tam giác ABC nên \(\frac{{AI}}{{AM}} = \frac{2}{3}\) Vì J là trọng tâm tam giác ABD nên \(\frac{{AJ}}{{AN}} = \frac{2}{3}\) Do đó, \(\frac{{AJ}}{{AN}} = \frac{{AI}}{{AM}}\) nên IJ//MN (định lí Thalès đảo) Vì IJ//MN, MN//CD nên IJ//CD Vậy đường thẳng IJ song song với hai đường thẳng là MN và CD. Đáp án B Câu 19: Cho hình chóp tứ giác S. ABCD có M, N, I, K lần lượt là trung điểm của SA, SC, AD, CD. Tứ giác MNKI là hình gì?
Phương pháp Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau. Lời giải Vì M, N lần lượt là trung điểm của SA, SC nên MN là đường trung bình của tam giác SAC. Do đó, MN//AC, \(MN = \frac{1}{2}AC\) Vì I, K lần lượt là trung điểm của DA, DC nên IK là đường trung bình của tam giác DAC. Do đó, IK//AC, \(IK = \frac{1}{2}AC\) Do đó, IK//MN, \(IK = MN\). Vậy tứ giác MNKI là hình bình hành. Đáp án D Câu 20: Cho các số a, b, c \(\left( {a < b < c,c \in \mathbb{Z}} \right)\) lập thành cấp số nhân; đồng thời \(a,b + 8,c\) theo thứ tự lập thành cấp số cộng và \(a,b + 8,c + 64\) theo thứ tự lập thành cấp số nhân. Giá trị biểu thức \(P = a + b + c\) là:
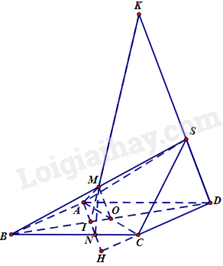
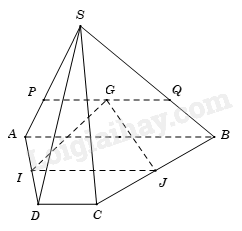
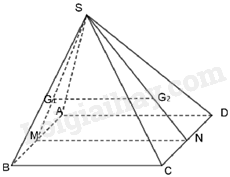
Phương pháp Cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu là \({u_1}\) và công bội q thì số hạng tổng quát \({u_n}\) của nó được xác định bởi công thức \({u_n} = {u_1}.{q^{n - 1}}\) với \(n \ge 2\). Lời giải Theo đầu bài ta có hệ phương trình: \(\left\{ \begin{array}{l}ac = {b^2}\\a + c = 2\left( {b + 8} \right)\\a\left( {c + 64} \right) = {\left( {b + 8} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}ac = {b^2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\a - 2b = 16 - c\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\\ac + 64a = {\left( {b + 8} \right)^2}\,\,\,\,\,\left( 3 \right)\end{array} \right..\) Thay (1) vào (3) ta có: \({b^2} + 64a = {b^2} + 16b + 64 \Leftrightarrow 4a - b = 4\,\,\left( 4 \right).\) Kết hợp (2) và (4) ta có: \(\left\{ \begin{array}{l}a - 2b = 16 - c\\4a - b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{{c - 8}}{7}\\b = \frac{{4c - 60}}{7}\end{array} \right.\,\,\,\,\,\left( 5 \right)\)\(\) Thay (5) vào (1) ta có: \(7\left( {c - 8} \right)c = {\left( {4c - 60} \right)^2} \Leftrightarrow 9{c^2} - 424c + 3600 = 0 \Leftrightarrow \left[ \begin{array}{l}c = 36\\c = \frac{{100}}{9}\end{array} \right. \Leftrightarrow c = 36\,\,\left( {c \in \mathbb{Z}} \right).\) Với \(c = 36 \Rightarrow a = 4,b = 12 \Rightarrow P = 36 + 4 + 12 = 52\) Đáp án A Phần tự luận (5 điểm) Bài 1. (1,5 điểm) 1) Giải các phương trình sau: a) \({\sin ^2}x - {\cos ^2}x + \cos 3x = 0\) b) \(\sin x + \sqrt 3 \cos x = 0\) 2) Tìm giá trị nhỏ nhất, lớn nhất của hàm số \(y = 2{\sin ^2}x + \sqrt 3 \sin 2x\) 3) Phương trình \({\tan ^4}x + 1 = \frac{{\left( {2 - {{\sin }^2}2x} \right)\sin 3x}}{{{{\cos }^4}x}}\) có bao nhiêu nghiệm thuộc \(\left( {\frac{\pi }{2};\pi } \right)\)? Phương pháp 1) a) + Xét phương trình \(\cos x = m\) * Nếu \(\left| m \right| > 1\) thì phương trình vô nghiệm. * Nếu \(\left| m \right| \le 1\) thì phương trình có nghiệm: \(x = \alpha + k2\pi ,k \in \mathbb{Z}\) và \(x = - \alpha + k2\pi ,k \in \mathbb{Z}\), với \(\alpha \) là góc thuộc \(\left[ {0;\pi } \right]\) sao cho \(\cos \alpha = m\) b) \(\sin \alpha = 0 \Leftrightarrow \alpha = k\pi \left( {k \in \mathbb{Z}} \right)\) 2) Sử dụng kiến thức \( - 1 \le \sin x \le 1\) 3) + tanx xác định khi \(\cos x \ne 0\) + Xét phương trình \(\sin x = m\) * Nếu \(\left| m \right| > 1\) thì phương trình vô nghiệm. * Nếu \(\left| m \right| \le 1\) thì phương trình có nghiệm: \(x = \alpha + k2\pi ,k \in \mathbb{Z}\) và \(x = \pi - \alpha + k2\pi ,k \in \mathbb{Z}\), với \(\alpha \) là góc thuộc \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) sao cho \(\sin \alpha = m\) Lời giải 1) a) \({\sin ^2}x - {\cos ^2}x + \cos 3x = 0 \Leftrightarrow \cos 3x - \cos 2x = 0 \Leftrightarrow \cos 3x = \cos 2x\) \( \Leftrightarrow \left[ \begin{array}{l}3x = 2x + k2\pi \\3x = - 2x + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right) \Leftrightarrow \left[ \begin{array}{l}x = k2\pi \\x = \frac{{k2\pi }}{5}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\) Vậy phương trình đã cho có họ nghiệm là \(x = k2\pi ,x = \frac{{k2\pi }}{5}\left( {k \in \mathbb{Z}} \right)\) b) \(\sin x + \sqrt 3 \cos x = 0 \Leftrightarrow \frac{1}{2}\sin x + \frac{{\sqrt 3 }}{2}\cos x = 0 \Leftrightarrow \cos \frac{\pi }{3}\sin x + \sin \frac{\pi }{3}\cos x = 0\) \( \Leftrightarrow \sin \left( {x + \frac{\pi }{3}} \right) = 0 \Leftrightarrow x + \frac{\pi }{3} = k\pi \left( {k \in \mathbb{Z}} \right) \Leftrightarrow x = - \frac{\pi }{3} + k\pi \left( {k \in \mathbb{Z}} \right)\) Vậy phương trình đã cho có họ nghiệm là \(x = - \frac{\pi }{3} + k\pi \left( {k \in \mathbb{Z}} \right)\) 2) Ta có: \(y = 2{\sin ^2}x + \sqrt 3 \sin 2x = 1 - \cos 2x + \sqrt 3 \sin 2x\) \( = \sqrt 3 \sin 2x - \cos 2x + 1 = 2\left( {\frac{{\sqrt 3 }}{2}\sin 2x - \frac{1}{2}\cos 2x} \right) + 1\) \( = 2\left( {\sin 2x\cos \frac{\pi }{6} - \sin \frac{\pi }{6}\cos 2x} \right) + 1 = 2\sin \left( {2x - \frac{\pi }{6}} \right) + 1.\) Mà \( - 1 \le \sin \left( {2x - \frac{\pi }{6}} \right) \le 1 \Rightarrow - 1 \le 1 + 2\sin \left( {2x - \frac{\pi }{6}} \right) \le 3 \Rightarrow - 1 \le y \le 3.\) Do đó, giá trị nhỏ nhất của hàm số là \( - 1\), giá trị lớn nhất của hàm số là 3. 3) Điều kiện: \(\cos x \ne 0\) \({\tan ^4}x + 1 = \frac{{\left( {2 - {{\sin }^2}2x} \right)\sin 3x}}{{{{\cos }^4}x}} \Leftrightarrow {\sin ^4}x + {\cos ^4}x = \left( {2 - {{\sin }^2}2x} \right)\sin 3x\) \( \Leftrightarrow {\left( {{{\sin }^2}x + {{\cos }^2}x} \right)^2} - 2{\sin ^2}x{\cos ^2}x = \left( {2 - {{\sin }^2}2x} \right)\sin 3x\) \( \Leftrightarrow 1 - \frac{1}{2}{\sin ^2}2x = \left( {2 - {{\sin }^2}2x} \right)\sin 3x \Leftrightarrow 2 - {\sin ^2}2x = 2\left( {2 - {{\sin }^2}2x} \right)\sin 3x\) \( \Leftrightarrow \left( {2 - {{\sin }^2}2x} \right)\left( {1 - 2\sin 3x} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}2 - {\sin ^2}2x = 0\\1 - 2\sin 3x = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\sin 2x = \pm \sqrt 2 \left( {VL} \right)\\\sin 3x = \frac{1}{2}\end{array} \right.\) \( \Leftrightarrow \sin 3x = \sin \frac{\pi }{6} \Leftrightarrow \left[ \begin{array}{l}3x = \frac{\pi }{6} + k2\pi \\3x = \pi - \frac{\pi }{6} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right) \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{{18}} + \frac{{k2\pi }}{3}\\x = \frac{{5\pi }}{{18}} + \frac{{k2\pi }}{3}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\) (thỏa mãn điều kiện) Lại có: \(x \in \left( {\frac{\pi }{2};\pi } \right)\) nên \(\left[ \begin{array}{l}\frac{\pi }{2} < \frac{\pi }{{18}} + \frac{{k2\pi }}{3} < \pi \\\frac{\pi }{2} < \frac{{5\pi }}{{18}} + \frac{{k2\pi }}{3} < \pi \end{array} \right.\left( {k \in \mathbb{Z}} \right) \Leftrightarrow \left[ \begin{array}{l}\frac{2}{3} < k < \frac{{17}}{{12}}\\\frac{1}{3} < k < \frac{{13}}{{12}}\end{array} \right.\left( {k \in \mathbb{Z}} \right) \Leftrightarrow \left[ \begin{array}{l}k = 1\\k = 1\end{array} \right.\) Với \(k = 1\) thì \(x = \frac{{13\pi }}{{18}}\) hoặc \(x = \frac{{17\pi }}{{18}}\) (thỏa mãn điều kiện). Vậy có hai nghiệm thuộc \(\left( {\frac{\pi }{2};\pi } \right)\) Bài 2. (1,5 điểm) a) Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = 4,{u_2} = 10.\) Tính \({u_{100}}\). b) Cho dãy số \(\left( {{u_n}} \right)\): \(\left( {{u_n}} \right):\left\{ \begin{array}{l}{u_1} = 3\\{u_{n + 1}} = \sqrt {1 + u_n^2} \end{array} \right.\). Tìm công thức số hạng tổng quát của dãy số trên. Phương pháp a) Nếu một cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công sai d thì số hạng tổng quát \({u_n}\) của nó được xác định bởi công thức: \({u_n} = {u_1} + \left( {n - 1} \right)d,n \ge 2\) b) Công thức truy hồi là hệ thức biểu thị số hạng thứ n của dãy số qua số hạng (hay vài số hạng) đứng trước nó. Lời giải a) Ta có: \(d = {u_2} - {u_1} = 10 - 4 = 6\). Do đó, \({u_{100}} = {u_1} + \left( {100 - 1} \right)d = 4 + 99.6 = 598\) b) Ta có \(\begin{array}{l}{u_1} = 3 = \sqrt {{3^2} + 0} \\{u_2} = \sqrt {10} = \sqrt {{3^2} + 1} \\{u_3} = \sqrt {11} = \sqrt {{3^2} + 2} \\{u_4} = \sqrt {12} = \sqrt {{3^2} + 3} \\...\\{u_n} = \sqrt {{3^2} + n - 1} \,\,\left( * \right)\end{array}\) Vậy công thức số hạng tổng quát của dãy số là: \({u_n} = \sqrt {{3^2} + n - 1} \) Bài 3. (1,0 điểm) Cho hình chóp S. ABCD có đáy là hình bình hành tâm O. Gọi M là trung điểm của SB. N là điểm trên cạnh BC sao cho \(BN = 2CN\). Xác định giao tuyến của mặt phẳng (SCD) và mặt phẳng (AMN). Phương pháp Nếu hai mặt phân biệt (P) và (Q) có điểm chung thì chúng có một đường thẳng chung duy nhất d chứa tất cả các điểm chung của hai mặt phẳng đó. Đường thẳng d đó gọi là giao tuyến của hai mặt phẳng (P) và (Q), kí hiệu \(d = \left( P \right) \cap \left( Q \right)\) Lời giải Trong mặt phẳng (ABCD), gọi H là giao điểm của AN và CD Vì H thuộc AN nên H thuộc mặt phẳng (AMN), H thuộc DC nên H thuộc mặt phẳng (SCD). Trong mặt phẳng (ABCD), gọi I là giao điểm của AN và BD nên I thuộc mặt phẳng (SBD). Trong mặt phẳng (SBD), gọi K là giao điểm của IM và SD nên K thuộc mặt phẳng (AMN) và mặt phẳng (SCD). Do đó, HK là giao tuyến của hai mặt phẳng (AMN) và mặt phẳng (SCD). Bài 4. (1,0 điểm) a) Cho hình chóp S. ABCD có đáy là hình thang với đáy lớn là AB. Gọi I, J lần lượt là trung điểm của AD và BC và G là trọng tâm của tam giác SAB. Tìm giao tuyến của mặt phẳng (SAB) và mặt phẳng (IJG) b) Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi \({G_1},{G_2}\) lần lượt là trọng tâm các tam giác SAB và SCD. Gọi M, N lần lượt là trung điểm của AB, CD. Chứng minh rằng \({G_1}{G_2}\)//AD//BC Phương pháp Nếu hai mặt phẳng phân biệt lần lượt đi qua hai đường thẳng song song thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó. Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau. Lời giải
|