Đề thi giữa kì 1 Toán 11 Cánh diều - Đề số 7Tổng hợp đề thi học kì 2 lớp 11 tất cả các môn - Cánh diều Toán - Văn - Anh - Lí - Hóa - Sinh Phần trắc nghiệmĐề bài
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 :
Góc có số đo \(\frac{\pi }{6}\) radian bằng bao nhiêu độ?
Câu 2 :
Cho \(\cos \alpha = - \frac{1}{4}\) với \(\pi < \alpha < \frac{{3\pi }}{2}\). Giá trị của \(\sin \alpha \) là?
Câu 3 :
Giá trị lượng giác \(\cos \left( {\frac{{37\pi }}{{12}}} \right)\) bằng?
Câu 4 :
Hàm số nào sau đây là hàm số chẵn?
Câu 5 :
Nghiệm của phương trình \(\cos x = 0\) là?
Câu 6 :
Số hạng thứ 3 của dãy số \(\left\{ {\begin{array}{*{20}{c}}{{u_1} = 1}\\{{u_n} = 2{u_{n - 1}} + 3}\end{array}} \right.\) là?
Câu 7 :
Dãy số nào sau đây là cấp số cộng?
Câu 8 :
Cho dãy số có các số hạng đầu là \(0;\frac{1}{2};\frac{2}{3};\frac{3}{4};\frac{4}{5};...\) Số hạng tổng quát của dãy số là:
Câu 9 :
Các yếu tố nào sau đây xác định một mặt phẳng?
Câu 11 :
Số nghiệm của phương trình \(\sin 2x + \cos x = 0\) trên \([0;2\pi ]\) là
Câu 12 :
Cho cấp số cộng \(({u_n})\) có \({u_5} = - 10\) và \({u_{15}} = 60\). Tổng 20 số hạng đầu tiên của cấp số cộng là
Phần II: Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1 :
Cho phương trình lượng giác \(2\sin \left( {x - \frac{\pi }{{12}}} \right) + \sqrt 3 = 0\). Khi đó a) Phương trình tương đương \(\sin \left( {x - \frac{\pi }{{12}}} \right) = \sin \frac{\pi }{3}\)
Đúng
Sai
b) Phương trình có nghiệm là \(x = \frac{\pi }{4} + k2\pi \); \(x = \frac{{7\pi }}{{12}} + k2\pi \) \((k \in \mathbb{Z})\)
Đúng
Sai
c) Phương trình có nghiệm âm lớn nhất bằng \( - \frac{\pi }{4}\)
Đúng
Sai
d) Số nghiệm của phương trình trong khoảng \(( - \pi ;\pi )\) là hai nghiệm
Đúng
Sai
Câu 2 :
Cho \(\cos \alpha = - \frac{1}{4}\) và \(\pi < \alpha < \frac{{3\pi }}{2}\). Khi đó a) \({\sin ^2}\alpha = \frac{{15}}{{16}}\)
Đúng
Sai
b) \(\sin \alpha = \frac{{\sqrt {15} }}{4}\)
Đúng
Sai
c) \(\tan \alpha = \sqrt {15} \)
Đúng
Sai
d) \(\cot \alpha = - \frac{1}{{\sqrt {15} }}\)
Đúng
Sai
Câu 3 :
Cho dãy số \(({u_n})\) biết \({u_n} = {2^n} + 1\). Khi đó a) Dãy số \(({u_n})\) là dãy số tăng
Đúng
Sai
b) Dãy số \(({u_n})\) là dãy số bị chặn
Đúng
Sai
c) \({u_6} = 65\)
Đúng
Sai
d) Số hạng thứ n + 2 của dãy số là \({u_{n + 2}} = {2^n}.2\)
Đúng
Sai
Câu 4 :
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Mặt phẳng (P) qua BD và song song với SA. Khi đó a) Giao tuyến của hai mặt phẳng (SAB) và (SAD) là SO
Đúng
Sai
b) SO thuộc mặt phẳng (SBD)
Đúng
Sai
c) Gọi I là giao điểm của SC và (P). Khi đó OI//SA
Đúng
Sai
d) Thiết diện giữa (P) và hình chóp là hình bình hành
Đúng
Sai
Phần III: Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1 :
Hằng ngày mực nước tại một cảng biển lên xuống theo thủy triều. Độ sâu h (m) của mực nước theo thời gian t (giờ) trong một ngày được cho bởi công thức \(h = 11 + 2\sin \left( {\frac{\pi }{{12}}t} \right)\) với \(0 \le t \le 24\). Tính thời điểm mực nước tại cảng cao nhất. Đáp án:
Câu 2 :
Phương trình \(2\sin 2x + 4\cos x = 0\) có bao nhiêu nghiệm trong khoảng (0;3000)? Đáp án:
Câu 3 :
Công ty cây xanh X trồng 496 cây hoa trong một khu vườn hình tam giác như sau: hàng thứ nhất trồng 1 cây hoa, kể từ hàng thứ hai trở đi số cây hoa trồng mỗi hàng nhiều hơn 1 cây so với hàng liền trước nó. Hỏi công ty cây xanh X trồng được bao nhiêu hàng cây trong khu vườn hình tam giác đó. Đáp án:
Câu 4 :
Cho dãy số \(({u_n})\) biết \({u_n} = n + \frac{1}{n}\). Tìm m để dãy số \(({u_n})\) bị chặn dưới bởi m. Đáp án:
Câu 5 :
Cho tứ diện ABCD. Điểm I và J theo thức tự là trung điểm của AD và AC, G là trọng tâm tam giác BCD. Giao tuyến của hai mặt phẳng (GIJ) và (BCD) cắt BD tại E, cắt BC tại F. Tính tỉ số \(\frac{{IJ}}{{EF}}\) (Viết dưới dạng số thập phân)? Đáp án:
Câu 6 :
Cho hình chóp S.ABCD có đáy hình bình hành. Trên cạnh SA lấy điểm M sao cho MA = 2MS. Mặt phẳng (CDM) cắt SB tại N. Biết rằng AB = 3 cm, tính tổng MN + CD.
Đáp án: Lời giải và đáp án
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 :
Góc có số đo \(\frac{\pi }{6}\) radian bằng bao nhiêu độ?
Đáp án : A Phương pháp giải :
Áp dụng quan hệ giữa radian và độ: \(1rad = {\left( {\frac{{180}}{\pi }} \right)^o}\), \({1^o} = \frac{\pi }{{180}}rad\). Lời giải chi tiết :
Ta có: \(\frac{\pi }{6}rad = \frac{\pi }{6}.\frac{{{{180}^o}}}{\pi } = {30^o}\).
Câu 2 :
Cho \(\cos \alpha = - \frac{1}{4}\) với \(\pi < \alpha < \frac{{3\pi }}{2}\). Giá trị của \(\sin \alpha \) là?
Đáp án : B Phương pháp giải :
Áp dụng công thức \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) và sử dụng đường tròn lượng giác để xét dấu. Lời giải chi tiết :
Ta có: \({\sin ^2}\alpha = 1 - {\cos ^2}\alpha = 1 - {\left( {\frac{1}{4}} \right)^2} = \frac{{15}}{{16}}\), suy ra \(\sin \alpha = \pm \frac{{\sqrt {15} }}{4}\). Vì \(\pi < \alpha < \frac{{3\pi }}{2}\) nên điểm cuối của cung \(\alpha \) thuộc cung phần tư thứ III, do đó \(\sin \alpha < 0\). Vậy \(\sin \alpha = - \frac{{\sqrt {15} }}{4}\).
Câu 3 :
Giá trị lượng giác \(\cos \left( {\frac{{37\pi }}{{12}}} \right)\) bằng?
Đáp án : C Phương pháp giải :
Sử dụng công thức cộng lượng giác \(\cos (a - b) = \cos a.\cos b + \sin b.\sin a\). Lời giải chi tiết :
\(\cos \frac{{37\pi }}{{12}} = \cos \left( {3\pi + \frac{\pi }{{12}}} \right) = \cos \left( {\pi + \frac{\pi }{{12}}} \right) = - \cos \frac{\pi }{{12}} = - \cos \left( {\frac{\pi }{3} - \frac{\pi }{4}} \right)\) \( = - \left( {\cos \frac{\pi }{3}.\cos \frac{\pi }{4} + \sin \frac{\pi }{3}.\sin \frac{\pi }{4}} \right) = - \frac{{\sqrt 6 + \sqrt 2 }}{4}\).
Câu 4 :
Hàm số nào sau đây là hàm số chẵn?
Đáp án : A Phương pháp giải :
Cho hàm số y = f(x) liên tục và xác định trên khoảng (đoạn) K. Với mỗi \(x \in K\) thì \( - x \in K\). - Nếu f(x) = f(-x) thì hàm số y = f(x) là hàm số chẵn trên tập xác định. - Nếu f(-x) = -f(x) thì hàm số y = f(x) là hàm số lẻ trên tập xác định. Lời giải chi tiết :
Xét phương án A, hàm số \(y = \left| {\sin x} \right|\) có tập xác định D = R, suy ra có \(x \in R\) thì \( - x \in R\). Mặt khác, \(f( - x) = \left| {\sin ( - x)} \right| = \left| { - \sin x} \right| = \sin x = f(x)\). Vậy hàm số đáp án A là hàm số chẵn.
Câu 5 :
Nghiệm của phương trình \(\cos x = 0\) là?
Đáp án : C Phương pháp giải :
Nghiệm của phương trình lượng giác cơ bản. Lời giải chi tiết :
\(\cos x = 0 \Leftrightarrow x = \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\).
Câu 6 :
Số hạng thứ 3 của dãy số \(\left\{ {\begin{array}{*{20}{c}}{{u_1} = 1}\\{{u_n} = 2{u_{n - 1}} + 3}\end{array}} \right.\) là?
Đáp án : D Phương pháp giải :
Tìm lần lượt \({u_2},{u_3}\) bằng cách thay n vào công thức tổng quát. Lời giải chi tiết :
Ta có: \({u_2} = 2{u_{2 - 1}} + 3 = 2{u_1} + 3 = 2.1 + 3 = 5\) \({u_3} = 2{u_{3 - 1}} + 3 = 2{u_2} + 3 = 2.5 + 3 = 13\)
Câu 7 :
Dãy số nào sau đây là cấp số cộng?
Đáp án : C Phương pháp giải :
Dãy số lập thành một cấp số cộng khi và chỉ khi hai phần tử liên tiếp sai khác nhau một hằng số. Lời giải chi tiết :
Xét hiệu các phần tử liên tiếp trong các dãy số, chỉ có dãy ở đáp án C phần tử sau hơn phần tử liền trước 2 đơn vị (8 – 6 = 6 – 4 = 4 – 2 = 2 – 0 = 2).
Câu 8 :
Cho dãy số có các số hạng đầu là \(0;\frac{1}{2};\frac{2}{3};\frac{3}{4};\frac{4}{5};...\) Số hạng tổng quát của dãy số là:
Đáp án : B Phương pháp giải :
Viết các số hạng đầu của từng đáp án để kiểm tra. Lời giải chi tiết :
Ta có: \(0 = \frac{0}{{0 + 1}}\); \(\frac{1}{2} = \frac{1}{{1 + 1}}\); \(\frac{2}{3} = \frac{1}{{2 + 1}}\); \(\frac{3}{4} = \frac{3}{{3 + 1}}\); \(\frac{4}{5} = \frac{4}{{4 + 1}}\). Vậy \({u_n} = \frac{n}{{n + 1}}\).
Câu 9 :
Các yếu tố nào sau đây xác định một mặt phẳng?
Đáp án : C Phương pháp giải :
Dựa vào lý thuyết các xác định một mặt phẳng. Lời giải chi tiết :
Một mặt phẳng được xác định nếu nó đi qua: - Ba điểm không thẳng hàng - Một điểm và một đường thẳng không đi qua điểm đó. - Hai đường thẳng cắt nhau.
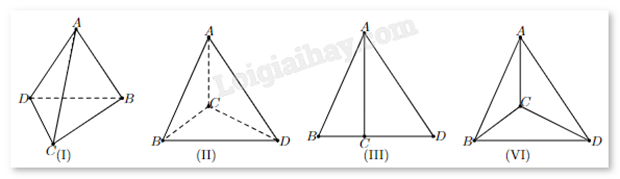
Đáp án : D Phương pháp giải :
Tứ diện là hình có 4 mặt và 4 đỉnh. Lời giải chi tiết :
Cả 4 hình đều là tứ diện (4 mặt và 4 đỉnh). Hình (I) và (III) có thể nhìn thấy 2 mặt. Hình (II) có thể nhìn thấy 1 mặt. Hình (IV) có thể nhìn thấy 3 mặt.
Câu 11 :
Số nghiệm của phương trình \(\sin 2x + \cos x = 0\) trên \([0;2\pi ]\) là
Đáp án : D Phương pháp giải :
Biến đổi phương trình trở thành dạng phương trình tích, đưa về giải phương trình lượng giác cơ bản. Lời giải chi tiết :
\(\sin 2x + \cos x = 0 \Leftrightarrow 2\sin x.\cos x + \cos x = 0 \Leftrightarrow \cos x.(2\sin x + 1) = 0\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\cos x = 0}\\{2\sin x + 1 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\cos x = 0}\\{\sin x = - \frac{1}{2}}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{2} + k\pi }\\{x = - \frac{\pi }{6} + k2\pi }\\{x = \frac{{7\pi }}{6} + k2\pi }\end{array}} \right.} \right.\) với \(k \in \mathbb{Z}\). Vì \(x \in [0;2\pi ]\) nên chỉ có 4 nghiệm thỏa mãn: \(x = \left\{ {\frac{\pi }{2};\frac{{3\pi }}{2};\frac{{7\pi }}{6};\frac{{11\pi }}{6}} \right\}\).
Câu 12 :
Cho cấp số cộng \(({u_n})\) có \({u_5} = - 10\) và \({u_{15}} = 60\). Tổng 20 số hạng đầu tiên của cấp số cộng là
Đáp án : C Phương pháp giải :
Tìm số hạng đầu và công sai dựa theo công thức \({u_n} = {u_1} + (n - 1)d\). Từ đó tìm tổng 20 số hạng đầu tiên \({S_n} = \frac{{({u_1} + {u_n})n}}{2}\). Lời giải chi tiết :
Ta có: \(\left\{ {\begin{array}{*{20}{c}}{{u_5} = {u_1} + 4d}\\{{u_{15}} = {u_1} + 14d}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ - 10 = {u_1} + 4d}\\{60 = {u_1} + 14d}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{u_1} = - 38}\\{d = 7}\end{array}} \right.\) Từ đó ta tính được \({u_{20}} = - 38 + (20 - 1)7 = 95\). Vậy tổng 20 số hạng đầu của cấp số cộng là \({S_{20}} = \frac{{({u_1} + {u_{20}}).20}}{2} = \frac{{( - 38 + 95).20}}{2} = 570\).
Phần II: Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1 :
Cho phương trình lượng giác \(2\sin \left( {x - \frac{\pi }{{12}}} \right) + \sqrt 3 = 0\). Khi đó a) Phương trình tương đương \(\sin \left( {x - \frac{\pi }{{12}}} \right) = \sin \frac{\pi }{3}\)
Đúng
Sai
b) Phương trình có nghiệm là \(x = \frac{\pi }{4} + k2\pi \); \(x = \frac{{7\pi }}{{12}} + k2\pi \) \((k \in \mathbb{Z})\)
Đúng
Sai
c) Phương trình có nghiệm âm lớn nhất bằng \( - \frac{\pi }{4}\)
Đúng
Sai
d) Số nghiệm của phương trình trong khoảng \(( - \pi ;\pi )\) là hai nghiệm
Đúng
Sai
Đáp án
a) Phương trình tương đương \(\sin \left( {x - \frac{\pi }{{12}}} \right) = \sin \frac{\pi }{3}\)
Đúng
Sai
b) Phương trình có nghiệm là \(x = \frac{\pi }{4} + k2\pi \); \(x = \frac{{7\pi }}{{12}} + k2\pi \) \((k \in \mathbb{Z})\)
Đúng
Sai
c) Phương trình có nghiệm âm lớn nhất bằng \( - \frac{\pi }{4}\)
Đúng
Sai
d) Số nghiệm của phương trình trong khoảng \(( - \pi ;\pi )\) là hai nghiệm
Đúng
Sai
Phương pháp giải :
Giải phương trình lượng giác \(\sin x = a\): - Nếu \(\left| a \right| > 1\) thì phương trình vô nghiệm. - Nếu \(\left| a \right| \le 1\) thì chọn cung \(\alpha \) sao cho \(\sin \alpha = a\). Khi đó phương trình trở thành: \(\sin x = \sin \alpha \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \alpha + k2\pi }\\{x = \pi - \alpha + k2\pi }\end{array}} \right.\) với \(k \in \mathbb{Z}\). Lời giải chi tiết :
\(2\sin \left( {x - \frac{\pi }{{12}}} \right) + \sqrt 3 = 0 \Leftrightarrow \sin \left( {x - \frac{\pi }{{12}}} \right) = - \frac{{\sqrt 3 }}{2} \Leftrightarrow \sin \left( {x - \frac{\pi }{{12}}} \right) = \sin \left( { - \frac{\pi }{3}} \right)\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x - \frac{\pi }{{12}} = - \frac{\pi }{3} + k2\pi }\\{x - \frac{\pi }{{12}} = \pi + \frac{\pi }{3} + k2\pi }\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - \frac{\pi }{4} + k2\pi }\\{x = \frac{{17\pi }}{{12}} + k2\pi }\end{array}} \right.\) a) Sai. \(2\sin \left( {x - \frac{\pi }{{12}}} \right) + \sqrt 3 = 0 \Leftrightarrow \sin \left( {x - \frac{\pi }{{12}}} \right) = - \frac{{\sqrt 3 }}{2} \Leftrightarrow \sin \left( {x - \frac{\pi }{{12}}} \right) = \sin \left( { - \frac{\pi }{3}} \right)\) b) Sai. Phương trình có nghiệm là \(x = - \frac{\pi }{4} + k2\pi \); \(x = \frac{{17\pi }}{{12}} + k2\pi \) \((k \in \mathbb{Z})\). c) Đúng. + Xét họ nghiệm \(x = - \frac{\pi }{4} + k2\pi \): Nghiệm âm lớn nhất là \(x = - \frac{\pi }{4}\) khi k = 0. + Xét họ nghiệm \(x = \frac{{17\pi }}{{12}} + k2\pi \): Nghiệm âm lớn nhất là \(x = - \frac{{7\pi }}{{12}}\) khi k = -1. Vì \( - \frac{\pi }{4} > - \frac{{7\pi }}{{12}}\) nên nghiệm âm lớn nhất là \(x = - \frac{\pi }{4}\). d) Đúng. + Xét họ nghiệm \(x = - \frac{\pi }{4} + k2\pi \): \( - \pi < x < \pi \Leftrightarrow - \pi < - \frac{\pi }{4} + k2\pi < \pi \) \( \Leftrightarrow - 1 < - \frac{1}{4} + 2k < 1 \Leftrightarrow - \frac{3}{4} < 2k < \frac{5}{4} \Leftrightarrow - \frac{3}{8} < k < \frac{5}{8}\). Vậy chỉ có k = 0 thỏa mãn. Khi đó \(x = - \frac{\pi }{4}\). + Xét họ nghiệm \(x = \frac{{17\pi }}{{12}} + k2\pi \): \( - \pi < x < \pi \Leftrightarrow - \pi < \frac{{17\pi }}{{12}} + k2\pi < \pi \Leftrightarrow - 1 < \frac{{17}}{{12}} + 2k < 1\) \( \Leftrightarrow - \frac{{29}}{{12}} < 2k < - \frac{5}{{12}} \Leftrightarrow - \frac{{29}}{{24}} < k < - \frac{5}{{24}}\). Vậy chỉ có k = -1 thỏa mãn. Khi đó \(x = - \frac{{7\pi }}{{12}}\). Vậy phương trình có hai nghiệm thuộc khoảng \(( - \pi ;\pi )\) là \(x = - \frac{\pi }{4}\) và \(x = - \frac{{7\pi }}{{12}}\).
Câu 2 :
Cho \(\cos \alpha = - \frac{1}{4}\) và \(\pi < \alpha < \frac{{3\pi }}{2}\). Khi đó a) \({\sin ^2}\alpha = \frac{{15}}{{16}}\)
Đúng
Sai
b) \(\sin \alpha = \frac{{\sqrt {15} }}{4}\)
Đúng
Sai
c) \(\tan \alpha = \sqrt {15} \)
Đúng
Sai
d) \(\cot \alpha = - \frac{1}{{\sqrt {15} }}\)
Đúng
Sai
Đáp án
a) \({\sin ^2}\alpha = \frac{{15}}{{16}}\)
Đúng
Sai
b) \(\sin \alpha = \frac{{\sqrt {15} }}{4}\)
Đúng
Sai
c) \(\tan \alpha = \sqrt {15} \)
Đúng
Sai
d) \(\cot \alpha = - \frac{1}{{\sqrt {15} }}\)
Đúng
Sai
Phương pháp giải :
a) Áp dụng công thức \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) và dựa vào góc phần tư của đường tròn lượng giác để xét dấu. b) Áp dụng công thức \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) và dựa vào góc phần tư của đường tròn lượng giác để xét dấu. c) \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{1}{{\cot \alpha }}\) d) \(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{1}{{\tan \alpha }}\) Lời giải chi tiết :
\({\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Rightarrow {\cos ^2}\alpha = 1 - {\sin ^2}\alpha = 1 - {\left( { - \frac{1}{4}} \right)^2} = \frac{{15}}{{16}} \Rightarrow \sin \alpha = \pm \frac{{\sqrt {15} }}{4}\). Vì \(\pi < \alpha < \frac{{3\pi }}{2}\) nên điểm cuối của cung \(\alpha \) thuộc góc phần tư thứ III nên \(\sin \alpha < 0\). Vậy \(\sin \alpha = - \frac{{\sqrt {15} }}{4}\). \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{ - \frac{1}{4}}}{{ - \frac{{\sqrt {15} }}{4}}} = \sqrt {15} \); \(\cot \alpha = \frac{1}{{\tan \alpha }} = \frac{1}{{\sqrt {15} }}\). a) Đúng. b) Sai. c) Đúng. d) Sai.
Câu 3 :
Cho dãy số \(({u_n})\) biết \({u_n} = {2^n} + 1\). Khi đó a) Dãy số \(({u_n})\) là dãy số tăng
Đúng
Sai
b) Dãy số \(({u_n})\) là dãy số bị chặn
Đúng
Sai
c) \({u_6} = 65\)
Đúng
Sai
d) Số hạng thứ n + 2 của dãy số là \({u_{n + 2}} = {2^n}.2\)
Đúng
Sai
Đáp án
a) Dãy số \(({u_n})\) là dãy số tăng
Đúng
Sai
b) Dãy số \(({u_n})\) là dãy số bị chặn
Đúng
Sai
c) \({u_6} = 65\)
Đúng
Sai
d) Số hạng thứ n + 2 của dãy số là \({u_{n + 2}} = {2^n}.2\)
Đúng
Sai
Phương pháp giải :
a) Dãy số \(({u_n})\) là dãy số giảm nếu \({u_n} > {u_{n + 1}}\). Dãy số \(({u_n})\) là dãy số tăng nếu \({u_n} < {u_{n + 1}}\). b) Dãy số \(({u_n})\) là dãy số bị chặn nếu \(({u_n})\) vừa bị chặn trên vừa bị chặn dưới, tức tồn tại hai số m, M sao cho \(m \le {u_n} \le M\) \(\forall n \in \mathbb{N}*\). c) Tính \({u_6}\) bằng công thức \({u_n} = {2^n} + 1\). d) Thay n + 2 vào n trong công thức số hạng tổng quát \({u_n} = {2^n} + 1\). Lời giải chi tiết :
a) Đúng. \({u_{n + 1}} - {u_n} = {2^{n + 1}} + 1 - ({2^n} + 1) = {2^{n + 1}} - {2^n} = {2^n}(2 - 1) = {2^n} > 0\) với mọi n. Vậy dãy số là dãy tăng. b) Sai. Dãy không bị chặn trên vì không có giá trị M nào để \({2^n} < M\) với mọi n. Vậy dãy số không bị chặn. c) Đúng. \({u_6} = {2^6} + 1 = 64 + 1 = 65\). d) Sai. \({u_{n + 2}} = {2^{n + 2}} + 1 = {4.2^n} + 1\).
Câu 4 :
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Mặt phẳng (P) qua BD và song song với SA. Khi đó a) Giao tuyến của hai mặt phẳng (SAB) và (SAD) là SO
Đúng
Sai
b) SO thuộc mặt phẳng (SBD)
Đúng
Sai
c) Gọi I là giao điểm của SC và (P). Khi đó OI//SA
Đúng
Sai
d) Thiết diện giữa (P) và hình chóp là hình bình hành
Đúng
Sai
Đáp án
a) Giao tuyến của hai mặt phẳng (SAB) và (SAD) là SO
Đúng
Sai
b) SO thuộc mặt phẳng (SBD)
Đúng
Sai
c) Gọi I là giao điểm của SC và (P). Khi đó OI//SA
Đúng
Sai
d) Thiết diện giữa (P) và hình chóp là hình bình hành
Đúng
Sai
Phương pháp giải :
Sử dụng các định lý về đường thẳng song song với mặt phẳng, cách tìm giao tuyến, thiết diện của hai mặt phẳng. Lời giải chi tiết :
a) Sai. Giao tuyến của hai mặt phẳng (SAB) và (SAD) là SA. b) Đúng. SO thuộc mặt phẳng (SBD) vì cả \(S \in (SBD)\), \(O \in BD \subset (SBD)\). c) Đúng. Có \(OI \subset (P)\) mà SA//(P) nên SA không cắt đường thẳng nào trong (P), tức OI//SA (do OI, SA cùng thuộc mặt phẳng (SAC)). d) Sai. Thiết diện là tam giác BID.
Phần III: Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1 :
Hằng ngày mực nước tại một cảng biển lên xuống theo thủy triều. Độ sâu h (m) của mực nước theo thời gian t (giờ) trong một ngày được cho bởi công thức \(h = 11 + 2\sin \left( {\frac{\pi }{{12}}t} \right)\) với \(0 \le t \le 24\). Tính thời điểm mực nước tại cảng cao nhất. Đáp án: Đáp án
Đáp án: Phương pháp giải :
Tìm t sao cho hàm số \(h = 11 + 2\sin \left( {\frac{\pi }{{12}}t} \right)\) đạt giá trị lớn nhất. Lời giải chi tiết :
\(h = 11 + 2\sin \left( {\frac{\pi }{{12}}t} \right)\) đạt giá trị lớn nhất khi \(\sin \left( {\frac{\pi }{{12}}t} \right) = 1 \Leftrightarrow \frac{\pi }{{12}}t = \frac{\pi }{2} + k2\pi \Leftrightarrow t = 6 + 24k\) (giờ). Vì \(0 \le t \le 24\) nên chỉ có giá trị t = 6 thỏa mãn. Vậy thời điểm mực nước tại cảng cao nhất là lúc 6 giờ.
Câu 2 :
Phương trình \(2\sin 2x + 4\cos x = 0\) có bao nhiêu nghiệm trong khoảng (0;3000)? Đáp án: Đáp án
Đáp án: Phương pháp giải :
Giải phương trình lượng giác bằng cách biến đổi về dạng phương trình tích. Xét họ nghiệm trong khoảng (0;3000) để tìm số giá trị k nguyên thỏa mãn. Lời giải chi tiết :
Ta có: \(2\sin 2x + 4\cos x = 0 \Rightarrow 4\sin x.\cos x + 4\cos x = 0 \Rightarrow 4\cos x.(\sin x + 1) = 0\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\cos x = 0}\\{\sin x = - 1}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{2} + k\pi }\\{x = \frac{{3\pi }}{2} + k2\pi }\end{array}} \right. \Leftrightarrow x = \frac{\pi }{2} + k\pi \) với \(k \in \mathbb{Z}\). Xét họ nghiệm \(x = \frac{\pi }{2} + k\pi \), ta có: \(0 < \frac{\pi }{2} + k\pi < 3000 \Leftrightarrow - \frac{\pi }{2} < k\pi < 3000 - \frac{\pi }{2} \Leftrightarrow - \frac{1}{2} < k < \frac{{3000}}{\pi } - \frac{1}{2} \Leftrightarrow - 0,5 < k < 954,43\). Mà \(k \in \mathbb{Z}\) nên \(k \in \{ 0;1;2;3;...;954\} \), tức có 955 giá trị k thỏa mãn. Vậy phương trình có 955 nghiệm thuộc khoảng (0;3000).
Câu 3 :
Công ty cây xanh X trồng 496 cây hoa trong một khu vườn hình tam giác như sau: hàng thứ nhất trồng 1 cây hoa, kể từ hàng thứ hai trở đi số cây hoa trồng mỗi hàng nhiều hơn 1 cây so với hàng liền trước nó. Hỏi công ty cây xanh X trồng được bao nhiêu hàng cây trong khu vườn hình tam giác đó. Đáp án: Đáp án
Đáp án: Phương pháp giải :
Số cây mỗi hàng lập thành một cấp số cộng với tổng n số hạng là 496, số hạng đầu \({u_1} = 1\) công sai d = 1. Tìm n. Lời giải chi tiết :
Số cây mỗi hàng lập thành một cấp số cộng với tổng n số hạng là 496, số hạng đầu \({u_1} = 1\) công sai d = 1. Ta có: \(496 = \frac{{2.1 + (n - 1).1}}{2}.n \Leftrightarrow 992 = (2 + n - 1).n = {n^2} + n - 992 = 0\). Ta tính được n = 31 hoặc n = -32 (loại). Vậy số hàng cây trồng được là 31 hàng.
Câu 4 :
Cho dãy số \(({u_n})\) biết \({u_n} = n + \frac{1}{n}\). Tìm m để dãy số \(({u_n})\) bị chặn dưới bởi m. Đáp án: Đáp án
Đáp án: Phương pháp giải :
Chứng minh dãy số tăng và bị chặn dưới tại \(m = {u_1}\). Lời giải chi tiết :
Xét \({u_{n + 1}} - {u_n} = \left( {n + 1 + \frac{1}{{n + 1}}} \right) - \left( {n + \frac{1}{n}} \right) = 1 + \frac{1}{{n + 1}} - \frac{1}{n} = \left( {1 - \frac{1}{n}} \right) + \frac{1}{{n + 1}}\). Ta có: \(n \ge 1 \Leftrightarrow \frac{1}{n} < 1 \Leftrightarrow 1 - \frac{1}{n} > 0\); \(n \ge 1 \Rightarrow \frac{1}{{n + 1}} > 0\). Vậy \({u_{n + 1}} - {u_n} > 0\), tức dãy số tăng. Khi đó, dãy bị chặn dưới bởi \({u_1} = 1 + \frac{1}{1} = 2 = m\).
Câu 5 :
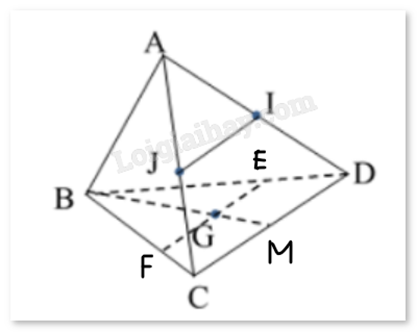
Cho tứ diện ABCD. Điểm I và J theo thức tự là trung điểm của AD và AC, G là trọng tâm tam giác BCD. Giao tuyến của hai mặt phẳng (GIJ) và (BCD) cắt BD tại E, cắt BC tại F. Tính tỉ số \(\frac{{IJ}}{{EF}}\) (Viết dưới dạng số thập phân)? Đáp án: Đáp án
Đáp án: Phương pháp giải :
Sử dụng định lý giao tuyến của ba mặt phẳng, định lý Thales. Lời giải chi tiết :
Xét \(\Delta ACD\) có IJ//CD suy ra \(\frac{{AI}}{{AD}} = \frac{{AJ}}{{AC}} = \frac{1}{2}\) (I và J theo thức tự là trung điểm của AD và AC). Từ đó dễ dàng chứng minh \(\Delta AIJ\)ᔕ \(\Delta ADC\), suy ra \(\frac{{IJ}}{{CD}} = \frac{1}{2}\), tức \(IJ = \frac{1}{2}CD\) (1) Ta có: \(\left\{ {\begin{array}{*{20}{c}}{CD = (ACD) \cap (BCD)}\\{IJ = (ACD) \cap (IJG)}\\{EF = (IJG) \cap (BCD)}\\{IJ/CD}\end{array}} \right.\). Theo định lý về giao tuyến của ba mặt phẳng, ta được: EF//CD//IJ. Vì \(\left\{ {\begin{array}{*{20}{c}}{EF = (IJG) \cap (BCD)}\\\begin{array}{l}G \in (IJG)\\G \in (BCD)\end{array}\end{array}} \right.\) nên E, G, F thẳng hàng. Xét \(\Delta BCM\) có FG//CM (vì EF//CD) suy ra \(\frac{{BF}}{{BC}} = \frac{{BG}}{{BM}} = \frac{2}{3}\) (vì G là trọng tâm \(\Delta BCD\)). Xét \(\Delta BCD\) có EF//CD suy ra \(\frac{{BF}}{{BC}} = \frac{{BE}}{{BD}} = \frac{2}{3}\). Từ đó dễ dàng chứng minh \(\Delta BEF\)ᔕ\(\Delta BDC\), suy ra \(\frac{{EF}}{{CD}} = \frac{2}{3}\), tức \(EF = \frac{2}{3}CD\) (2) Từ (1) và (2) suy ra \(\frac{{IJ}}{{EF}} = \frac{{\frac{1}{2}CD}}{{\frac{2}{3}CD}} = \frac{3}{4} = 0,75\).
Câu 6 :
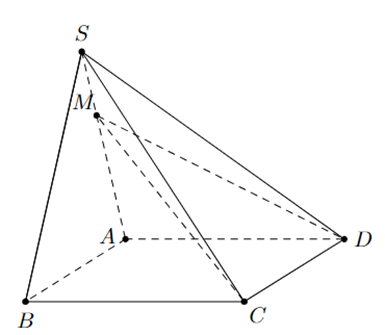
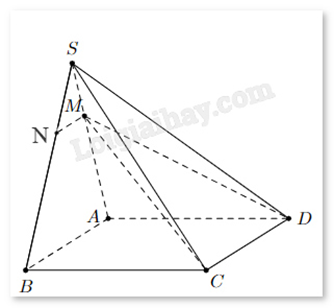
Cho hình chóp S.ABCD có đáy hình bình hành. Trên cạnh SA lấy điểm M sao cho MA = 2MS. Mặt phẳng (CDM) cắt SB tại N. Biết rằng AB = 3 cm, tính tổng MN + CD.
Đáp án: Đáp án
Đáp án: Phương pháp giải :
- Định lý Thales. - Quy tắc tìm giao tuyến của hai mặt phẳng chứa hai đường thẳng song song. Lời giải chi tiết :
Ta có: \(\left\{ {\begin{array}{*{20}{c}}{M \in (CDM)}\\\begin{array}{l}M \in AB \subset (SAB)\\AB//CD\\AB \subset (SAB),CD \subset (CDM)\end{array}\end{array}} \right.\) nên giao tuyến của (CDM) và (SAB) là đường thẳng d song song với AB, CD và đi qua M. Giả sử d cắt SA tại N thì đường thẳng MN là giao tuyến của (CDM), (SAB) và MN//AB, suy ra \(\frac{{SM}}{{SA}} = \frac{{SN}}{{SB}} = \frac{1}{3}\). Từ đó, dễ dàng chứng minh \(\Delta SMN\)ᔕ\(\Delta SAB\), suy ra \(\frac{{MN}}{{AB}} = \frac{1}{3}\), tức \(MN = \frac{1}{3}AB = \frac{1}{3}.3 = 1\) (cm). Vì ABCD là hình bình hành nên AB = CD = 3 (cm). Vậy MN + CD = 1 + 3 = 4 (cm).
|