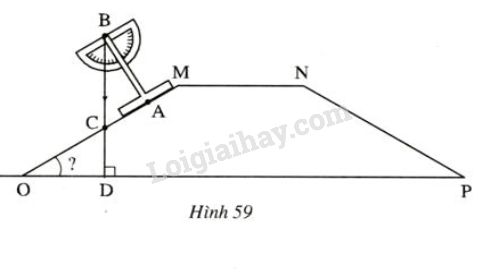
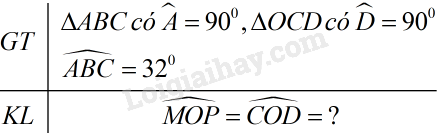Bài 9 trang 109 SGK Toán 7 tập 1

Đề bài

Hình 59 biểu diễn mặt cắt ngang  của một con đê để đo góc nhọn $MOP$ tạo bởi mặt phẳng nghiêng của con đê với phương nằm ngang, người ta dùng thước chữ $T$ và đặt như hình vẽ ($OA\perp AB$). Tính góc $MOP$, biết rằng dây dọi $BC$ tạo với trục $BA$ một góc $\widehat{ABC }= 32^0$ 

Lời giải chi tiết

Tam giác $ABC$ vuông tại $A$ nên $\widehat{ABC}+ \widehat{ACB}= 90^0$ (1) (trong tam giác vuông có hai góc nhọn phụ nhau)

Tam giác $DOC$ vuông tại $D$ nên $\widehat{COD}+ \widehat{OCD}= 90^0$ (2) (trong tam giác vuông có hai góc nhọn phụ nhau) 

Ta lại có $\widehat{ACB}=\widehat{OCD}$ (hai góc đối đỉnh)    (3)

Từ (1), (2), (3) suy ra $\widehat{COD}= \widehat{ABC}=32^0$.

Vậy $\widehat{MOP}=\widehat{COD}=32^0$

HocTot.Nam.Name.Vn