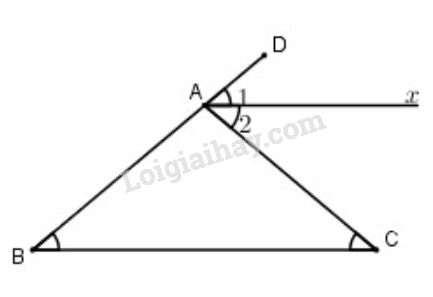
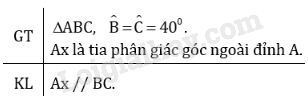Bài 8 trang 109 SGK Toán 7 tập 1

Đề bài

 Cho tam giác $ABC$ có $\widehat{B}=\widehat{C}= 40^0$. Gọi $Ax$ là tia phân giác của góc ngoài ở đỉnh $A$, Hãy chứng tỏ $Ax// BC$. 

Lời giải chi tiết

Cách 1:

Gọi $\widehat{CAD}$ là góc ngoài tại đỉnh $A$ của tam giác $ABC$.

Ta có: $\widehat{CAD }  =  \widehat{B}+ \widehat{C}$$=  40^0+ 40^0=80^0$ ( Góc ngoài bằng tổng 2 góc trong không kề với nó)

Lại có, $Ax$ là phân giác $\widehat{CAD }$

nên $\widehat{A_{2} }= \dfrac{1}2\widehat{CAD}=\dfrac{80^0}2=40^0$

$\Rightarrow \widehat {{A_2}}=\widehat{BCA }(=40^o$)

Mà hai góc này ở vị trí so le trong nên $Ax// BC$.

Cách 2:

Gọi $\widehat{CAD}$ là góc ngoài tại đỉnh $A$ của tam giác $ABC$ 

$\Rightarrow \widehat{CAD }  =  \widehat{B}+ \widehat{C} = 2.\widehat{B}$ ( vì $\widehat{B}= \widehat{C}$)

Mà $Ax$ là phân giác $\widehat{CAD }$ nên $\widehat{CAD} = 2. \widehat{DAx}$

$\Rightarrow \widehat{CAD } = \widehat{DAx}$

Mà 2 góc này ở vị trí đồng vị

$\Rightarrow Ax// BC$