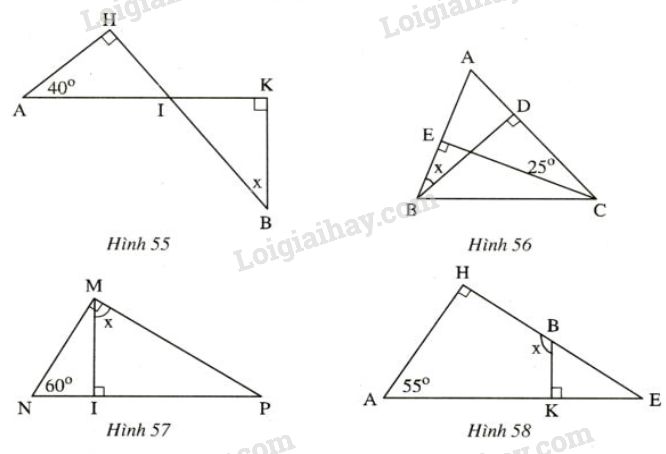
Bài 6 trang 109 SGK Toán 7 tập 1Tìm các số đo x ở các hình sau: Đề bài Tìm các số đo xx ở các hình sau:
Video hướng dẫn giải Phương pháp giải - Xem chi tiết Áp dụng: - Trong tam giác vuông có hai góc nhọn phụ nhau. - Mỗi góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó. Lời giải chi tiết Hình 55) Xét ΔAHI có ˆH=900 ta có: ˆA+^AIH=900 (1) (tổng hai góc nhọn của tam giác vuông bằng 90 độ) Xét ΔBKI có ˆK=900 ta có: ˆB+^BIK=900 (2) (tổng hai góc nhọn của tam giác vuông bằng 90 độ) Từ (1) và (2) suy ra: ˆA+^AIH=ˆB+^BIK Mà ^AIH=^BIK (hai góc đối đỉnh) Nên suy ra ˆB=ˆA=400 Vậy ˆB=x=400 Hình 56) Xét ΔABD có ^ADB=900 ta có: ^ABD+ˆA=900 (4) (tổng hai góc nhọn của tam giác vuông bằng 90 độ) Xét ΔACE có ^AEC=900 ta có: ^ACE+ˆA=900 (5) (tổng hai góc nhọn của tam giác vuông bằng 90 độ) Từ (4) và (5) suy ra ^ACE=^ABD=250 Vậy x=250 Hình 57) Ta có: ^NMP=^NMI+^PMI=900 (6) Xét ΔMNI có ^MIN=900 ta có : ˆN+^NMI=900 (7) (tổng hai góc nhọn của tam giác vuông bằng 90 độ) Từ (6) và (7) suy ra ˆN=^PMI=600 Vậy x=600 Hình 58) Xét ΔAHE có ^AHE=900 ta có : ˆE+ˆA=900 (tổng hai góc nhọn của tam giác vuông bằng 90 độ) ˆE=900−ˆA=900−550=350 Vì ^KBH là góc ngoài tại đỉnh B của tam giác BKE nên ^KBH=^BKE+ˆE=900+350=1250 Vậy x=1250 HocTot.Nam.Name.Vn
>> Học trực tuyến lớp 7 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
|