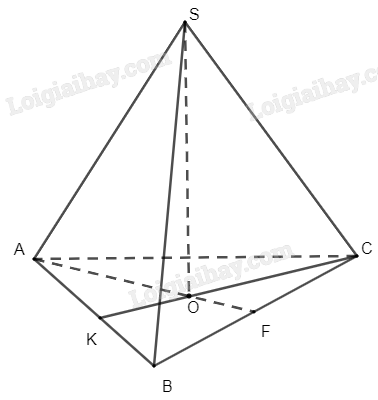
Bài 8.21 trang 79 SGK Toán 11 tập 2 - Cùng khám pháCho hình chóp tam giác đều S.ABC có cạnh bên bằng 4a và cạnh đáy bằng 6a. Tính khoảng cách từ S đến mặt phẳng (ABC). Đề bài Cho hình chóp tam giác đều S.ABC có cạnh bên bằng 4a và cạnh đáy bằng 6a. Tính khoảng cách từ S đến mặt phẳng (ABC). Phương pháp giải - Xem chi tiết Tìm khoảng cách giữa M và (P): + Tìm (Q) chứa M và vuông góc với (P) theo giao tuyến d. + Từ M hạ MH vuông góc với d (H thuộc d). + Khi đó MH là khoảng cách cần tìm. Lời giải chi tiết
Gọi O là trọng tâm tam giác ABC Ta có: BC \(\bot\) AF, BC \(\bot\) SF \(\Rightarrow\) BC \(\bot\) (SAF). Do đó, BC \(\bot\) SO (1) Tương tự, AB \(\bot\) (SCK). Suy ra, AB \(\bot\) SO (2) Từ (1) và(2), SO \(\bot\) (ABC) Vậy d(S,(ABC)) = SO \(\begin{array}{l}AH = 3\sqrt 3 a\\AO = \frac{2}{3}AH = 2\sqrt 3 \\SO = \sqrt {S{A^2} - A{O^2}} = 2a\end{array}\)  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
