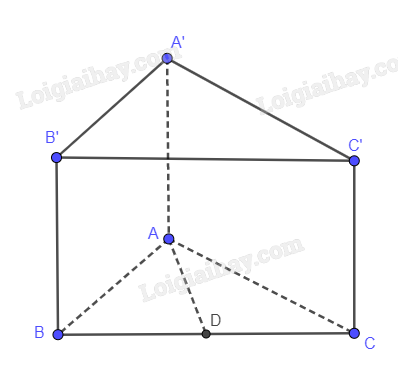
Bài 8.24 trang 79 SGK Toán 11 tập 2 - Cùng khám pháCho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác ABC vuông tại A, có BC = 2a, AB = (sqrt 3 a). Đề bài Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác ABC vuông tại A, có BC = 2a, AB = \(\sqrt 3 a\). Tính khoảng cách giữa AA’ và mặt phẳng (BCC’B’). Phương pháp giải - Xem chi tiết Cho đường thẳng d // (P); để tính khoảng cách giữa d và (P) ta thực hiện các bước: + Chọn một điểm A trên d, sao cho khoảng cách từ A đến (P) có thể được xác định dễ nhất. + Kết luận: d(d; (P)) = d(A; (P)). Lời giải chi tiết
Kẻ AD vuông góc với BC Ta có: AA’ // BB’ nên AA’ // (BCC’B’) \(d\left( {AA',\left( {BCC'B'} \right)} \right) = d\left( {A,\left( {BCC'B'} \right)} \right) = AD\) Xét tam giác ABC vuông tại A có đường cao AD: \(\begin{array}{l}AD.BC = AB.AC\\ \Rightarrow AD = \frac{{a\sqrt 3 .a}}{{2a}} = \frac{{a\sqrt 3 }}{2}\end{array}\)  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
