Trắc nghiệm Bài 7: Tam giác cân Toán 7 Cánh diềuĐề bài
Câu 1 :
Cho tam giác ABC cân tại A có: ˆA=1000,BC=a,AC=b. Về phía ngoài tam giác ABC vẽ tam giác ABD cân tại D có: ^ADB=1400. Tính chu vi tam giác ABD theo a và b.
Câu 2 :
Cho tam giác ABC cân tại A có ˆA=1200,BC=6cm. Đường vuông góc với AB tại A cắt BC ở D. Độ dài BD bằng:
Câu 3 :
Cho tam giác ABC vuông tại A có ˆB=300. Khi đó:
Câu 4 :
Cho M thuộc đoạn thẳng AB. Trên cùng một nửa mặt phẳng bờ AB, vẽ các tam giác đều AMC,BMD. Gọi E;F theo thứ tự là trung điểm của AD;BC. Tam giác MEF là tam giác gì? Chọn câu trả lời đúng nhất.
Câu 5 :
Cho tam giác ABC có ˆA=60∘. Vẽ ra phía ngoài của tam giác hai tam giác đều AMB và ANC.
Câu 6 :
Cho tam giác ABC có ˆA=120∘. Trên tia phân giác của góc A lấy điểm D sao cho AD=AB+AC. Khi đó tam giác BCD là tam giác gì?
Câu 7 :
Tam giác ABC có ˆA=40∘;ˆB−ˆC=20∘. Trên tia đối của tia AC lấy điểm E sao cho AE=AB. Tính số đo góc CBE.
Câu 8 :
Cho tam giác ABC có M là trung điểm của BC và AM=BC2. Số đo góc BAC là
Câu 9 :
Cho tam giác ABC có ˆA=90∘;AB=AC. Khi đó
Câu 10 :
Cho tam giác ABC cân tại đỉnh A với ˆA=800. Trên hai cạnh AB,AC lần lượt lấy hai điểm D và E sao cho AD=AE. Phát biểu nào sau đây là sai?
Cho tam giác ABC vuông cân ở A. Trên đáy BC lấy hai điểm M,N sao cho BM=CN=AB. Câu 11
Tam giác AMN là tam giác gì?
Câu 12
Tính số đo góc ^MAN.
Câu 13 :
Tính số đo x trên hình vẽ sau: 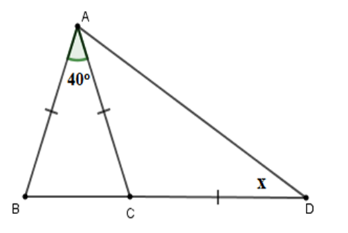
Câu 14 :
Số tam giác cân trong hình vẽ dưới đây là: 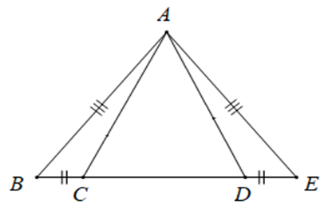
Câu 15 :
Một tam giác cân có góc ở đáy bằng 700 thì số đo góc ở đỉnh là:
Câu 16 :
Một tam giác cân có góc ở đỉnh bằng 640 thì số đo góc ở đáy là:
Câu 17 :
Cho tam giác ABC cân tại A. Phát biểu nào trong các phát biểu sau là sai:
Câu 18 :
Hai góc nhọn của tam giác vuông cân bằng nhau và bằng
Câu 19 :
Chọn câu sai.
Lời giải và đáp án
Câu 1 :
Cho tam giác ABC cân tại A có: ˆA=1000,BC=a,AC=b. Về phía ngoài tam giác ABC vẽ tam giác ABD cân tại D có: ^ADB=1400. Tính chu vi tam giác ABD theo a và b.
Đáp án : C Phương pháp giải :
- Trên cạnh BC lấy điểm E sao cho BE=BD. - Chứng minh ΔBDE đều, suy ra BD=BE=DE=DA. - Chứng minh ΔCAE cân tại C, suy ra AC=EC. - Biểu diễn AD;BD;AB theo a,b. Từ đó tính chu vi của ΔABD. Lời giải chi tiết :
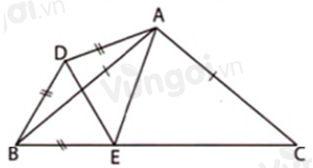 Trên cạnh BC lấy điểm E sao cho BE=BD. ΔABC cân tại A nên ^ABC=180o−^BAC2=180o−100o2=40o. ΔABD cân tại D nên ^DBA=180o−^ADB2=180o−140o2=20o. Ta có: ^DBE=^DBA+^ABC=20o+40o=60o. Xét ΔBDE có: ^DBE=60o nên ΔBDE đều, suy ra BD=BE=DE=DA. ^EDA=^BDA−^BDE=140o−60o=80o ΔDAE cân tại D (vì DA=DE(cmt)) nên ^DEA=^DAE=180o−^EDA2=180o−80o2=50o. ^EAC=^DAB+^BAC−^DAE=20o+100o−50o=70o. ^AEC=180o−^DEA−^DEB=180o−50o−60o=70o. ΔCAE có ^EAC=^AEC=70o nên ΔCAE cân tại C, suy ra AC=EC. Do đó: AD=BD=BE=BC−EC=BC−AC=a−b. AB=AC=b. Vậy chu vi của ΔABD là: AD+BD+AB=a−b+a−b+b=2a−b.
Câu 2 :
Cho tam giác ABC cân tại A có ˆA=1200,BC=6cm. Đường vuông góc với AB tại A cắt BC ở D. Độ dài BD bằng:
Đáp án : C Phương pháp giải :
- Chứng minh ΔADC cân tại D, suy ra DC=DA (1) - Trên cạnh BD lấy E sao cho ^BAE=30o, chứng minh ΔAEB cân tại E, suy ra AE=EB (2) - Chứng minh ΔADE là tam giác đều, suy ra DA=DE=AE (3) - Từ (1), (2) và (3) suy ra: DC=DE=EB=13BC, từ đó ta tính được độ dài BD. Lời giải chi tiết :
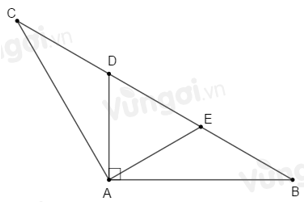 ΔABC cân tại ˆA nên ˆB=ˆC=180o−ˆA2=180o−120o2=30o. Ta có: ^CAD=^BAC−^BAD=120o−90o=30o ΔADC có: ˆC=^CAD=30o nên ΔADC cân tại D, suy ra DC=DA (1) Ta có: ^ADB là góc ngoài tại đỉnh D của ΔADC nên ^ADB=ˆC+^CAD=30o+30o=60o. Trên cạnh BD lấy E sao cho ^BAE=30o thì E nằm giữa B và D. ΔAEB có: ˆB=^BAE=30o nên ΔAEB cân tại E, suy ra AE=EB (2) Ta có: ^DAE=^BAD−^BAE=90o−30o=60o. ΔADE có: ^DAE=^ADE=60o nên ΔADE là tam giác đều, suy ra DA=DE=AE (3) Từ (1), (2) và (3) suy ra: DC=DE=EB=13BC. Do đó BD=DE+EB=23BC=23.6=4(cm).
Câu 3 :
Cho tam giác ABC vuông tại A có ˆB=300. Khi đó:
Đáp án : A Phương pháp giải :
Lấy điểm M trên cạnh BC sao cho ^BAM=30o. Chứng minh ΔAMB cân và ΔAMC đều suy ra MA=MB=MC=AC, từ đó suy ra điều phải chứng minh. Lời giải chi tiết :
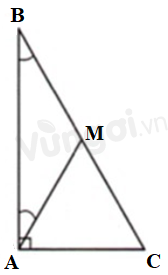 Lấy điểm M trên cạnh BC sao cho ^BAM=30o. ΔAMB có ^BAM=ˆB=30o nên là tam giác cân, suy ra MA=MB (1) ΔABC vuông tại A nên ˆB+ˆC=90o ⇒ˆC=90o−ˆB=90o−30o=60o. Ta có: ^BAC=^BAM+^MAC ⇒^MAC=^BAC−^BAM=90o−30o=60o. ΔAMC có: ^MAC=ˆC=60o nên là tam giác đều, suy ra AC=AM=MC (2) Từ (1) và (2) ta có: AC=MB=MC hay AC=BC2.
Câu 4 :
Cho M thuộc đoạn thẳng AB. Trên cùng một nửa mặt phẳng bờ AB, vẽ các tam giác đều AMC,BMD. Gọi E;F theo thứ tự là trung điểm của AD;BC. Tam giác MEF là tam giác gì? Chọn câu trả lời đúng nhất.
Đáp án : D Phương pháp giải :
- Sử dụng: - Tính chất: Tam giác đều có ba cạnh bằng nhau, ba góc bằng nhau và cùng bằng 60o. - Trường hợp bằng nhau thứ hai của tam giác: Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau. - Dấu hiệu nhận biết tam giác đều: Tam giác cân có một góc bằng 60o. Lời giải chi tiết :
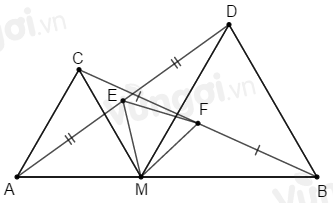 ΔAMC đều nên ^AMC=60o;AM=CM. ΔBMD đều nên ^BMD=60o;MD=MB. ^AMD=^AMC+^CMD=60o+^CMD (1) ^CMB=^BMD+^CMD=60o+^CMD (2) Từ (1) và (2) suy ra: ^AMD=^CMB Xét ΔAMD và ΔCMB có: AM=CM(cmt) ^AMD=^CMB(cmt) MD=MB(cmt) ⇒ΔAMD=ΔCMB(c.g.c) ⇒AD=CB (hai cạnh tương ứng). ⇒^DAM=^BCM (hai góc tương ứng). Xét ΔAEM và ΔCFM có: AM=CM(cmt) ^DAM=^BCM(cmt) AE=CF(AD2=CB2) ⇒ΔAEM=ΔCFM(c.g.c) ⇒EM=FM (hai cạnh tương ứng). ⇒^AME=^CMF (hai góc tương ứng) ⇒^AMC+^CME=^CME+^EMF ⇒^AMC=^EMF ⇒^EMF=60o Xét ΔMEF có: EM=FM(cmt);^EMF=60o(cmt) nên ΔMEF là tam giác đều. Tam giác đều vừa là tam giác cân vừa là tam giác nhọn (vì có ba góc nhọn) nên cả A, B, C đều đúng.
Câu 5 :
Cho tam giác ABC có ˆA=60∘. Vẽ ra phía ngoài của tam giác hai tam giác đều AMB và ANC.
Đáp án : D Phương pháp giải :
+ Ta sử dụng tính chất tam giác cân, tính chất tia phân giác của một góc, tính chất hai góc kề bù để chứng minh các cặp góc so le trong bằng nhau để chứng minh ba điểm M,A,N thẳng hàng. + Chứng minh cạnh bằng nhau ta sử dụng các trường hợp bằng nhau của tam giác để chứng minh hai tam giác bằng nhau từ đó suy ra hai cạnh tương ứng bằng nhau. Lời giải chi tiết :
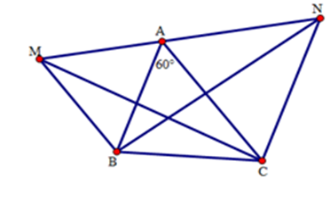 + Các tam giác AMB và ANC là các tam giác đều(gt) nên ^MAB=600,^NAC=600. Ta có: ^MAB+^BAC+^CAN=600+600+600=1800. Suy ra ba điểm M,A,N thẳng hàng. + Ta có: ^MAC=^MAB+^BAC=600+600=1200^BAN=^CAN+^BAC=600+600=1200 Do đó ^MAC=^BAN . Xét hai tam giác ABN và AMC có: +) AB=AM (do tam giác AMB đều) +) ^BAN=^MAC (cmt) +) AN=AC (do tam giác ANC đều) Do đó ΔABN=ΔAMC(c.g.c) Suy ra BN=CM (hai cạnh tương ứng). Vậy cả A, B đều đúng.
Câu 6 :
Cho tam giác ABC có ˆA=120∘. Trên tia phân giác của góc A lấy điểm D sao cho AD=AB+AC. Khi đó tam giác BCD là tam giác gì?
Đáp án : B Phương pháp giải :
Dựa vào tính chất tổng các góc của tam giác và dựa vào tính chất tam giác cân. Lời giải chi tiết :
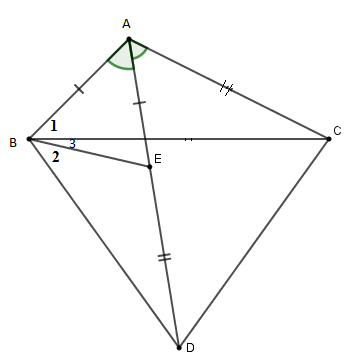 Lấy E∈AD sao cho AE=AB mà AD=AB+AC nên AC=DE. ΔABE cân có ^BAD=60∘ nên ΔABE là tam giác đều suy ra AE=EB. Thấy ^BED=^EBA+^EAB=120∘ (góc ngoài tại đỉnh E của tam giác ABE ) nên ^BED=^BAC(=120∘) Suy ra ΔEBD=ΔABC(c.g.c)⇒^B1=^B2 (hai góc tương ứng bằng nhau) và BD=BC (hai cạnh tương ứng) Lại có ^B1+^B3=60∘ nên ^B2+^B3=60∘. ΔBCD cân tại B có ^CBD=60∘ nên nó là tam giác đều.
Câu 7 :
Tam giác ABC có ˆA=40∘;ˆB−ˆC=20∘. Trên tia đối của tia AC lấy điểm E sao cho AE=AB. Tính số đo góc CBE.
Đáp án : B Phương pháp giải :
Dựa vào tính chất tổng các góc của tam giác và dựa vào tính chất tam giác cân. Lời giải chi tiết :
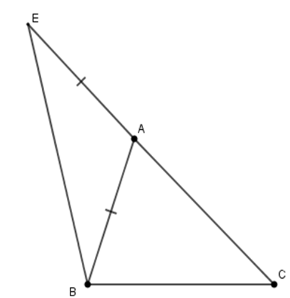 Xét tam giác ABC có ˆA+ˆB+ˆC=180∘ (định lý tổng ba góc trong tam giác) và ˆA=40∘;ˆB−ˆC=20∘(gt) Suy ra ˆB+ˆC=140∘ nên ˆB=140∘+20∘2=80∘;ˆC=60∘ Xét tam giác AEB cân tại A (do AB=AE(gt)) nên ^AEB=^ABE (tính chất) (1) Lại có ^BAC là góc ngoài của tam giác AEB⇒^BAC=^AEB+^ABE (2) Từ (1) và (2) suy ra ^ABE=^BAC2=20∘ Do đó ^CBE=^CBA+^ABE=80∘+20∘=100∘.
Câu 8 :
Cho tam giác ABC có M là trung điểm của BC và AM=BC2. Số đo góc BAC là
Đáp án : C Phương pháp giải :
Dựa vào tính chất tổng các góc của tam giác và dựa vào tính chất tam giác cân. Lời giải chi tiết :
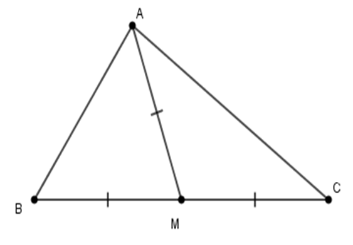 Từ giả thiết suy ra AM=BM=CM Ta có ^BAC+ˆB+ˆC=180∘ (định lý tổng ba góc trong tam giác) (1) Lại có ΔAMB cân tại M(doMA=MB) nên ˆB=^BAM (tính chất) (2) Tương tự ΔAMC cân tại M(doMA=MC) nên ˆC=^MAC (tính chất) (3) Từ (1); (2); (3) ta có ^BAC+^BAM+^CAM=180∘ ⇒^BAC+^BAC=180∘ 2.^BAC=180∘ ⇒^BAC=90∘.
Câu 9 :
Cho tam giác ABC có ˆA=90∘;AB=AC. Khi đó
Đáp án : D Lời giải chi tiết :
Tam giác ABC có ˆA=90∘;AB=AC nên tam giác ABC vuông cân. Tam giác vuông cân là tam giác vừa vuông vừa cân nên cả A, B, C đều đúng.
Câu 10 :
Cho tam giác ABC cân tại đỉnh A với ˆA=800. Trên hai cạnh AB,AC lần lượt lấy hai điểm D và E sao cho AD=AE. Phát biểu nào sau đây là sai?
Đáp án : D Phương pháp giải :
Sử dụng tính chất tam giác cân, tính chất tổng các góc của một tam giác, dấu hiệu nhận biết hai đường thẳng song song. Lời giải chi tiết :
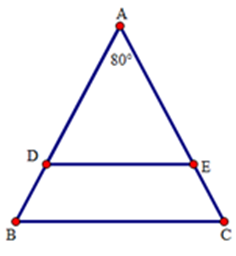 Do tam giác ABC cân nên ˆB=1800−ˆA2=1800−8002=500 Ta thấy tam giác ADE cân do AD=AE. ⇒^ADE=1800−ˆA2=1800−8002=500 Do đó ˆB=^ADE . Mà hai góc này ở vị trí so le trong nên ED//BC. Vậy D là đáp án sai. Cho tam giác ABC vuông cân ở A. Trên đáy BC lấy hai điểm M,N sao cho BM=CN=AB. Câu 11
Tam giác AMN là tam giác gì?
Đáp án : A Phương pháp giải :
Để chứng minh tam giác AMN cân, ta chứng minh hai góc ở đáy bằng nhau ^AMN=^ANM. Lời giải chi tiết :
Do tam giác ABC vuông cân ở A nên ˆB=ˆC=450. Xét tam giác AMB có: BM=BA(gt), nên tam giác AMB cân ở B. Do đó ^AMB=1800−ˆB2=1800−4502=67030′ Chứng minh tương tự ta được tam giác ANC cân ở C và ^ANC=67030′. Xét tam giác AMN có: ^AMN=^ANM=67030′, do đó tam giác AMN cân ở A. Câu 12
Tính số đo góc ^MAN.
Đáp án : A Phương pháp giải :
Dựa vào tính chất tổng các góc của tam giác và dựa vào tính chất tam giác cân. Lời giải chi tiết :
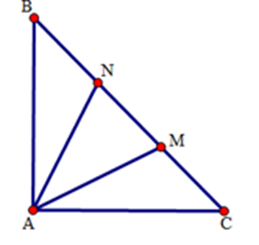 Xét tam giác AMN, ta có: ^MAN=1800−(^AMN+^ANM)=1800−1350=450. Vậy ^MAN=450.
Câu 13 :
Tính số đo x trên hình vẽ sau: 
Đáp án : C Phương pháp giải :
Sử dụng tính chất tổng ba góc của một tam giác, tính chất góc ngoài và sử dụng tính chất của tam giác cân. Lời giải chi tiết :
Tam giác ABC cân tại A (vì AB=AC ) có ˆA=40∘ nên ˆB=^ACB=180∘−40∘2=70∘ Mà ^ACB là góc ngoài của tam giác ACD nên ^ACB=^CAD+^CDA Lại có ΔCAD cân tại C⇒^CAD=^CDA=x (tính chất) Nên ^ACB=^CAD+^CDA=2x⇒x=^ACB2=70∘2=35∘. Vậy x=35∘.
Câu 14 :
Số tam giác cân trong hình vẽ dưới đây là: 
Đáp án : A Lời giải chi tiết :
Từ hình vẽ ta có AB=AE;BC=DE Vì AB=AE⇒ΔABE cân tại A. Suy ra ˆB=ˆE (hai góc ở đáy) Xét tam giác ABC và AED có: AB=AE;ˆB=ˆE(cmt);BC=DE nên ΔABC=ΔAED(c−g−c) Do đó AC=AD (hai cạnh tương ứng) suy ra ΔACD cân tại A. Vậy có hai tam giác cân trên hình vẽ.
Câu 15 :
Một tam giác cân có góc ở đáy bằng 700 thì số đo góc ở đỉnh là:
Đáp án : D Phương pháp giải :
Sử dụng tính chất tổng ba góc của một tam giác và sử dụng tính chất của tam giác cân. Lời giải chi tiết :
Tổng số đo hai góc ở đáy là 70o.2=140∘ Vì tổng ba góc của tam giác bằng 180∘ nên số đo góc ở đỉnh tam giác cân này là 180∘−140∘=40∘.
Câu 16 :
Một tam giác cân có góc ở đỉnh bằng 640 thì số đo góc ở đáy là:
Đáp án : B Phương pháp giải :
Sử dụng tính chất tổng ba góc của một tam giác và sử dụng tính chất của tam giác cân. Lời giải chi tiết :
Sử dụng cách tính số đo các góc trong tam giác ABC cân tại A. Góc ở đỉnh ˆA=1800−2ˆC và góc ở đáy ˆC=1800−ˆA2. Áp dụng ta có số đo góc ở đáy bằng: 1800−6402=580
Câu 17 :
Cho tam giác ABC cân tại A. Phát biểu nào trong các phát biểu sau là sai:
Đáp án : D Phương pháp giải :
+ Áp dụng tính chất của tam giác cân và tính chất tổng các góc của một tam giác Lời giải chi tiết :
Do tam giác ABC cân nên ˆB=ˆC Xét tam giác ABC ta có: ˆA+ˆB+ˆC=1800⇔ˆB+ˆC=1800−ˆA⇔ˆC=1800−ˆA2 hay ˆA=1800−2ˆC Chú ý
Từ kết quả trên ta có cách tính số đo các góc trong tam giác ABC cân tại A. Góc ở đỉnh ˆA=1800−2ˆC và góc ở đáy ˆC=1800−ˆA2.
Câu 18 :
Hai góc nhọn của tam giác vuông cân bằng nhau và bằng
Đáp án : B Lời giải chi tiết :
Mỗi góc nhọn của tam giác vuông cân bằng {45^0}.
Câu 19 :
Chọn câu sai.
Đáp án : C Lời giải chi tiết :
Tam giác đều là tam giác có ba cạnh bằng nhau. Trong tam giác đều, mỗi góc bằng {60^0}. Nên A, B đúng. Tam giác đều cũng là tam giác cân nhưng tam giác cân chưa chắc là tam giác đều vì nó chỉ có hai cạnh bên bằng nhau. Vậy C sai.
|












