Bài tập trắc nghiệm Toán 7 - Chân trời sáng tạo

Trắc nghiệm Bài 1: Tập hợp các số hữu tỉ Toán 7 Chân trời sáng tạo

Làm đề thi

Đề bài

Câu 1 :

Tập hợp các số hữu tỉ được kí hiệu là:

A

$\mathbb{R}$
B

$\mathbb{Q}$
C

$\mathbb{I}$
D

$\mathbb{N}$

Câu 2 :

Khẳng định nào sau đây là đúng?

A

Nếu a > b thì –a > - b
B

Nếu a < b, a < c thì b < c
C

Nếu a < b; c > b thì a < c
D

Số hữu tỉ gồm: số hữu tỉ dương và số hữu tỉ âm

Câu 3 :

Trong các phân số sau, phân số nào biểu diễn số hữu tỉ -0,35

A

$- \frac{3}{5}$
B

$\frac{7}{{20}}$
C

- $\frac{7}{{20}}$
D

$\frac{{ - 35}}{{10}}$

Câu 4 :

Biểu diễn các số: $- 0,4;\frac{8}{{20}};\frac{{12}}{{ - 20}};\frac{{ - 3}}{8}; - 0,375$ bởi các điểm trên cùng một trục số ta được bao nhiêu điểm phân biệt?

A

5
B

4
C

3
D

2

Câu 5 :

Sắp xếp các số hữu tỉ $\frac{{ - 7}}{{20}};\frac{5}{{ - 20}};\frac{{ - 5}}{{17}};\frac{1}{{ - 3}}$ theo thứ tự giảm dần:

A

$\frac{5}{{ - 20}};\frac{{ - 5}}{{17}};\frac{1}{{ - 3}};\frac{{ - 7}}{{20}}$
B

$\frac{{ - 7}}{{20}};\frac{5}{{ - 20}};\frac{{ - 5}}{{17}};\frac{1}{{ - 3}}$
C

$\frac{{ - 7}}{{20}};\frac{1}{{ - 3}};\frac{{ - 5}}{{17}};\frac{5}{{ - 20}}$
D

$\frac{1}{{ - 3}};\frac{{ - 5}}{{17}};\frac{5}{{ - 20}};\frac{{ - 7}}{{20}}$

Câu 6 :

Cho $x = \frac{a}{{2{a^2} + 1}}$

Với giá trị nào của a thì x là số hữu tỉ dương?

A

a < 0
B

a > 0
C

a = 0
D

a $\ge$ 0

Câu 7 :

Có mấy giá trị x nguyên thỏa mãn: $\frac{{9}}{{ - 21}} > \frac{x}{7} > \frac{{ - 11}}{{14}}$

A

0
B

2
C

4
D

6

Câu 8 :

Thành tích chạy thi 100 m của 4 bạn An, Bình, Chi, Duy lần lượt là: 21,54 giây; $\frac{1}{3}$ phút; $\frac{{108}}{5}$ giây; $20\frac{3}{8}$ giây.

Hỏi bạn nào chạy nhanh nhất?

A

An
B

Bình
C

Chi
D

Duy

Câu 9 :

Cho số hữu tỉ $x = \frac{7}{{n + 2}}$

Tìm tổng của các số nguyên n sao cho x là một số nguyên

A

-4
B

4
C

0
D

-8

Câu 10 :

Số $\dfrac{9}{4}$ có số đối là:

A

$\dfrac{4}{9}$
B

$\dfrac{{ - 4}}{9}$
C

$\dfrac{9}{{ - 4}}$
D

$2,25$

Lời giải và đáp án

Câu 1 :

Tập hợp các số hữu tỉ được kí hiệu là:

A

$\mathbb{R}$
B

$\mathbb{Q}$
C

$\mathbb{I}$
D

$\mathbb{N}$

Đáp án : B

Phương pháp giải :

Kí hiệu các tập hợp số

Lời giải chi tiết :

Tập hợp các số hữu tỉ được kí hiệu là: Q

Chú ý

Kí hiệu Q của tập hợp các số hữu tỉ được coi như là chữ viết tắt của quoziente, nghĩa là tỷ lệ

Câu 2 :

Khẳng định nào sau đây là đúng?

A

Nếu a > b thì –a > - b
B

Nếu a < b, a < c thì b < c
C

Nếu a < b; c > b thì a < c
D

Số hữu tỉ gồm: số hữu tỉ dương và số hữu tỉ âm

Đáp án : C

Phương pháp giải :

Tính chất, thứ tự trên tập hợp các só hữu tỉ

Lời giải chi tiết :

+) Nếu a > b thì –a < -b nên A sai

+) Nếu a < b, a < c thì chưa thể so sánh được b với c nên B sai

+) Nếu a < b, c > b ( hay b < c) thì a < c ( tính chất bắc cầu) nên C đúng

+) Số hữu tỉ gồm: số hữu tỉ âm, số hữu tỉ dương và số 0 nên D sai.

Câu 3 :

Trong các phân số sau, phân số nào biểu diễn số hữu tỉ -0,35

A

$- \frac{3}{5}$
B

$\frac{7}{{20}}$
C

- $\frac{7}{{20}}$
D

$\frac{{ - 35}}{{10}}$

Đáp án : C

Phương pháp giải :

Biểu diễn số thập phân dưới dạng phân số:

+ Viết số thập phân dưới dạng phân số có mẫu số là lũy thừa của 10

+ Rút gọn phân số.

Lời giải chi tiết :

Ta có:

$- 0,35 = \frac{{ - 35}}{{100}} = \frac{{( - 35):5}}{{100:5}} = \frac{{ - 7}}{{20}}$

Câu 4 :

Biểu diễn các số: $- 0,4;\frac{8}{{20}};\frac{{12}}{{ - 20}};\frac{{ - 3}}{8}; - 0,375$ bởi các điểm trên cùng một trục số ta được bao nhiêu điểm phân biệt?

A

5
B

4
C

3
D

2

Đáp án : B

Phương pháp giải :

+ Đưa các số về dạng phân số tối giản rồi xác định các số bằng nhau.

+ Các số bằng nhau chỉ được biểu diễn bởi một điểm trên trục số.

Lời giải chi tiết :

Ta có:

$\begin{array}{l} - 0,4 = \frac{{ - 4}}{{10}} = \frac{{ - 4:2}}{{10:2}} = \frac{{ - 2}}{5};\\\frac{8}{{20}} = \frac{{8:4}}{{20:4}} = \frac{2}{5};\\\frac{{12}}{{ - 20}} = \frac{{12:( - 4)}}{{( - 20):( - 4)}} = \frac{{ - 3}}{5};\\\frac{{ - 3}}{8};\\ - 0,375 = \frac{{ - 375}}{{1000}} = \frac{{( - 375):125}}{{1000:125}} = \frac{{ - 3}}{8}\end{array}$

Ta có các điểm biểu diễn khác nhau là $\frac{{ - 2}}{5}; \frac{2}{5}; \frac{{ - 3}}{5}; \frac{{ - 3}}{8}$

Vậy các số trên biểu diễn 4 số hữu tỉ khác nhau nên được biểu diễn bởi 4 điểm khác nhau trên trục số

Câu 5 :

Sắp xếp các số hữu tỉ $\frac{{ - 7}}{{20}};\frac{5}{{ - 20}};\frac{{ - 5}}{{17}};\frac{1}{{ - 3}}$ theo thứ tự giảm dần:

A

$\frac{5}{{ - 20}};\frac{{ - 5}}{{17}};\frac{1}{{ - 3}};\frac{{ - 7}}{{20}}$
B

$\frac{{ - 7}}{{20}};\frac{5}{{ - 20}};\frac{{ - 5}}{{17}};\frac{1}{{ - 3}}$
C

$\frac{{ - 7}}{{20}};\frac{1}{{ - 3}};\frac{{ - 5}}{{17}};\frac{5}{{ - 20}}$
D

$\frac{1}{{ - 3}};\frac{{ - 5}}{{17}};\frac{5}{{ - 20}};\frac{{ - 7}}{{20}}$

Đáp án : A

Phương pháp giải :

+ Dùng tính chất: Nếu a < b thì –a > - b

+ Các phân số có cùng mẫu số dương: phân số nào có tử số lớn hơn thì phân số đó lớn hơn

+ Các phân số dương có cùng tử số: phân số nào có mẫu số lớn hơn thì nhỏ hơn

Lời giải chi tiết :

+ So sánh $\frac{5}{{ - 20}}$ và $\frac{{ - 5}}{{17}}$ :

Vì 20 > 17 nên $\frac{5}{{20}} < \frac{5}{{17}}$ , do đó $\frac{5}{{ - 20}} > \frac{{ - 5}}{{17}}$

+ So sánh $\frac{ - 5}{17}$ và $\frac{1}{{ - 3}}$ :

Vì $\frac{5}{{17}} < \frac{5}{{15}}$ nên $\frac{{ - 5}}{{17}} > \frac{{ - 5}}{{15}} = \frac{1}{{ - 3}}$

+ So sánh $\frac{1}{ - 3}$ và $\frac{{ - 7}}{{20}}$ :

Vì $\frac{7}{{20}} > \frac{7}{{21}}$ nên $\frac{{ - 7}}{{20}} < \frac{{ - 7}}{{21}} = \frac{1}{{ - 3}}$

Do đó, $\frac{5}{{ - 20}} > \frac{{ - 5}}{{17}} > \frac{1}{{ - 3}} > \frac{{ - 7}}{{20}}$

Câu 6 :

Cho $x = \frac{a}{{2{a^2} + 1}}$

Với giá trị nào của a thì x là số hữu tỉ dương?

A

a < 0
B

a > 0
C

a = 0
D

a $\ge$ 0

Đáp án : B

Phương pháp giải :

Số hữu tỉ $\frac{a}{b}$ là số hữu tỉ dương khi a, b cùng dấu

Nhận xét về mẫu số của phân số

Lời giải chi tiết :

$x = \frac{a}{{2{a^2} + 1}}$ là số hữu tỉ dương thì $x = \frac{a}{{2{a^2} + 1}} > 0$

Ta có:

a² $\ge$ 0, với mọi a nên 2a² + 1 $\ge$ 1 > 0, với mọi a

Như vậy, để $x = \frac{a}{{2{a^2} + 1}}$ > 0 thì a > 0

Câu 7 :

Có mấy giá trị x nguyên thỏa mãn: $\frac{{9}}{{ - 21}} > \frac{x}{7} > \frac{{ - 11}}{{14}}$

A

0
B

2
C

4
D

6

Đáp án : B

Phương pháp giải :

Đưa về các phân số có cùng mẫu số dương rồi so sánh tử số, suy ra điều kiện của x

Lời giải chi tiết :

Ta có:

$\begin{array}{l}\frac{{9}}{{ - 21}} > \frac{x}{7} > \frac{{ - 11}}{{14}}\\ \frac{{ - 3}}{7} > \frac{x}{7} > \frac{{ - 11}}{{14}}\\ \frac{{ - 6}}{{14}} > \frac{{2x}}{{14}} > \frac{{ - 11}}{{14}}\\ - 6 > 2x > - 11\\ - 3 > x > - \frac{{11}}{2}\end{array}$

$- 3 > x > - 5,5$

Mà x nguyên nên $x \in \{ - 4; - 5\}$

Vậy có 2 giá trị x thỏa mãn

Câu 8 :

Thành tích chạy thi 100 m của 4 bạn An, Bình, Chi, Duy lần lượt là: 21,54 giây; $\frac{1}{3}$ phút; $\frac{{108}}{5}$ giây; $20\frac{3}{8}$ giây.

Hỏi bạn nào chạy nhanh nhất?

A

An
B

Bình
C

Chi
D

Duy

Đáp án : B

Phương pháp giải :

So sánh thành tích của các bạn: So sánh các số hữu tỉ

Bạn nào có thời gian chạy nhỏ nhất thì bạn đó chạy nhanh nhất.

Lời giải chi tiết :

Ta có: $\frac{1}{3}$ phút = $\frac{1}{3}$ . 60 = 20 giây

$\frac{{108}}{5}$ giây = 21,6 giây

$20\frac{3}{8}$ giây = 20,375 giây

Vì 20 < 20,375 < 21,54 < 21,6 nên Bình chạy nhanh nhất

Chú ý

+ Đưa các số liệu về cùng đơn vị rồi mới so sánh

+ Nếu các số hữu tỉ viết được dưới dạng số thập phân thì ta viết chúng ở dạng số thập phân rồi so sánh.

Câu 9 :

Cho số hữu tỉ $x = \frac{7}{{n + 2}}$

Tìm tổng của các số nguyên n sao cho x là một số nguyên

A

-4
B

4
C

0
D

-8

Đáp án : D

Phương pháp giải :

Để x là số nguyên thì $7 \vdots (n + 2)$ hay $(n + 2) \in$ Ư (7) = {1; -1; 7; -7}

Lời giải chi tiết :

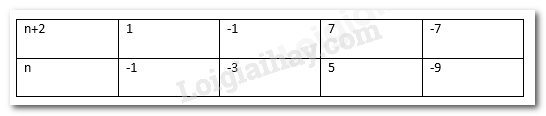
Để x là số nguyên thì $7 \vdots (n + 2)$ hay $(n + 2) \in$ Ư (7) = {1; -1; 7; -7}

Ta có bảng sau:

Vậy có 4 giá trị n thỏa mãn điều kiện.

Tổng của các giá trị n đó là: (-1) + (-3) + 5 + (-9) = -8

Câu 10 :

Số $\dfrac{9}{4}$ có số đối là:

A

$\dfrac{4}{9}$
B

$\dfrac{{ - 4}}{9}$
C

$\dfrac{9}{{ - 4}}$
D

$2,25$

Đáp án : C

Phương pháp giải :

2 số đối nhau là 2 số có tổng bằng 0.

Số đối của số hữu tỉ a là -a

Lời giải chi tiết :

Số đối của $\dfrac{9}{4}$ là $- \dfrac{9}{4} = \dfrac{9}{{ - 4}}$

Bài liên quan

Trắc nghiệm Bài 2: Các phép tính với số hữu tỉ Toán 7 Chân trời sáng tạo

Luyện tập và củng cố kiến thức Bài 2: Các phép tính với số hữu tỉ Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Trắc nghiệm Bài 3: Lũy thừa của một số hữu tỉ Toán 7 Chân trời sáng tạo

Luyện tập và củng cố kiến thức Bài 3: Lũy thừa của một số hữu tỉ Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Trắc nghiệm Bài 4: Quy tắc dấu ngoặc và quy tắc chuyển vế Toán 7 Chân trời sáng tạo

Luyện tập và củng cố kiến thức Bài 4: Quy tắc dấu ngoặc và quy tắc chuyển vế Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Trắc nghiệm Bài 1: Tập hợp các số hữu tỉ Toán 7 Chân trời sáng tạo

Trắc nghiệm Bài 2: Các phép tính với số hữu tỉ Toán 7 Chân trời sáng tạo

Trắc nghiệm Bài 3: Lũy thừa của một số hữu tỉ Toán 7 Chân trời sáng tạo

Trắc nghiệm Bài 4: Quy tắc dấu ngoặc và quy tắc chuyển vế Toán 7 Chân trời sáng tạo