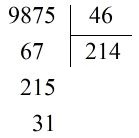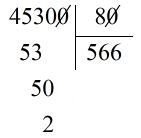Trắc nghiệm Bài 53: Em làm được những gì Toán 4 Chân trời sáng tạoĐề bài
Câu 1 :
Tìm phân số \(\dfrac{a}{b}\), biết phân số \(\dfrac{a}{b}\) là phân số tối giản sau khi rút gọn phân số \(\dfrac{{105}}{{135}}\). A. \(\dfrac{a}{b} = \dfrac{{13}}{{15}}\) B. \(\dfrac{a}{b} = \dfrac{{17}}{{27}}\) C. \(\dfrac{a}{b} = \dfrac{7}{9}\) D. \(\dfrac{a}{b} = \dfrac{5}{8}\)
Câu 2 :
Kết quả của phép chia \(9875:46\) là: A. \(214\) dư \(31\) B. \(213\) dư \(31\) C. \(213\) dư \(21\) D. \(214\) dư \(21\)
Câu 3 :
Số dư trong phép chia \(45300:80\) là A. \(2\) B. \(4\) C. \(20\) D. \(40\)
Câu 4 :
Nếu ${\rm{m = }}\,\,40,{\rm{ n}} = 4316$ thì biểu thức $\left( {10166 - 3846} \right):m+ n\,{\rm{ :}}\,52$ có giá trị là: A. \(241\) B. \(245\) C. \(235\) D. \(238\)
Câu 5 :
Điền số thích hợp vào ô trống: Có \(13\) xe nhỏ chở được \(11\) tấn \(2\) tạ hàng và \(27\) xe lớn chở được \(38\) tấn \(8\) tạ hàng. Vậy trung bình mỗi xe chở được ki-lô-gam hàng.
Câu 6 :
Tìm số bị chia và số chia bé nhất để phép chia đó có thương là \(249\) và số dư là \(96.\) A. Số bị chia: \(24240\); số chia: \(97\) B. Số bị chia: \(24240\); số chia: \(96\) C. Số bị chia: \(24249\); số chia: \(97\) D. Số bị chia: \(24000\); số chia: \(96\)
Câu 7 :
Tìm \(y\) , biết: $18 \times y + 27 \times y = 31048 - 20383$ A. $y = 233$ B. $y = 235$ C. $y = 237$ D. $y = 239$
Câu 8 :
Điền số thích hợp vào ô trống: Một kho chứa \(464\) bao xi măng, mỗi bao cân nặng \(50kg\). Người ta đã lấy đi \(\dfrac{1}{8}\) số xi măng đó. Vậy trong kho còn lại tạ xi măng.
Câu 9 :
Một mảnh vườn hình chữ nhật có chu vi là $112m$, chiều dài hơn chiều rộng \(16m\). Người ta trồng dâu tây trên mảnh vườn đó, cứ \(1{m^2}\) thu được $2kg$ dâu tây. Mỗi ki-lô-gam dâu tây bán với giá $75\,\,000$ đồng. Hỏi trên cả mảnh vườn đó thu được tất cả bao nhiêu tiền? A. \(108\,\,000\,\,000\) đồng B. \(118\,\,000\,\,000\) đồng C. \(248\,\,300\,\,000\) đồng D. \(460\,\,800\,\,000\) đồng
Câu 10 :
Trung bình cộng số tuổi của bố, Hoa và Huy là \(20\) tuổi. Tuổi bố hơn tổng số tuổi của Hoa và Huy là \(20\) tuổi, Hoa kém Huy \(4\) tuổi. Tính tuổi của mỗi người. A. Bố: \(39\) tuổi; Hoa: \(9\) tuổi; Huy: \(13\) tuổi B. Bố: \(40\) tuổi; Hoa: \(8\) tuổi; Huy: \(12\) tuổi C. Bố: \(42\) tuổi; Hoa: \(7\) tuổi; Huy: \(11\) tuổi D. Bố: \(44\) tuổi; Hoa: \(6\) tuổi; Huy: \(10\) tuổi Lời giải và đáp án
Câu 1 :
Tìm phân số \(\dfrac{a}{b}\), biết phân số \(\dfrac{a}{b}\) là phân số tối giản sau khi rút gọn phân số \(\dfrac{{105}}{{135}}\). A. \(\dfrac{a}{b} = \dfrac{{13}}{{15}}\) B. \(\dfrac{a}{b} = \dfrac{{17}}{{27}}\) C. \(\dfrac{a}{b} = \dfrac{7}{9}\) D. \(\dfrac{a}{b} = \dfrac{5}{8}\) Đáp án
C. \(\dfrac{a}{b} = \dfrac{7}{9}\) Phương pháp giải :
Khi rút gọn phân số có thể làm như sau: - Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn \(1\). - Chia tử số và mẫu số cho số đó. Cứ làm như thế cho đến khi nhận được phân số tối giản. Lời giải chi tiết :
Rút gọn phân số \(\dfrac{{105}}{{135}}\) ta có: \(\dfrac{{105}}{{135}} = \dfrac{{105:5}}{{135:5}} = \dfrac{{21}}{{27}} = \dfrac{{21:3}}{{27:3}} = \dfrac{7}{9}\) Ta thấy \(7\) và \(9\) không cùng chia hết cho số tự nhiên nào lớn hơn \(1\) nên \(\dfrac{7}{9}\) là phân số tối giản. Vậy \(\dfrac{a}{b} = \dfrac{7}{9}\).
Câu 2 :
Kết quả của phép chia \(9875:46\) là: A. \(214\) dư \(31\) B. \(213\) dư \(31\) C. \(213\) dư \(21\) D. \(214\) dư \(21\) Đáp án
A. \(214\) dư \(31\) Phương pháp giải :
Đặt tính rồi tính, chia theo thứ tự từ trái sang phải. Lời giải chi tiết :
Ta đặt tính và thực hiện tính như sau: Vậy: \(9875:46 = 214\) (dư \(31\)).
Câu 3 :
Số dư trong phép chia \(45300:80\) là A. \(2\) B. \(4\) C. \(20\) D. \(40\) Đáp án
C. \(20\) Phương pháp giải :
Đặt tính rồi tính, chia theo thứ tự từ trái sang phải. Từ đó xác định được số dư của phép chia đã cho. Lời giải chi tiết :
Ta đặt tính và thực hiện tính như sau: \(45300:80 = 566\) dư \(20\) Vậy số dư trong phép chia \(45300:80\) là \(20\).
Câu 4 :
Nếu ${\rm{m = }}\,\,40,{\rm{ n}} = 4316$ thì biểu thức $\left( {10166 - 3846} \right):m+ n\,{\rm{ :}}\,52$ có giá trị là: A. \(241\) B. \(245\) C. \(235\) D. \(238\) Đáp án
A. \(241\) Phương pháp giải :
- Thay ${\rm{m = }}\,\,40,{\rm{ n}} = 4316$ vào biểu thức $\left( {10166 - 3846} \right):m + n\,{\rm{ :}}\,52$ rồi tính giá trị biểu thức đó. - Biểu thức chứa dấu ngoặc thì ta tính trong ngoặc trước, ngoài ngoặc sau. - Biểu thức có chứa phép chia và phép cộng thì ta thực hiện phép tính chia trước, phép cộng sau. Lời giải chi tiết :
Nếu ${\rm{m = }}\,\,40,{\rm{ n}} = 4316$ thì: $\left( {10166 - 3846} \right):m+ n \,{\rm{ :}}\,52 $ $= \left( {10166 - 3846} \right):40+ 4316 \, {\rm{ :}}\,52 $ $= 6320:40 + 83 $ $= 158 + 83 = 241$ Vậy nếu ${\rm{m = }}\,40,{\rm{ n}} = 4316$ thì biểu thức $\left( {10166 - 3846} \right):m + n\,{\rm{ :}}\,52$ có giá trị là \(241\).
Câu 5 :
Điền số thích hợp vào ô trống: Có \(13\) xe nhỏ chở được \(11\) tấn \(2\) tạ hàng và \(27\) xe lớn chở được \(38\) tấn \(8\) tạ hàng. Vậy trung bình mỗi xe chở được ki-lô-gam hàng. Đáp án
Có \(13\) xe nhỏ chở được \(11\) tấn \(2\) tạ hàng và \(27\) xe lớn chở được \(38\) tấn \(8\) tạ hàng. Vậy trung bình mỗi xe chở được ki-lô-gam hàng. Phương pháp giải :
- Đổi tấn, tạ ra ki-lô-gam. Lưu ý: \(1\) tấn \(=1000kg;\, 1\) tạ \(=100kg\). - Tìm tổng số xe. - Tìm tổng số ki-lô-gam hàng chở được. - Tính trung bình số hàng mỗi xe chở được bằng cách lấy tổng số hàng chia cho tổng số xe. Lời giải chi tiết :
Đổi \(11\) tấn \(2\) tạ \( = \,11\) tấn \( + \,2\) tạ \( = \,11000kg + 200kg = 11200kg\) \(38\) tấn \(8\) tạ \( = \,38\) tấn \( + \,8\) tạ \( = \,38000kg + 800kg = 38800kg\) Có tất cả số xe là: \(13 + 27 = 40\) (xe) \(40\) xe được tất cả số ki-lô-gam hàng là: \(11200 + 38800 = 50000\,\,(kg)\) Trung bình mỗi xe chở số ki-lô-gam hàng là: \(50000:40 = 1250\,\,(kg)\) Đáp số: \(1250kg\). Vậy đáp án đúng điền vào ô trống là \(1250.\)
Câu 6 :
Tìm số bị chia và số chia bé nhất để phép chia đó có thương là \(249\) và số dư là \(96.\) A. Số bị chia: \(24240\); số chia: \(97\) B. Số bị chia: \(24240\); số chia: \(96\) C. Số bị chia: \(24249\); số chia: \(97\) D. Số bị chia: \(24000\); số chia: \(96\) Đáp án
C. Số bị chia: \(24249\); số chia: \(97\) Phương pháp giải :
- Tìm số chia: trong phép chia có dư, số chia bé nhất trong phép chia đó sẽ hơn số dư \(1\) đơn vị. - Tìm số bị chia dựa vào công thức: số bị chia = thương \( \times \) số chia + số dư. Lời giải chi tiết :
Vì số dư là \(96\) nên số chia bé nhất là: \(96 + 1 = 97\) Số bị chia là: \(249 \times 97 + 96 = 24249\) Vậy số bị chia là \(24249\); số chia là \(97\).
Câu 7 :
Tìm \(y\) , biết: $18 \times y + 27 \times y = 31048 - 20383$ A. $y = 233$ B. $y = 235$ C. $y = 237$ D. $y = 239$ Đáp án
C. $y = 237$ Phương pháp giải :
- Viết biểu thức bên trái dấu bằng về dạng một tổng nhân với một số. - Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết. Lời giải chi tiết :
$18 \times y + 27 \times y = 31048 - 20383\;$ $(18 + 27) \times y = 31048 - 20383\;$ $45 \times y = 10665$ $y = 10665:45$ $y = 237$ Vậy đáp án đúng là $y = 237$.
Câu 8 :
Điền số thích hợp vào ô trống: Một kho chứa \(464\) bao xi măng, mỗi bao cân nặng \(50kg\). Người ta đã lấy đi \(\dfrac{1}{8}\) số xi măng đó. Vậy trong kho còn lại tạ xi măng. Đáp án
Một kho chứa \(464\) bao xi măng, mỗi bao cân nặng \(50kg\). Người ta đã lấy đi \(\dfrac{1}{8}\) số xi măng đó. Vậy trong kho còn lại tạ xi măng. Phương pháp giải :
- Tìm khối lượng xi măng có trong kho lúc đầu ta lấy cân nặng của một bao nhân với số bao. - Tìm khối lượng xi măng đã lấy đi tức là ta tìm \(\dfrac{1}{8}\) của tổng khối lượng xi măng, hay ta lấy tổng khối lượng xi măng chia cho \(8\). - Tìm khối lượng xi măng còn lại ta lấy khối lượng xi măng có trong kho lúc đầu trừ đi khối lượng xi măng đã lấy đi. - Đổi số đo vừa tìm được sang đơn vị tạ. Lời giải chi tiết :
Kho đó có tất cả số ki-lô-gam xi măng là: \(50 \times 464 = 23200\,\,(kg)\) Người ta đã lấy đi số ki-lô-gam xi măng là: \(23200:8 = 2900\,\,(kg)\) Trong kho còn lại số ki-lô-gam xi măng là: \(23200 - 2900 = 20300\,\,(kg)\) \(20300kg = 203\) tạ Đáp số: \(203\) tạ. Vậy đáp án đúng điền vào ô trống là \(203\).
Câu 9 :
Một mảnh vườn hình chữ nhật có chu vi là $112m$, chiều dài hơn chiều rộng \(16m\). Người ta trồng dâu tây trên mảnh vườn đó, cứ \(1{m^2}\) thu được $2kg$ dâu tây. Mỗi ki-lô-gam dâu tây bán với giá $75\,\,000$ đồng. Hỏi trên cả mảnh vườn đó thu được tất cả bao nhiêu tiền? A. \(108\,\,000\,\,000\) đồng B. \(118\,\,000\,\,000\) đồng C. \(248\,\,300\,\,000\) đồng D. \(460\,\,800\,\,000\) đồng Đáp án
A. \(108\,\,000\,\,000\) đồng Phương pháp giải :
- Tính nửa chu vi: Nửa chu vi \(=\) chu vi \(:\,2= \) chiều dài \(+\) chiều rộng. - Tìm chiều dài và chiều rộng dựa vào công thức tìm hai số khi biết tổng và hiệu của hai số : Số bé = (tổng – hiệu) : $2$; Số lớn = (tổng + hiệu) : $2$. - Tính diện tích = chiều dài × chiều rộng. - Tính khối lượng dâu tây thu được ta lấy số dâu tây thu hoạch được trên \(1{m^2}\) nhân với diện tích mảnh vườn. - Tính số tiền thu được ta lấy giá bán của \(1kg\) nhân với khối lượng dâu tây thu được. Lời giải chi tiết :
Nửa chu vi mảnh vườn là: $112:2 = 56\,\,(m)$ Chiều rộng của mảnh vườn hình chữ nhật đó là: \((56 - 16):2 = 20\,(m)\) Chiều dài của mảnh vườn hình chữ nhật đó là: \(20 + 16 = 36\,\,(m)\) Diện tích của mảnh vườn hình chữ nhật đó là: \(36\, \times 20 = 720\,\,({m^2})\) Trên cả mảnh vườn đó người ta thu được số ki-lô-gam dâu tây là: \(720 \times 2 = 1440\,(kg)\) Trên cả mảnh vườn đó người ta thu được số tiền là \(75\,\,000 \times 1440 = \,\,\,108\,\,000\,\,000\) (đồng) Đáp số: \(108\,\,000\,\,000\) đồng.
Câu 10 :
Trung bình cộng số tuổi của bố, Hoa và Huy là \(20\) tuổi. Tuổi bố hơn tổng số tuổi của Hoa và Huy là \(20\) tuổi, Hoa kém Huy \(4\) tuổi. Tính tuổi của mỗi người. A. Bố: \(39\) tuổi; Hoa: \(9\) tuổi; Huy: \(13\) tuổi B. Bố: \(40\) tuổi; Hoa: \(8\) tuổi; Huy: \(12\) tuổi C. Bố: \(42\) tuổi; Hoa: \(7\) tuổi; Huy: \(11\) tuổi D. Bố: \(44\) tuổi; Hoa: \(6\) tuổi; Huy: \(10\) tuổi Đáp án
B. Bố: \(40\) tuổi; Hoa: \(8\) tuổi; Huy: \(12\) tuổi Phương pháp giải :
- Tính tổng số tuổi của ba người ta lấy số tuổi trung bình nhân với \(3\). - Coi tuổi bố là số lớn, tổng số tuổi của Hoa và Huy là số bé. Ta tìm số lớn và số bé theo công thức tìm hai số khi biết tổng và hiệu : Số bé = (tổng – hiệu) : $2$; Số lớn = (tổng + hiệu) : $2$. - Tìm được tổng số tuổi của Hoa và Huy, lại có hiệu số tuổi của 2 người, áp dụng công thức tìm hai số khi biết tổng và hiệu ta tìm được tuổi của mỗi người. Lời giải chi tiết :
Tổng số tuổi của ba người là: \(20 \times 3 = 60\) (tuổi) Tuổi bố là: \((60 + 20):2 = 40\) (tuổi) Tổng số tuổi của Hoa và Huy là: \(60 - 40 = 20\) (tuổi) Tuổi Hoa là: \((20 + 4):2 = 12\) (tuổi) Tuổi Huy là: \(20 - 12 = 8\) (tuổi) Đáp số: Bố: \(40\) tuổi; Hoa: \(8\) tuổi; Huy: \(12\) tuổi.
|
