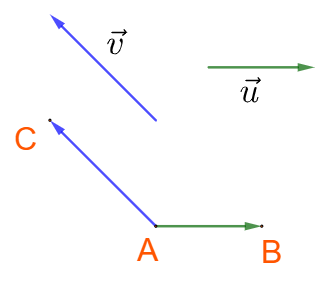
Lý thuyết Tích vô hướng của hai vecto - SGK Toán 10 CTST1. GÓC GIỮA HAI VECTO Tổng hợp đề thi học kì 2 lớp 10 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa... 1. GÓC GIỮA HAI VECTO Cho hai vecto →u và →v khác →0. Góc giữa hai vecto →u và →v , kí hiệu (→u,→v) a) Cách xác định góc: Chọn điểm A bất kì, vẽ →AB=→u và →AC=→v. Khi đó (→u,→v)=^BAC.
b) Các trường hợp đặc biệt: +) (→u,→0)=α tùy ý, với 0∘≤α≤180∘ +) (→u,→v)=90∘⇔→u⊥→v hoặc →v⊥→u. Đặc biệt: →0⊥→u∀→u +) (→u,→v)=0∘⇔→u,→v cùng hướng +) (→u,→v)=180∘⇔→u,→v ngược hướng
2. TÍCH VÔ HƯỚNG CỦA HAI VECTO +) Tích vô hướng của hai vecto →u,→v: →u.→v=|→u|.|→v|.cos(→u,→v) +) →u.→v=0⇔→u⊥→v +) →u.→u=→u2=|→u|.|→u|.cos0∘=|→u|2
3. TÍNH CHẤT CỦA TÍCH VÔ HƯỚNG Cho 3 vecto →u,→v,→w bất kì và mọi số thực k, ta có: →u.→v=→v.→u→u.(→v+→w)=→u.→v+→u.→w(k→u).→v=k.(→u.→v)=→u.(k→v) Hệ quả →u.(→v−→w)=→u.→v−→u.→w(→u+→v)2=→u2+2→u.→v+→v2;(→u−→v)2=→u2−2→u.→v+→v2(→u+→v)(→u−→v)=→u2−→v2 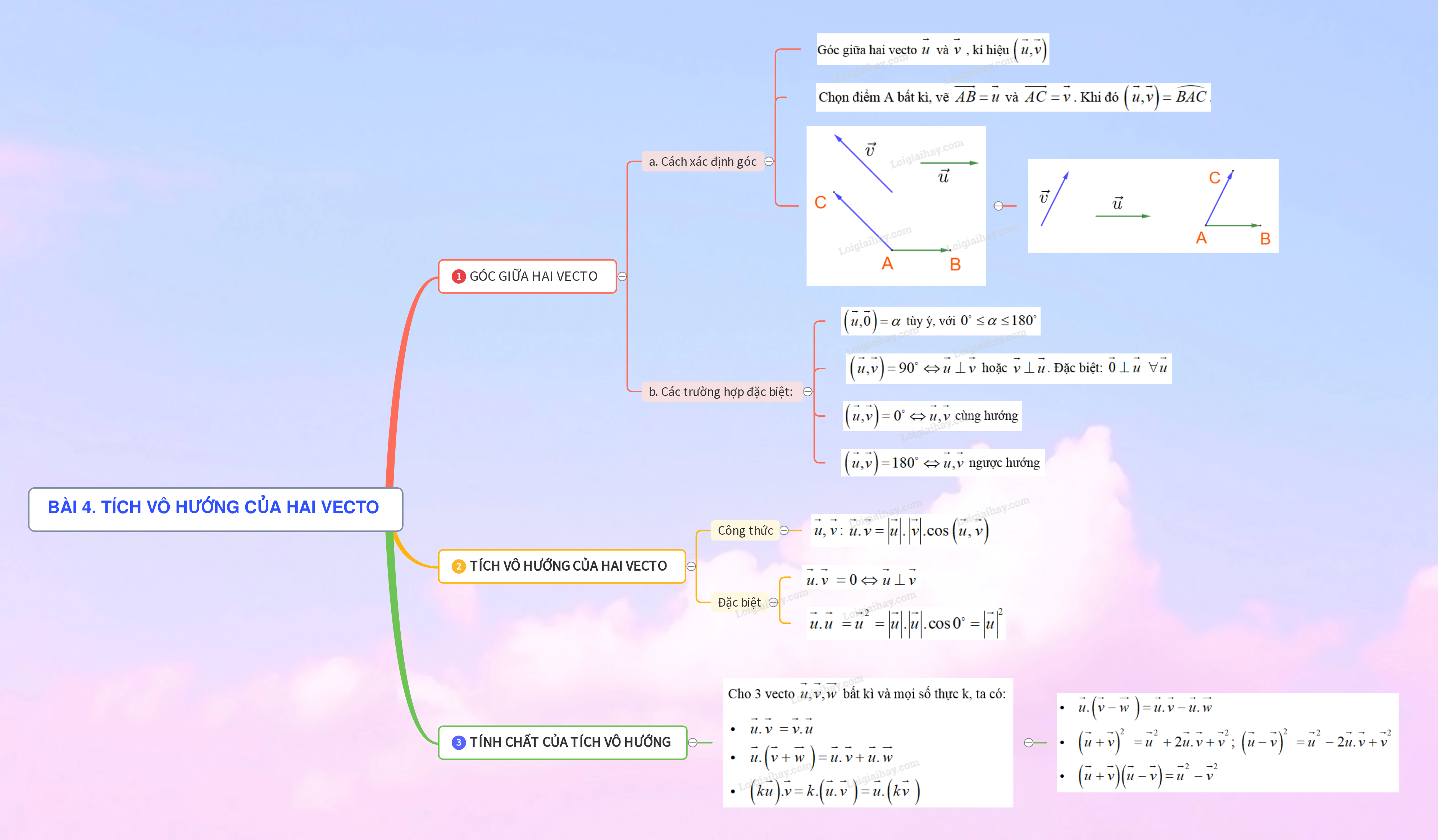
|