Giải mục 2 trang 99, 100 SGK Toán 10 tập 1 - Chân trời sáng tạoMột người dùng một lực F có cường độ là 10 N kéo một chiếc xe đi quãng đường dài 100 m. Cho tam giác ABC vuông cân tại A, có cạnh huyền bằng Một người dùng một lực F có độ lớn là 20 N kéo một vật dịch chuyển một đoạn 50 m Tổng hợp đề thi học kì 2 lớp 10 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...
Lựa chọn câu để xem lời giải nhanh hơn
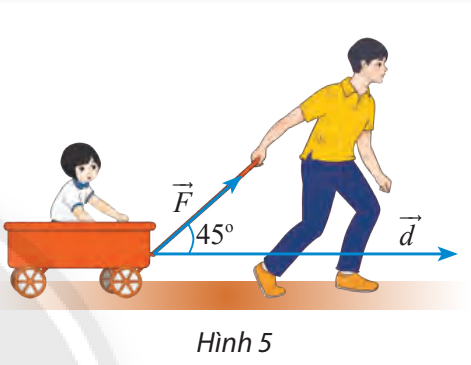
HĐ Khám phá 2 Một người dùng một lực →F có cường độ là 10 N kéo một chiếc xe đi quãng đường dài 100 m. Tính công sinh bởi lực →F, biết rằng góc giữa vectơ →F và hướng di chuyển là 45∘. (Công A (đơn vị: J) bằng tích của ba đại lượng: cường độ của lực →F, độ dài quãng đường và côsin các góc giữa vectơ →F và độ dịch chuyển →d).
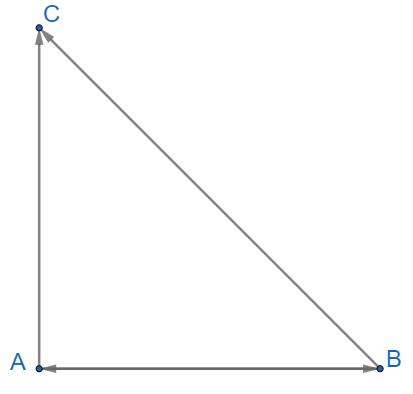
Lời giải chi tiết: Theo giả thiết ta có: A=|→F|.|→d|.cos(→F,→d) ⇒A=10.100.cos45∘=500√2(J) Vậy công sinh bởi lực →F là 500√2 (J) Thực hành 2 Cho tam giác ABC vuông cân tại A, có cạnh huyền bằng √2. Tính các tích vô hướng: →AB.→AC,→AC.→BC,→BA.→BC Phương pháp giải: Bước 1: Vận dụng công thức →AB.→AC=|→AB|.|→AC|.cos(→AB,→AC) Bước 2: Xác định độ dài cạnh AB, AC và góc giữa hai vecto (→AB,→AC)=^BAC Lời giải chi tiết:
+) Ta có: AB⊥AC⇒→AB⊥→AC⇒→AB.→AC=0 +) →AC.→BC=|→AC|.|¯BC|.cos(→AC,→BC) Ta có: BC=√AB2+AC2=√2⇔√2AC2=√2⇒AC=1 ⇒→AC.→BC=1.√2.cos(45∘)=1 +) →BA.→BC=|→BA|.|→BC|.cos(→BA,→BC)=1.√2.cos(45∘)=1 Thực hành 3 Hai vectơ →a và →b có độ dài lần lượt là 3 và 8 có tích vô hướng là 12√2.Tính góc giữa hai vectơ →a và →b Phương pháp giải: Sử dụng công thức →a.→b=|→a|.|→b|.cos(→a,→b)⇒cos(→a,→b)=→a.→b|→a|.|→b| Lời giải chi tiết: Ta có: →a.→b=|→a|.|→b|.cos(→a,→b) ⇔12√2=3.8.cos(→a,→b)⇔cos(→a,→b)=√22 ⇒(→a,→b)=45∘ Vậy góc giữa hai vectơ →a và →b là 45∘ Vận dụng 1 Một người dùng một lực →F có độ lớn là 20 N kéo một vật dịch chuyển một đoạn 50 m cùng hướng với →F. Tính công sinh bởi lực →F. Phương pháp giải: Công thức tính công: A=→F.→d Tích vô hướng: →F.→d=|→F|.|→d|.cos(→F,→d) Lời giải chi tiết: Gọi vectơ dịch chuyển của vật là →d, ta có |→d|=50. Theo giả thiết →F và →d cùng hướng nên (→F,→d)=0∘ Công sinh ra bởi lực →Fđược tính bằng: A=→F.→d=|→F|.|→d|.cos(→F,→d)=20.50.cos0∘=1000 (J)
|