Lý thuyết Nguyên hàm Toán 12 Cùng khám phá1. Khái niệm nguyên hàm 1. Khái niệm nguyên hàm
Chú ý: Giả sử hàm số F(x) là một nguyên hàm của f(x) trên K. Khi đó: a) Với mỗi hằng số C, hàm số F(x) + C cũng là một nguyên hàm của f(x) trên K. b) Nếu hàm số G(x) là một nguyên hàm của f(x) trên K thì tồn tại một hằng số C sao chp G(x) = F(x) + C với mọi x thuộc K. Như vậy, nếu F(x) là một nguyên hàm của f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C (C là hằng số). Ta gọi F(x) + với C thuộc R là họ các nguyên hàm của f(x) trên K, kí hiệu ∫f(x)dx=F(x)+C. Ví dụ: Chứng minh ∫kdx=kx+C với k là hằng số khác 0. Giải: Ta có (kx)′=k nên F(x)=kx là một nguyên hàm của hàm số f(x)=k. Vậy ∫kdx=kx+C. Nhận xét: Ta có ∫0dx=C, ∫dx=∫1dx=x+C. 2. Nguyên hàm của một số hàm số thường gặp Nguyên hàm của hàm số lũy thừa
Ví dụ: a) ∫x5dx=16x6+C. b) ∫x√2dx=1√2+1x√2+1+C. c) ∫x−1dx=∫1xdx=ln|x|+C. Nguyên hàm của hàm số mũ
Ví dụ: a) ∫4xdx=4xln4+C. b) ∫e3xdx=∫(e3)xdx=(e3)xlne3+C=13e3x+C. c) ∫2x.3xdx=∫6xdx=6xln6+C. Nguyên hàm của hàm số lượng giác
Ví dụ: a) ∫(1+tan2x)dx=∫1cos2xdx=tanx+C. b) Tìm nguyên hàm F(x) của hàm số f(x) = sinx, biết F(2π)=0. Ta có ∫sinxdx=−cosx+C. F(x) là nguyên hàm của hàm số f(x) = sinx nên có dạng F(x) = -cosx + C. Vì F(2π)=0 nên −cos2π+C=0 hay −1+C=0, suy ra C = 1. Vậy F(x) = 1 – cosx. 3. Tính chất cơ bản của nguyên hàm
Ví dụ: a) ∫6x3dx=6∫x3dx=6.x44+C=32x4+C. b) ∫(3x2−cosx)dx=3∫x2dx−∫cosxdx=x3−sinx+C. c) ∫(2cos2x−5x)dx=2∫1cos2xdx−∫5xdx=2tanx−5xln5+C. 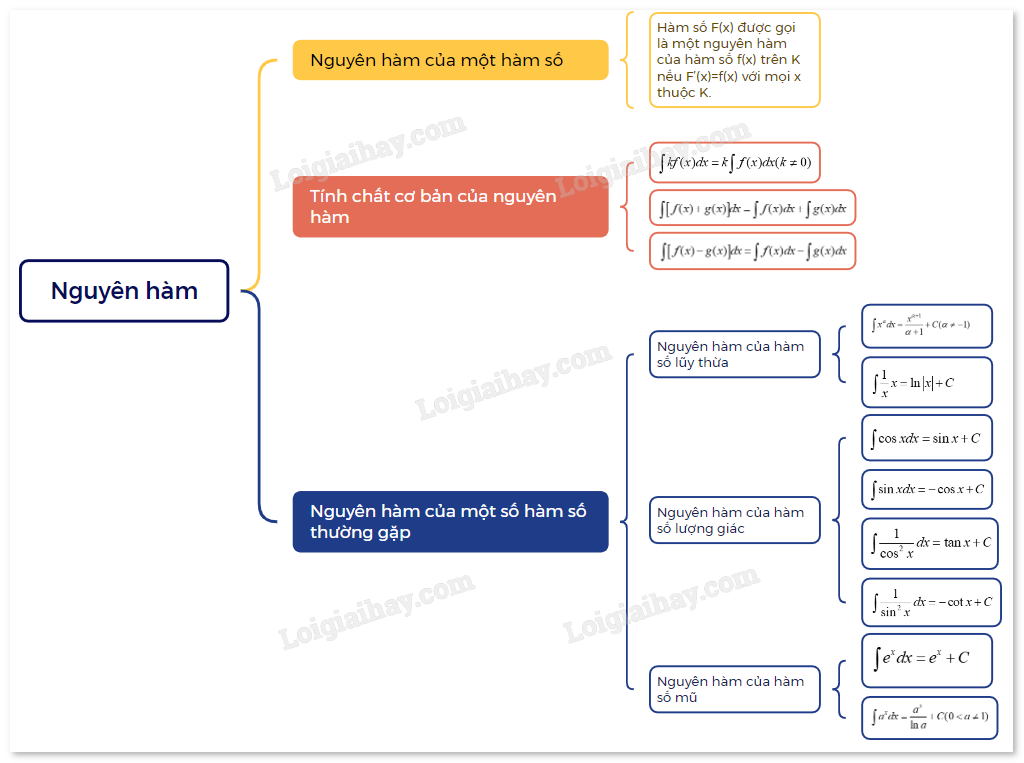
>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD - Click xem ngay) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
|





















