Lý thuyết Một số hệ thức về cạnh và góc trong tam giác vuông Toán 9 Cùng khám phá1. Một số hệ thức về cạnh và góc trong tam giác vuông Trong tam giác vuông, mỗi cạnh góc vuông bằng: + cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề. Cạnh góc vuông = (cạnh huyền ) × (sin góc đối) = (cạnh huyền ) × (cosin góc kề) + cạnh góc vuông kia nhân với tang góc đối hoặc côtang góc kề. Cạnh góc vuông = (cạnh góc vuông còn lại ) × (tan góc đối) = (cạnh góc vuông còn lại ) × (cot góc kề) Tổng hợp Đề thi vào 10 có đáp án và lời giải Toán - Văn - Anh 1. Một số hệ thức về cạnh và góc trong tam giác vuông
Ví dụ:
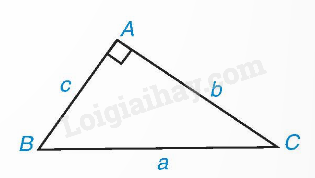
Trong tam giác ABC vuông tại A, ta có: \(\begin{array}{l}b = a.\sin B = a.\cos C;\\c = a.\sin C = a.\cos B.\end{array}\) \(\begin{array}{l}b = c.\tan B = c.\cot C;\\c = b.\tan C = b.\cot B.\end{array}\) 2. Giải tam giác vuông Bài toán Giải tam giác vuông Bài toán xác định số đo tất cả các góc và độ dài tất cả các cạnh của một tam giác vuông được gọi là bài toán giải tam giác vuông. Ta có thể giải được một tam giác vuông nếu biết độ dài của hai cạnh bất kì hoặc độ dài một cạnh cùng với số đo một góc nhọn bất kì của nó. 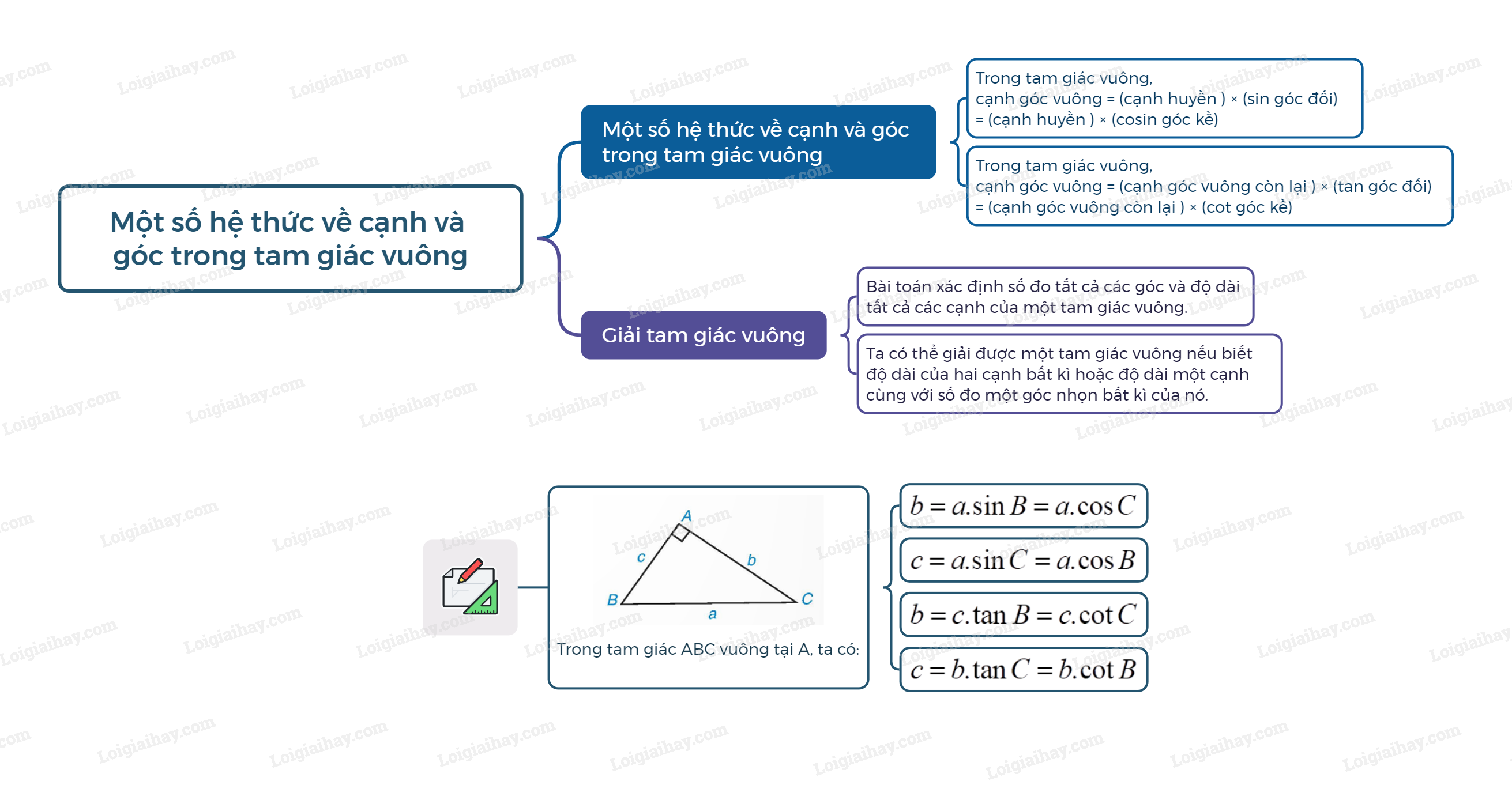
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
|