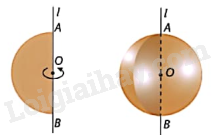
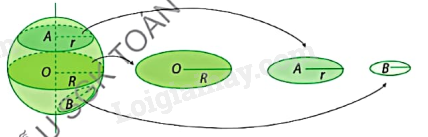
Lý thuyết Hình cầu Toán 9 Cùng khám phá1. Hình cầu Khi cắt hình cầu bởi một mặt phẳng, ta được một hình tròn. Khi cắt mặt cầu bởi một hình phẳng, ta được một hình tròn. Nếu mặt phẳng đi qua tâm của mặt cầu thì đường tròn đó có bán kính R và được gọi là đường tròn lớn. Nếu mặt phẳng không đi qua tâm của mặt cầu thì đường tròn đó có bán kính bé hơn R. 1. Hình cầu
Ví dụ: Khi cắt hình cầu bởi các mặt phẳng khác nhau, ta được các hình tròn có bán kính khác nhau. 2. Diện tích của mặt cầu
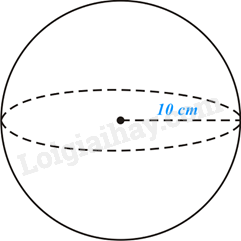
Ví dụ:
Diện tích mặt cầu là: S=4πR2=4π.102=400π(cm2), 3. Thể tích hình cầu
Ví dụ:
Thể tích hình cầu là: V=43πR3=43π.103=4000π3(cm3). 
|