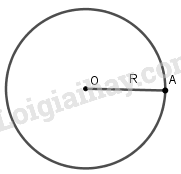
Lý thuyết Đường tròn Toán 9 Chân trời sáng tạo1. Khái niệm đường tròn Đường tròn tâm O bán kính R (R > 0), là hình gồm tất cả các điểm cách điểm O một khoảng bằng R, kí hiệu (O; R). Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - KHTN - Lịch sử và Địa lí 1. Khái niệm đường tròn
Khi không cần chú ý đến bán kính, đường tròn (O;R) còn được kí hiệu là (O). Vị trí tương đối của điểm và đường tròn
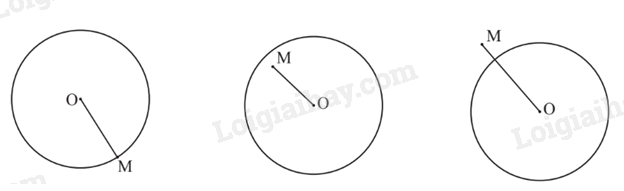
Cho đường tròn (O; R) và điểm M. Khi đó: - Nếu OM = R thì điểm M nằm trên đường tròn hay M thuộc đường tròn; - Nếu OM < R thì điểm M nằm trong đường tròn; - Nếu OM > R thì điểm M nằm ngoài đường tròn. 2. Tính đối xứng của đường tròn
Ví dụ:
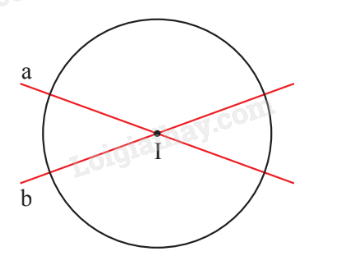
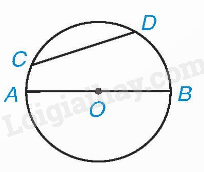
Hình tròn tâm I có: I là tâm đối xứng; Đường thẳng a, b là các trục đối xứng của hình tròn (I). 3. Đường kính và dây cung của đường tròn Cho hai điểm C, D cùng thuộc một đường tròn. Đoạn thẳng CD gọi là dây cung hoặc dây. Đường kính AB là một dây đi qua tâm.
Quan hệ giữa dây và đường kính
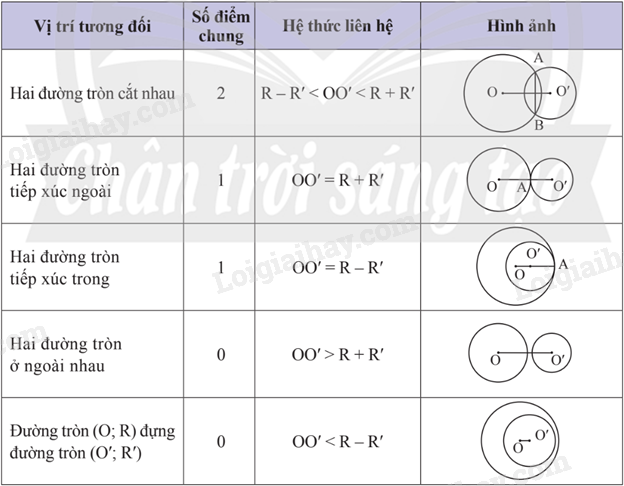
4. Vị trí tương đối của hai đường tròn
Chú ý: Nếu OO’ = 0 thì O trùng với O’. Hai đường tròn có tâm trùng nhau gọi là hai đường tròn đồng tâm. Bảng tóm tắt vị trí tương đối của hai đường tròn phân biệt (O;R) và (O’; R’) với R≥R′
Ví dụ 1: Cho OO’ = 5cm, khi đó hai đường tròn (O;4cm) và (O’;3cm) cắt nhau vì: 4cm – 3cm = 1cm < 5cm < 7cm = 4cm + 3cm. Ví dụ 2: Cho OO’ = 5cm, khi đó hai đường tròn (O;3cm) và (O’;2cm) tiếp xúc ngoài với nhau vì 5cm = 3cm + 2cm. Cho OO’ = 3cm, khi đó hai đường tròn (O;8cm) và (O’;5cm) tiếp xúc trong với nhau vì 3cm = 8cm - 5cm. Ví dụ 3: Cho đường tròn (O;3cm) và (O’;4cm) có OO′>8cm thì OO′=8cm>3cm+4cm=R+R′ nên (O;3cm) và (O’;4cm) là hai đường tròn ngoài nhau. 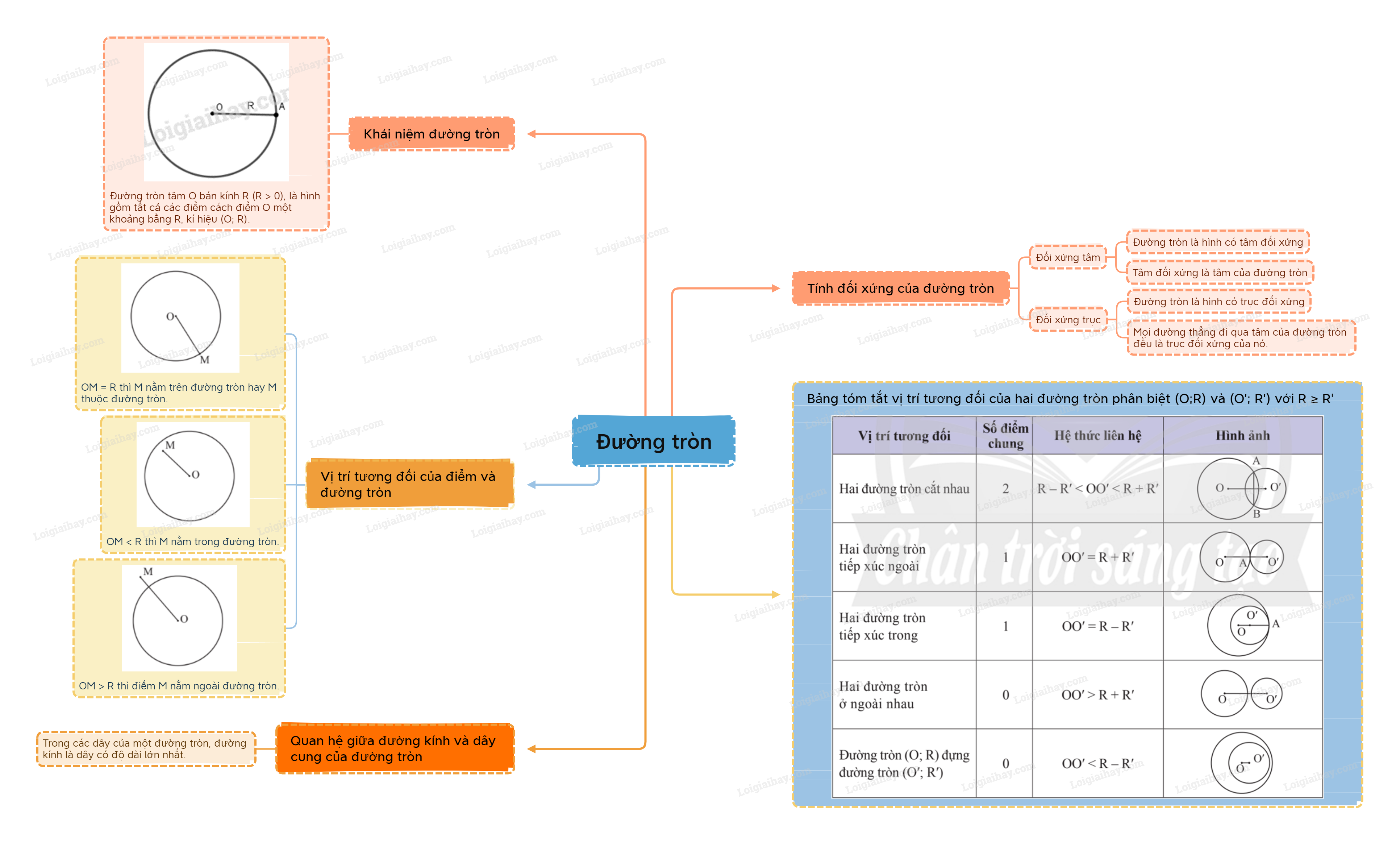
>> Học trực tuyến Lớp 9 & Lộ trình UP10 trên Tuyensinh247.com >> Chi tiết khoá học xem: TẠI ĐÂY Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
|