Lý thuyết Căn bậc hai Toán 9 Chân trời sáng tạo1. Căn bậc hai Khái niệm căn bậc hai Cho số thực a không âm. Số thực x thỏa mãn \({x^2} = a\) được gọi là một căn bậc hai của a. Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - KHTN - Lịch sử và Địa lí 1. Căn bậc hai Khái niệm căn bậc hai
Chú ý: - Mỗi số dương a có đúng hai căn bậc hai là hai số đối nhau: số dương là \(\sqrt a \) (căn bậc hai số học của a) và số âm là \( - \sqrt a \). - Số 0 chỉ có đúng một căn bậc hai là chính nó, ta viết \(\sqrt 0 = 0\). - Số âm không có căn bậc hai. - Phép toán tìm căn bậc hai số học của số không âm gọi là phép khai căn bậc hai hay phép khai phương (gọi tắt là khai phương). - Nếu \(a > b > 0\) thì \(\sqrt a > \sqrt b \). Suy ra \( - \sqrt a < - \sqrt b < 0 < \sqrt b < \sqrt a \). Ví dụ:
2. Tính căn bậc hai của một số bằng máy tính cầm tay
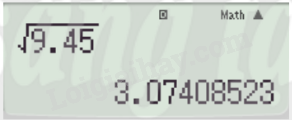
Ví dụ: Bấm lần lượt các phím
Vậy căn bậc hai của 9,45 (làm tròn đến chữ số thập phân thứ hai) là 3,07 và -3,07. Tính chất của căn bậc hai
Ví dụ: \(\sqrt {{{\left( {1 + \sqrt 2 } \right)}^2}} = \left| {1 + \sqrt 2 } \right| = 1 + \sqrt 2 \); \(\sqrt {{{\left( { - 3} \right)}^2}} = \left| { - 3} \right| = 3\). 3. Căn thức bậc hai Khái niệm căn thức bậc hai
Ví dụ: \(\sqrt {2x - 1} \), \(\sqrt { - \frac{1}{3}x + 2} \) là các căn thức bậc hai. Chú ý: - Ta cũng nói \(\sqrt A \) là một biểu thức. Biểu thức \(\sqrt A \) xác định (hay có nghĩa) khi A nhận giá trị không âm. - Khi A nhận giá trị không âm nào đó, khai phương giá trị này ta nhận được giá trị tương ứng của biểu thức \(\sqrt A \). Ví dụ: + Căn thức \(\sqrt {2x + 1} \) xác định khi \(2x + 1 \ge 0\) hay \(x \ge - \frac{1}{2}\). Tại \(x = 4\) thì \(\sqrt {2.4 + 1} = \sqrt 9 = \sqrt {{3^2}} = 3\). + Giá trị của biểu thức \(\sqrt {{b^2} - 4ac} \) tại \(a = 3;b = 10;c = 3\) là: \(\sqrt {{{10}^2} - 4.3.3} = \sqrt {100 - 36} = \sqrt {64} = \sqrt {{8^2}} = 8\). 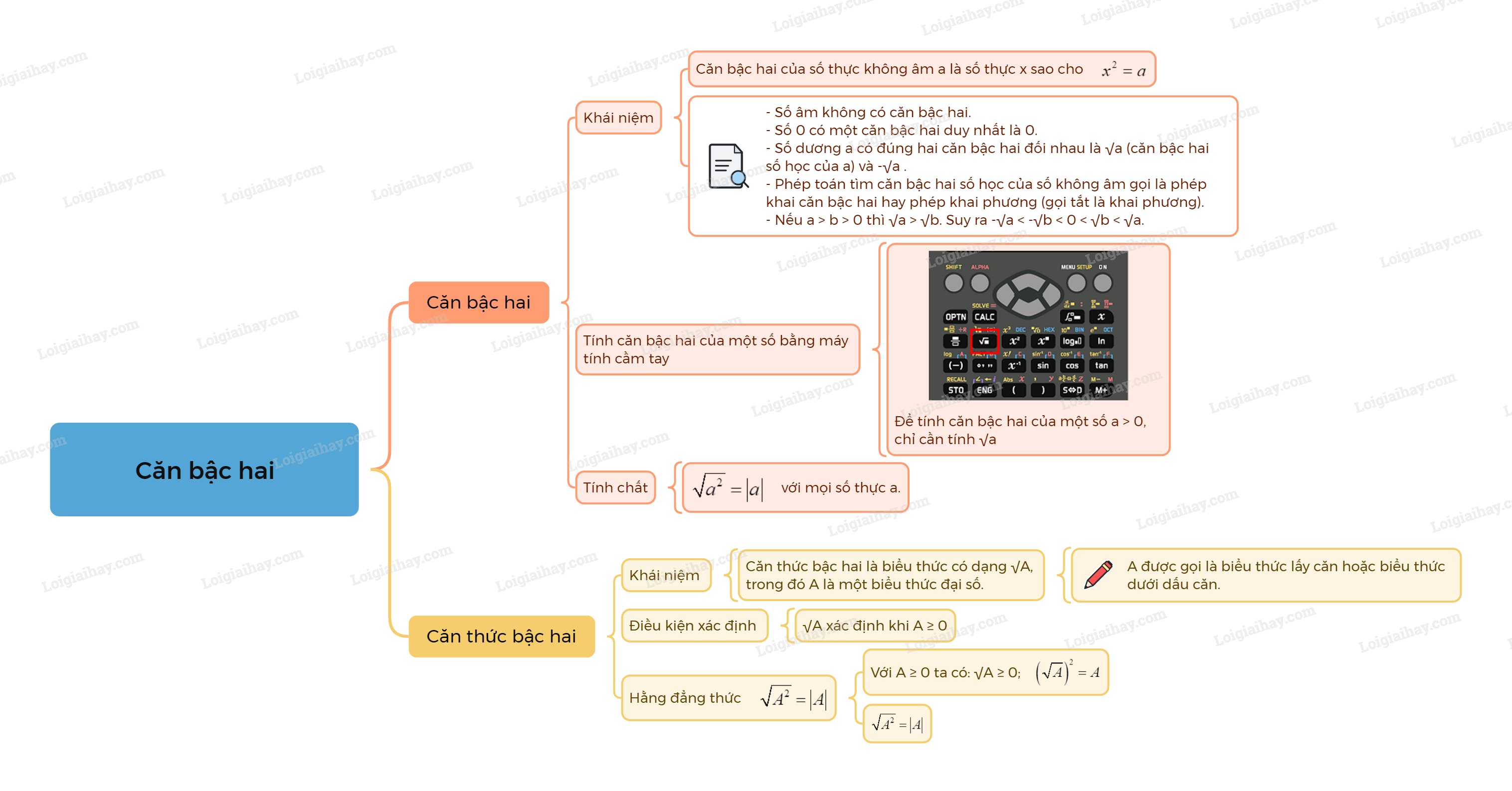
|













 ta tính được \(\sqrt {9,45} \approx 3,07\).
ta tính được \(\sqrt {9,45} \approx 3,07\).