Lý thuyết Cách tính xác suất của biến cố trong một số mô hình đơn giản Toán 9 Cùng khám phá1. Kết quả thuận lợi cho một biến cố Cho A là một biến cố liên quan đến phép thử ngẫu nhiên T. Một kết quả của T dẫn đến việc xảy ra biến cố A được gọi là kết quả thuận lợi cho biến cố A. Tổng hợp Đề thi vào 10 có đáp án và lời giải Toán - Văn - Anh 1. Kết quả thuận lợi cho một biến cố
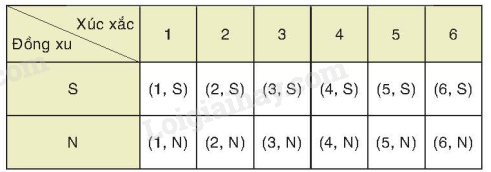
Ví dụ: Bạn Lan gieo một con xúc xắc và bạn Hòa gieo một đồng xu được gọi là phép thử. Kết quả của phép thử là số chấm xuất hiện trên con xúc xác và mặt xuất hiện của đồng xu. Các kết quả có thể của phép thử là:
Các kết quả thuận lợi cho biến cố “Số chấm xuất hiện trên con xúc xắc là số chẵn và mặt xuất hiện của đồng xu là mặt sấp” là (2, S); (4, S); (6, S). 2. Tính xác suất của biến cố
Cách tính xác suất của một biến cố
Ví dụ: Ba bạn Bảo, Châu, Dương được xếp ngẫu nhiên ngồi trên một hàng ghế có ba chỗ ngồi. Tính xác suất của các biến cố sau: a) E: "Bảo không ngồi ngoài cùng bên phải"; b) F: “Châu và Dương không ngồi cạnh nhau”. Lời giải: Kí hiệu ba bạn Bảo, Châu, Dương lần lượt là B, C, D. Vì việc xếp chỗ ngồi là ngẫu nhiên nên các kết quả có thể là đồng khả năng. Ta liệt kê các kết quả có thể xảy ra: • Bảo ngồi ngoài cùng bên trái: có 2 cách xếp là BCD và BDC. • Bảo ngồi giữa: có 2 cách xếp là CBD và DBC. • Bảo ngồi ngoài cùng bên phải: có 2 cách xếp là CDB và DCB. Vậy không gian mẫu của phép thử là \(\Omega = \left\{ {BCD;{\rm{ }}BDC;{\rm{ }}CBD;{\rm{ }}DBC;{\rm{ }}CDB;{\rm{ }}DCB} \right\}.\) Tập \(\Omega \) có 6 phần tử. a) Có 4 kết quả thuận lợi cho biến cố E là BCD, BDC, CBD và DBC. Vậy \(P\left( E \right) = \frac{4}{6} = \frac{2}{3}\). b) Có 2 kết quả thuận lợi cho biến cố F là CBD và DBC. Vậy \(P\left( F \right) = \frac{2}{6} = \frac{1}{3}\). 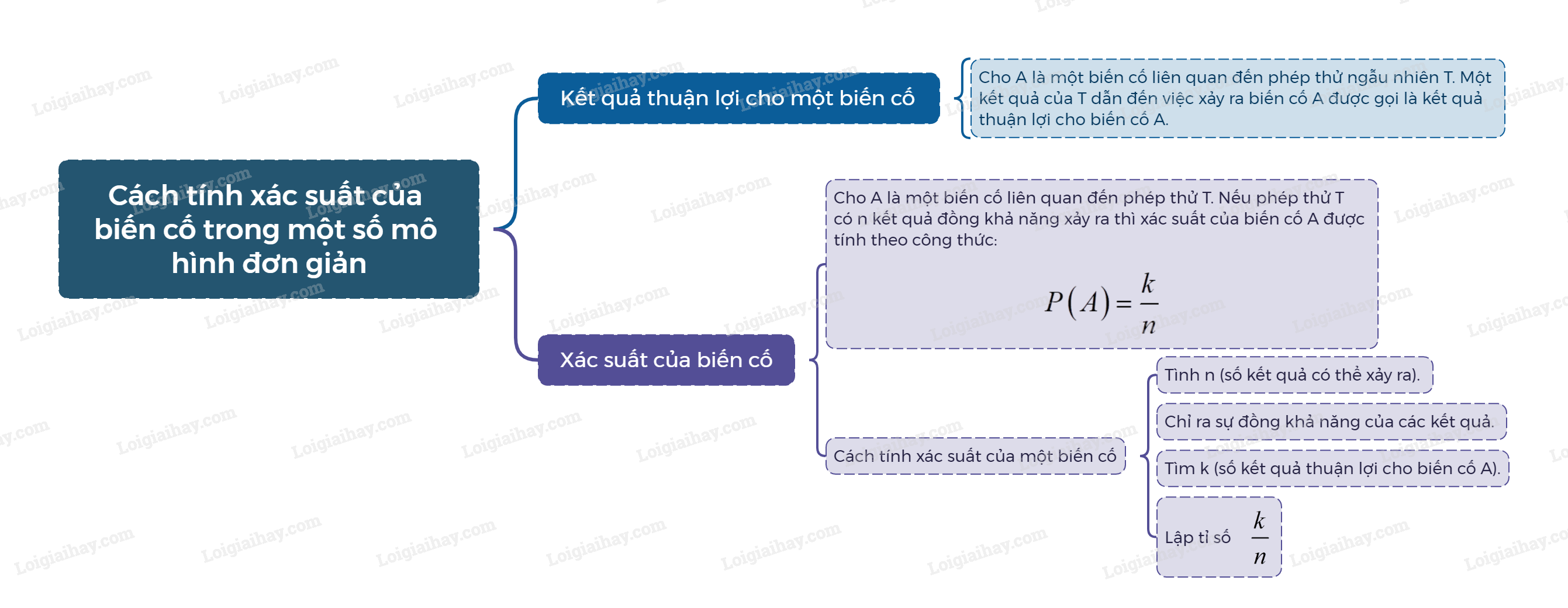
>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
|