Bài 2. Thực hành về mô phỏng trang 161 SGK Tin học 12 Cánh diềuCho góc vuông xOy với điểm O cố định, Tổng hợp đề thi học kì 2 lớp 12 tất cả các môn - Cánh diều Toán - Văn - Anh - Hoá - Sinh - Sử - Địa
Lựa chọn câu để xem lời giải nhanh hơn
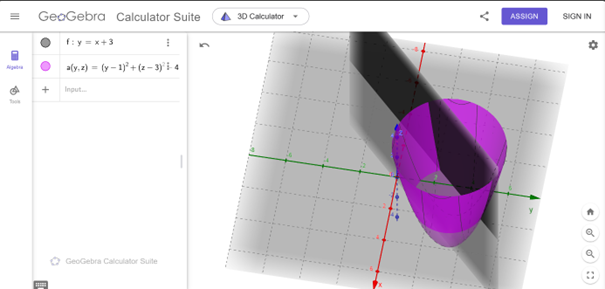
CH tr 161 VD1 Cho góc vuông xOy với điểm O cố định, điểm A cố định trên Oy, khi điểm B di chuyển trên Ox thì điểm M là trung điểm của AB di chuyển ra sao. Phương pháp giải: Sử dụng phần mềm Geogebra để giải quyết bài toán. Sử dụng hệ tọa độ để giải. Lời giải chi tiết: Khi điểm B di chuyển trên trục Ox, điểm M sẽ là trung điểm của đoạn thẳng AB. Để mô tả di chuyển của điểm M, chúng ta có thể sử dụng hệ tọa độ. Gọi tọa độ của điểm A là (0;yA) là tọa độ của điểm A trên trục Oy. Gọi tọa độ của điểm B là (xB;0) là tọa độ của điểm B trên trục Ox. Do M là trung điểm của AB, ta có: Tọa độ của điểm M là Khi B di chuyển trên trục Ox, tọa độ của điểm B thay đổi, do đó tọa độ của M cũng thay đổi tương ứng theo công thức trên. Tóm lại, khi B di chuyển trên trục Ox, M di chuyển sao cho tọa độ của M thay đổi theo công thức , tức là tọa độ y của M không thay đổi, và tọa độ x của M luôn là . 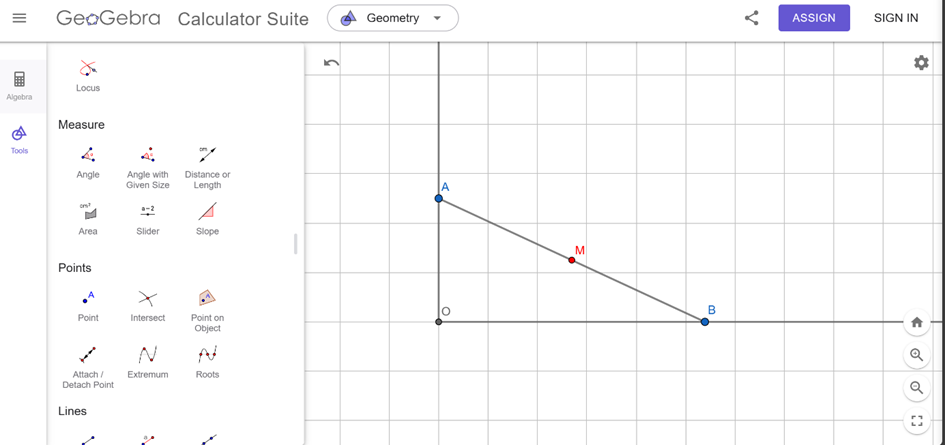 CH tr 161 VD2 Hãy hiển thị mặt phẳng y = x + 3 và mặt trụ (y - 1)² + (z-3)² = 4. Phần giao giữa hai mặt này là hình gì? Phương pháp giải: Sử dụng phần mềm Geogebra để mô phỏng 2 mặt phẳng. Hình giao nhau sẽ là một đường cong trong không gian. Lời giải chi tiết: Khi hai hình này giao nhau, hình giao sẽ là một đường cong trong không gian. Cụ thể, nếu ta xem xét phần giao giữa mặt phẳng và mặt trụ, điều này sẽ là một đường cong trên mặt phẳng yz với một độ dốc nhất định.
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
|