Bài 12. Điện trường trang 43, 44, 45, 46, 47 SBT Vật lí 11 Chân trời sáng tạoĐơn vị của cường độ điện trường là Tổng hợp đề thi học kì 2 lớp 11 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh
Lựa chọn câu để xem lời giải nhanh hơn
Trắc nghiệm 12.1 Đề bài: Đơn vị của cường độ điện trường là A. V/m, C/N. B. V.m, N.C. C. V/m, N/C. D. V.m, C/N. Phương pháp giải Vận dụng lí thuyết điện trường Lời giải chi tiết Đơn vị của cường độ điện trường là V/m, N/C. Đáp án C 12.2 Đề bài: Những phát biểu nào sau đây là đúng? (1) Cường độ điện trường do điện tích điểm gây ra tại một điểm phụ thuộc vào độ lớn điện tích thử đặt tại điểm đó. (2) Vectơ cường độ điện trường tại mỗi điểm cùng chiều với lực tác dụng lên điện tích thử dương tại điểm đó. (3) Cường độ điện trường tại một điểm đặc trưng cho tác dụng lực của điện trường tại điểm đó. (4) Các đường sức của cùng một điện trường có thể cắt nhau. (5) Điện trường do điện tích âm gây ra trong không gian là điện trường đều. A. 2, 4 . B. 1, 3 . C. 2, 3 . D. 3, 4 . Phương pháp giải Vận dụng lí thuyết điện trường Lời giải chi tiết (1) – sai vì cường độ điện trường không phụ thuộc vào vào độ lớn điện tích thử đặt tại điểm đó. (4) – sai vì các đường sức không cắt nhau (5) – sai vì điện trường do điện tích âm không phải điện trường đều. Đáp án C 12.3 Đề bài: Chọn từ/cụm từ thích hợp trong bảng dưới đây để điền vào chỗ trống.
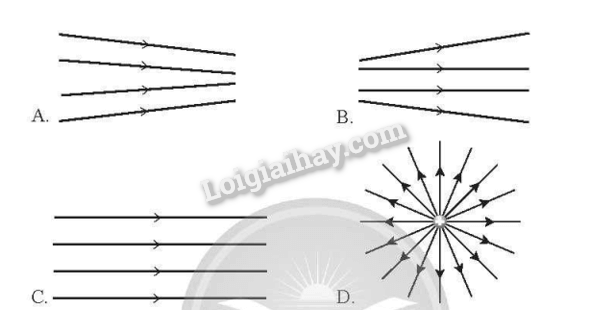
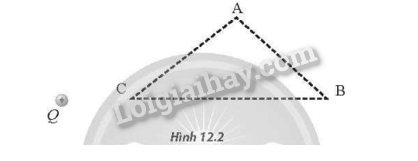
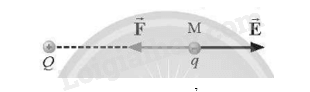
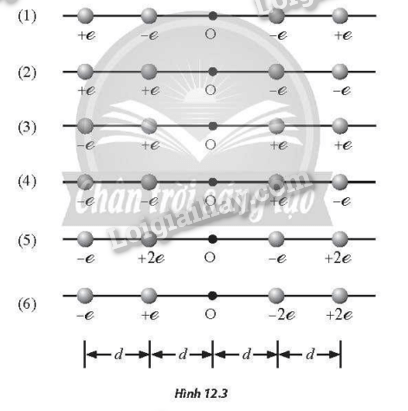
- Đường sức điện có các đặc điểm sau: + Tại mỗi điểm trong điện trường (1)... đường sức điện đi qua. Số lượng đường sức điện qua một đơn vị điện tích vuông góc với đường sức tại một điểm trong không gian đặc trưng cho (2) ... của điện trường tại điểm đó. + Các đường sức điện là những đường cong (3)... Đường sức điện phải bắt đầu từ một điện tích (4)... (hoặc ở vô cực) và kết thúc ở điện tích (5)... (hoặc ở vô cực). - Điện trường đều có các đường sức điện (6) ... và cách đều nhau. Phương pháp giải Vận dụng lí thuyết điện trường Lời giải chi tiết (1) chỉ có một; (2) độ mạnh yếu; (3) không kín; (4) dương; (5) âm, (6) song song. 12.4 Đề bài: Trong các hình dưới đây, hình nào biểu diễn điện trường đều? Phương pháp giải Vận dụng lí thuyết điện trường đều Lời giải chi tiết Điện trường đều là các đường thẳng song song cách đều nhau. Đáp án C 12.5 Đề bài: Cường độ điện trường do hai điện tích dương gây ra tại một điểm M lần lượt có độ lớn là 7 V/m và 15 V/m. Độ lớn cường độ điện trường tổng hợp tại M có thể nhận giá trị nào sau đây? A. 21 V/m . B. 23 V/m . C. 7 V/m . D. 5 V/m . Phương pháp giải Áp dụng công thức tính cường độ điện trường Lời giải chi tiết Độ lớn cường độ điện trường tổng hợp tại M: \(\left| {{E_1} - {E_2}} \right| \le {E_M} \le {E_1} + {E_2} \Rightarrow 8 \le {E_M} \le 22\) Đáp án A 12.6 Đề bài: Cường độ điện trường do một điện tích Q gây ra tại một điểm M là \(\overrightarrow E \). Đặt tại M một điện tích thử dương. Nếu ta thay điện tích thử ấy bằng một điện tích âm, độ lớn gấp 4 lần điện tích thử ban đầu thì cường độ điện trường tại M thay đổi như thế nào? A. Độ lớn không đổi, có chiều ngược chiều \(\overrightarrow E \). B. Độ lớn giảm 4 lần, có chiều ngược chiều \(\overrightarrow E \). C. Độ lớn giảm 4 lần, không đổi chiều. D. Không đổi. Phương pháp giải Sự phụ thuộc của cường độ điện trường vào điện tích thử Lời giải chi tiết Độ lớn cường độ điện trường không phụ thuộc vào điện tích thử. Đáp án D 12.7 Đề bài: Cho ba điểm A, B và C theo đúng thứ tự cùng nằm trên một đường sức điện của điện trường do điện tích q gây ra. Độ lớn cường độ điện trường tại A là 90 V/m, tại C là 5 V/m và Độ lớn cường độ điện trường tại B có độ lớn bằng bao nhiêu? A. 7 V/m. B. 21 V/m. C. 14 V/m. D. 9 V/m. Phương pháp giải Áp dụng công thức tính cường độ điện trường Lời giải chi tiết Gọi O là điểm ta đặt điện tích q, vì BA = 2BC nên ta suy ra 3OB = 2OC + OA . Vì E tỉ lệ nghịch với bình phương khoảng cách nên ta suy ra: \(\frac{3}{{\sqrt {{E_B}} }} = \frac{2}{{\sqrt {{E_C}} }} + \frac{1}{{\sqrt {{E_A}} }} \Rightarrow {E_B} \approx 9V/m\) Đáp án D Tự luận 12.1 Đề bài: Hình 12.1 mô tả đường sức điện của các điện tích. Hãy xác định dấu của các điện tích trong từng trường hợp. Phương pháp giải Dựa vào chiều đường sức điện Lời giải chi tiết Hình a: q1>0, q2<0; Hình b: q1>0,q2>0; Hình c: q < 0 . 12.2 Đề bài: Có thể dùng điện tích thử âm để khảo sát cường độ điện trường do điện tích điểm gây ra được không? Giải thích. Phương pháp giải Dựa vào mối quan hệ giữa điện tích thử và cường độ điện trường Lời giải chi tiết Vì cường độ điện trường do một điện tích điểm gây ra trong không gian không phụ thuộc vào điện tích thử nên ta có thể dùng điện tích thử âm. Khi đó, chiều của lực điện tác dụng lên điện tích thử ngược chiều với chiều vectơ cường độ điện trường. 12.3 Đề bài: Đặt một điện tích -3.10-6 C tại điểm A trong chân không. Xác định cường độ điện trường tại B, biết AB = 15 cm Phương pháp giải Áp dụng công thức tính cường độ điện trường Lời giải chi tiết Độ lớn cường độ điện trường tại B: \(E = \frac{{k\left| Q \right|}}{{{r^2}}} = \frac{{{{9.10}^9}.\left| { - {{3.10}^{ - 6}}} \right|}}{{0,{{15}^2}}} = {12.10^5}V/m\), hướng từ B về A 12.4 Đề bài: Một điện tích Q đặt trong chân không, cường độ điện trường tại điểm M cách Q là 20 cm, có độ lớn 450 V/m. Tính độ lớn của điện tích Q. Phương pháp giải Áp dụng công thức tính cường độ điện trường Lời giải chi tiết Độ lớn của điện tích: \(\left| Q \right| = \frac{{E{r^2}}}{k} = \frac{{450.0,{2^2}}}{{{{9.10}^9}}} = {2.10^{ - 9}}C\) 12.5 Đề bài: Sắp xếp độ lớn cường độ điện trường do điện tích điểm Q gây ra tại các điểm A, B, C (Hình 12.2) theo thứ tự tăng dần. Phương pháp giải Xác định cường độ điện trường tại các điểm Lời giải chi tiết Cường độ điện trường tỉ lệ nghịch với bình phương khoảng cách từ điểm đó đến điện tích nên EB<EA<EC 12.6 Đề bài: Hai điện tích điểm có giá trị điện tích lần lượt là +3,0μC và −5,0μC được đặt tại hai điểm M và N trong chân không. Khoảng cách giữa M và N là 0,2 m. Gọi P là điểm mà cường độ điện trường tổng hợp tại đó bằng 0. Hãy xác định vị trí điểm P. Phương pháp giải Áp dụng công thức tính cường độ điện trường Lời giải chi tiết Do hai điện tích tại M và N trái dấu nên điểm P nằm ngoài đoạn MN và gần M hơn (do độ lớn điện tích tại M nhỏ hơn độ lớn điện tích tại N). Ta có \(\left| {{E_1}} \right| = \left| {{E_2}} \right| \Rightarrow \frac{{k\left| {{q_1}} \right|}}{{M{P^2}}} = \frac{{k\left| {{q_2}} \right|}}{{{{(MP + 0,2)}^2}}} \Rightarrow \frac{3}{{M{P^2}}} = \frac{5}{{{{(MP + 0,2)}^2}}} \Rightarrow \left\{ \begin{array}{l}MP \approx 0,69m\\NP \approx 0,89m\end{array} \right.\) 12.7 Đề bài: Một electron tự do có điện tích và khối lượng lần lượt là −1,6.10−19C và 9,1.10−31 kg được đặt vào điện trường đều E = 300 V/m. Tính độ lớn gia tốc mà electron thu được dưới tác dụng của lực tĩnh điện. Phương pháp giải Áp dụng công thức tính lực điện và định luật 2 Newton Lời giải chi tiết Ta có: \(F = \left| q \right|E = ma\) Độ lớn gia tốc mà electron thu được dưới tác dụng của lực tĩnh điện là: \(a = \frac{{\left| q \right|E}}{m} = \frac{{\left| { - 1,{{6.10}^{ - 19}}} \right|.300}}{{9,{{1.10}^{ - 31}}}} \approx 5,{3.10^{13}}m/{s^2}\) 12.8 Đề bài: Đặt một điện tích Q=10−6Cvào một môi trường có hằng số điện môi bằng 3. a) Xác định vectơ cường độ điện trường tại điểm M cách Q là 2 cm. b) Đặt tại M một điện tích q=−2.10−8C. Xác định lực điện tác dụng lên q. Phương pháp giải Áp dụng công thức tính cường độ điện trường Lời giải chi tiết a) Độ lớn cường độ điện trường tại M: \(E = \frac{{k\left| Q \right|}}{{\varepsilon {r^2}}} = \frac{{{{9.10}^9}.\left| {{{10}^{ - 6}}} \right|}}{{3.0,{{02}^2}}} = 7,{5.10^6}V/m\) Hướng như hình vẽ: b) Độ lớn lực điện tác dụng lên q: \(F = \left| q \right|E = \left| { - {{2.10}^{ - 8}}} \right|.7,{5.10^6} = 0,15N\) Hướng như hình vẽ: 12.9 Đề bài: Cho hai điểm M và N cùng nằm trên một đường sức điện của điện trường do điện tích q gây ra. Độ lớn cường độ điện trường tại M là 45 V/m và tại N là 5 V/m. Độ lớn cường độ điện trường tại trung điểm I bằng bao nhiêu? Phương pháp giải Áp dụng công thức tính cường độ điện trường Lời giải chi tiết Gọi O là điểm ta đặt điện tích q, áp dụng các công thức tính cường độ điện trường tại M, N ta có: \(\left\{ \begin{array}{l}{E_M} = k\frac{{\left| q \right|}}{{O{M^2}}}\\{E_N} = k\frac{{\left| q \right|}}{{O{N^2}}}\end{array} \right. \Rightarrow \frac{{{E_M}}}{{{E_N}}} = \frac{{O{N^2}}}{{O{M^2}}} = \frac{{45}}{5} = 9 \Rightarrow ON = 3OM\) Ta có: \(\left\{ \begin{array}{l}OI = OM + \frac{{MN}}{2}\\MN = OI - OM = 2OM\end{array} \right. \Rightarrow OI = 2OM\) Độ lớn cường độ điện trường tại I: \({E_1} = k\frac{q}{{O{I^2}}} = k\frac{q}{{4O{M^2}}} = \frac{1}{4}{E_M} = \frac{1}{4}.45 = 11,25V/m\) 12.10 Đề bài: Có thể xem mô hình hạt nhân uranium là một quả cầu có bán kính 7,40.10-15 m. Biết hạt nhân uranium có 92 proton, điện tích của một hạt proton là 1,60.10-19 C. Xem gần đúng toàn bộ điện tích của hạt nhân uranium tập trung tại tâm của quả cầu. Hạt nhân uranium sau đó giải phóng một hạt α chứa 2 proton tại bề mặt của hạt nhân (hiện tượng phóng xạ). a) Tính cường độ điện trường tại bề mặt hạt nhân trước khi giải phóng hạt α b) Tính lực điện tác dụng lên hạt α tại bề mặt hạt nhân. Phương pháp giải Áp dụng công thức tính cường độ điện trường Lời giải chi tiết a) Cường độ điện trường trước khi phóng xạ: \(E = \frac{{k\left| q \right|}}{{{r^2}}} = \frac{{{{9.10}^9}.\left| {92.1,{{6.10}^{ - 19}}} \right|}}{{{{(7,{{4.10}^{ - 15}})}^2}}} \approx 2,{42.10^{21}}V/m\) b) Cường độ điện trường sau khi phóng xạ: \(E' = \frac{{k\left| {q'} \right|}}{{{r^2}}} = \frac{{{{9.10}^9}.\left| {(92 - 2).1,{{6.10}^{ - 19}}} \right|}}{{{{(7,{{4.10}^{ - 15}})}^2}}} \approx 2,{37.10^{21}}V/m\) Lực điện tác dụng lên hạt α: \(F = {q_\alpha }E' \approx 2.1,{60.10^{ - 19}}.2,{37.10^{21}} \approx 758{\rm{N}}\) 12.11 Đề bài: Hình 12.3 mô tả 6 trường hợp sắp xếp 4 điện tích điểm, trong đó các điện tích được đặt cách đều nhau bên trái và bên phải so với điểm O. Hãy sắp xếp độ lớn cường độ điện trường tại điểm O theo thứ tự tăng dần. Phương pháp giải Tổng hợp cường độ điện trường Lời giải chi tiết (1)<(3)<(4)<(5)=(6)<(2) Độ lớn cường độ điện trường tại điểm O trong các trường hợp:\({E_1} = 0,{E_2} = 2,5\frac{{ke}}{{{d^2}}},{E_3} = 0,5\frac{{ke}}{{{d^2}}},{E_4} = 2\frac{{ke}}{{{d^2}}},{E_5} = {E_6} = 2,25\frac{{ke}}{{{d^2}}}\)
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
|