Bài 9. Định luật Boyle trang 26, 27, 28 SBT Vật lí 12 Kết nối tri thứcQuá trình nào sau đây là đẳng quá trình?
Lựa chọn câu để xem lời giải nhanh hơn
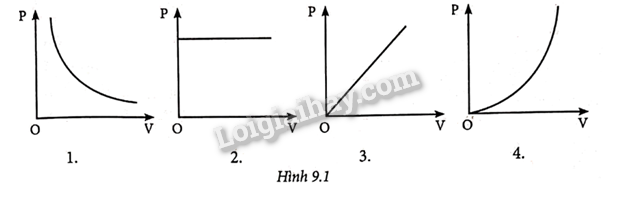
9.1 Quá trình nào sau đây là đẳng quá trình? A. Khí được đun nóng trong một bình kín. B. Khí trong một xi lanh được đun nóng đẩy pit-tông chuyển động. C. Không khí trong quả bóng bay được phơi ra nắng. D. Khí trong quả bóng thám không khi đang bay lên cao. Phương pháp giải: Vận dụng kiến thức về đẳng quá trình Lời giải chi tiết: Khí được đun nóng trong một bình kín: Trong trường hợp này, thể tích của khí không đổi vì bình kín. Khi đun nóng, áp suất và nhiệt độ của khí sẽ tăng, nhưng thể tích vẫn giữ nguyên. Đây chính là quá trình đẳng tích. Đáp án: A 9.2 Hệ thức nào sau đây là của định luật Boyle? A. \({p_1}{V_2} = {p_2}{V_1}.\) B. pV =hằng số. C. \(\frac{p}{V}\)= hằng số. D. \(\frac{V}{p}\)= hằng số. Phương pháp giải: Vận dụng kiến thức về quá trình đẳng nhiệt Lời giải chi tiết: Định luật Boyle: pV =hằng số. Đáp án: B 9.3 Đường biểu diễn nào sau đây biểu diễn mối liên hệ giữa thể tích V và áp suất p của một lượng khí xác định trong quá trình đẳng nhiệt?
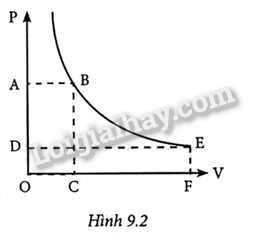
A. Chỉ đường 1. B. Đường 1, 2 và 3. C. Đường 2, 3 và 4. D. Đường 1, 3 và 4. Phương pháp giải: Vận dụng kiến thức về quá trình đẳng nhiệt Lời giải chi tiết: Trên đồ thị p-V, đường đẳng nhiệt là một đường hyperbol. Đồ thị 1: Đây là một đường hyperbol, thể hiện mối quan hệ tỉ lệ nghịch giữa áp suất và thể tích. Đây chính là đường đẳng nhiệt. Đáp án: A 9.4 Hình 9.2 là đồ thị biểu diễn đường đẳng nhiệt của một lượng khí lí tưởng. Sự so sánh nào sau đây giữa diện tích S1 của hình chữ nhật OABC với diện tích S2 của hình chữ nhật ODEF là đúng?
A. S1 > S2. B. S1 < S2. C. S1 ≈ S2. D. S1 = S2. Phương pháp giải: Vận dụng kiến thức về quá trình đẳng nhiệt Lời giải chi tiết: Có pV =hằng số \( \Rightarrow OA.OC = OD.{\rm{OF}}\) Vậy S1 = S2. Đáp án: D 9.5 Hãy dùng các số liệu trong bảng ghi kết quả thí nghiệm về quá trình đẳng nhiệt của một lượng khí không đổi ở ở hình bên để xác định mối quan hệ giữa áp suất và thể tích của lượng khí và vẽ đồ thị biểu diễn mối quan hệ này. Bảng ghi kết quả thí nghiệm về quá trình đẳng nhiệt của một lượng khí không đổi
Phương pháp giải: Vận dụng kiến thức về quá trình đẳng nhiệt Lời giải chi tiết: – Tính tích p.V của 4 trường hợp trong bảng để kết luận: pV = hằng số – Đồ thị là hình hyperbol.
9.6 Một xi lanh chứa 0,80 dm3 khi nitrogen ở áp suất 1,2 atm. Dùng pit-tông nén chậm khí này để tăng áp suất của nó lên 3,2 atm. Coi quá trình là đẳng nhiệt. 1. Tại sao phải nén chậm khí? 2. Khi áp dụng biểu thức của định luật Boyle, có cần đổi đơn vị thể tích và đơn vị áp suất ra Pa không? Tại sao? 3. Xác định thể tích cuối của khí. Phương pháp giải: Vận dụng kiến thức về quá trình đẳng nhiệt Lời giải chi tiết: 1. Phải nén chậm khí để có thể coi quá trình biến đổi trạng thái khí là đẳng nhiệt. 2. Không. Chỉ cần đơn vị của các đại lượng ở hai vế của phương trình giống nhau. 3. \({p_1}{V_1} = {p_2}{V_2} \Rightarrow {V_2} = \frac{{{p_1}{V_1}}}{{{p_2}}} = \frac{{1,2.0,8}}{{3,2}} = 0,3(d{m^3})\) 9.7 Để xác định độ sâu của một hồ nước, một người đã dùng cách cầm ngược một ống nghiệm theo phương thẳng đứng rồi lặn xuống đáy hồ và ghi lại mực nước dâng lên trong ống nghiệm khi ở đáy hồ. Hãy chứng minh rằng độ sâu của hồ sẽ được xác định bằng công thức: \(x = \frac{{p({h_1} - {h_2})}}{{Dg{h_2}}}\) Trong đó: x là độ sâu của hồ; p là áp suất khí quyển; D là khối lượng riêng của nước; g là gia tốc trọng trường; h1 là độ cao của ống nghiệm tức độ cao của cột khí trong ống nghiệm khi chưa lặn và h2 là độ cao của cột khí trong ống nghiệm khi ở đáy hồ. Phương pháp giải: Vận dụng kiến thức về quá trình đẳng nhiệt Lời giải chi tiết: Khi chưa lặn, áp suất không khí trong ống nghiệm bằng áp suất khí quyển \({p_1} = {p_{kq}}\); thể tích của không khí trong ống nghiệm là\({V_1} = {h_1}S\). Ở đáy hồ, áp suất của không khí trong ống nghiệm: \({p_2} = {p_{kq}} + {p_n}\)với\({p_n} = Dgh\); thể tích của không khí trong ống nghiệm là \({V_2} = {h_2}S\) Áp dụng định luật Boyle cho lượng không khí trong ống khi chưa lặn và khí ở đáy hồ có: \({p_1}{h_1} = {p_2}{h_2} \to {p_1}{h_1} = ({p_{kq}} + Dgh){h_2}\) Mà ta lại có: \({p_2}{h_2} = {p_1}{h_1} \to {p_2} = \frac{{{p_1}{h_1}}}{{{h_2}}}\) \( \Rightarrow {p_1}{h_1} = ({p_{kq}} + Dgh).\frac{{{p_1}{h_1}}}{{{h_2}}} \Rightarrow h = \frac{{({h_1} - {h_2}){p_{kq}}}}{{Dg{h_2}}}\) hay \(x = \frac{{p({h_1} - {h_2})}}{{Dg{h_2}}}\) 9.8 Người ta dùng bơm có pit-tông diện tích 8 cm2 và khoảng chạy 25 cm để bơm một bánh xe đạp sao cho khi áp lực của bánh lên mặt đường là 350 N thì diện tích tiếp xúc của bánh với mặt đường là 50 cm2. Ban đầu bánh chứa không khí có áp suất \({p_o} = {10^5}{\rm{ }}Pa\) và thể tích \({V_o} = 1500{\rm{ }}c{m^3}\). Giả thiết khi áp suất không khí trong bánh vượt quá 1,5po thì thể tích trong của xăm là 2 000 cm3 và nhiệt độ không khí trong xăm không đổi. 1. Phải đẩy bơm tối thiểu bao nhiêu lần? 2. Nếu do bơm hở nên mỗi lần đẩy bơm chỉ đưa được 100 cm3 không khí vào bánh xe thì phải đẩy bao nhiêu lần. Phương pháp giải: Vận dụng kiến thức về quá trình đẳng nhiệt Lời giải chi tiết: n = 10 lần; n' = 19 lần. 1. Áp suất không khí trong bánh khi bơm xong: \(p = {p_o} + p'\) với \(p' = \frac{{350}}{{0,005}} = {0,7.10^5}(Pa) \Rightarrow p = {1,7.10^5}Pa > 1,5{p_o}.\) Do đó sau khi bơm: \({V_2} = 2000c{m^3}\) Mỗi lần đẩy có \[8.25 = 200{\rm{ }}c{m^3}\]không khí được đưa vào bánh. Trạng thái 1: \({p_1} = {10^5}Pa;{V_1} = (1500 + 200n);{T_1} = T.\) Trạng thái 2: \({p_2} = {1,7.10^5}Pa;{V_2} = 2000c{m^3};{T_2} = T.\) Áp dụng định luật Boyle sẽ xác định được \(n = \frac{{19}}{2} \approx 10\)lần 2. Vì nếu bơm không khí hở thì mỗi lần đẩy đưa được 200 cm3 không khí vào bánh xe, còn khi bơm hở thì mỗi lần đẩy chỉ đưa được 100 cm3 vào bánh nên: \(n' = 2n = \frac{{19.2}}{2} = 19\)lần 9.9 Một xilanh chứa khí có pit-tông có thể trượt không ma sát dọc theo xi lanh. Biết pit-tông có khối lượng m, diện tích S, khí có thể tích ban đầu V và áp suất khí quyển là po. Xác định thể tích của khí khi xi lanh chuyển động theo phương thẳng đứng với gia tốc a. Coi nhiệt độ khí không đổi. Phương pháp giải: Vận dụng kiến thức về quá trình đẳng nhiệt Lời giải chi tiết: Khi xi lanh đi lên: \(V' = \frac{{mg + {p_o}S}}{{m(g + a) + {p_o}S}}V.\) Khi xi lanh đi xuống: \(V' = \frac{{mg + {p_o}S}}{{m(g - a) + {p_o}S}}V.\) Pit-tông ở trạng thái cân bằng chịu tác dụng của trọng lực, áp lực khí quyển và áp lực không khí trong xi lanh: \(\overrightarrow p + \overrightarrow {{f_1}} + \overrightarrow {{f_2}} = \overrightarrow 0 \Rightarrow p + {f_1} = {f_2} \Rightarrow mg + {p_0}S = pS \Rightarrow p = {p_0} + \frac{{mg}}{S}\) (1) Đây là quá trình đẳng tích nên: \(pV = p'V'.\) (2) Trong đó p, V là áp suất và thể tích của khí khi xi lanh đứng yên; p’, V’ là áp suất và thể tích của khí khi xi lanh chuyển động. Khi xi lanh chuyển động lên trên với gia tốc a thì nó chịu tác dụng thêm lực \(\overrightarrow {{f_a}} \) có chiều từ dưới lên. Do đó: \(p + {f_1} + {f_a} = {f_2} \Rightarrow m(g + a) + {p_o}S = p'S \Rightarrow p' = {p_o} + \frac{{m(g + a)}}{S}\) (3) Từ (1), (2), (3) rút ra: \(V' = \frac{{mg + {p_o}S}}{{m(g + a) + {p_o}S}}V\) Khi xi lanh chuyển động xuống dưới thì: \(V' = \frac{{mg + {p_o}S}}{{m(g - a) + {p_o}S}}V\) 9.10 Một quan niệm khác về cơ chế nổi lên và chìm xuống của cá. Đoạn văn sau đây có nội dung dựa theo bài “Công dụng của bong bóng cá” trong sách Vật lí vui của Ia.I.Perelman (NXB Giáo Dục, năm 2010). Quan niệm sau đây về cơ chế nổi lên và chìm xuống của cá đã được nhà khoa học Borenli người Italia nêu lên từ năm 1685. Muốn nổi lên, cá làm cho bóng bóng trong bụng phồng lên để lực đẩy Archimede tác dụng lên cá trở thành lớn hơn trọng lượng cá. Ngược lại, muốn chìm xuống, cá làm cho bong bóng xẹp xuống để lực đẩy Archimede tác dụng lên cá trở thành nhỏ hơn trọng lượng cá. Mọi người đều nghĩ quan niệm trên là đúng. Phải hơn 200 năm sau mới có người đưa ra một quan niệm khác về cơ chế này. Cá không thể chủ động làm thay đổi thể tích của bong bóng cá vì khi giải phẫu bong bóng cá, người ta không thấy có mô cơ. Sự thay đổi thể tích của bóng bóng cá do đó là tự động tuân theo các định luật về chất khí, cụ thể là định luật Boyle. Hãy dựa vào đoạn văn trên để trả lời các câu hỏi sau: 1. Để giải thích cơ chế nổi lên và chìm xuống của cá: A. Chỉ cần dùng định luật Boyle. B. Chỉ cần dùng định luật Archimede. C. Chỉ cần dùng tính chất phụ thuộc vào độ sâu của áp suất chất lỏng. D. Cần sử dụng tất cả các nội dung trên. 2. Nội dung câu nào dưới đây là đúng, sai?
3. Hãy dùng định luật Boyle để giải thích tại sao khi cá bơi lên thì bong bóng cá lại tự động phồng lên và ngược lại khi cá lặn xuống. 4. Hãy kể một hiện tượng thực tế chứng tỏ bong bóng cá phồng lên hay xẹp xuống là tự động tuân theo định luật Boyle. Phương pháp giải: Vận dụng kiến thức về quá trình đẳng nhiệt Lời giải chi tiết: 1. Để giải thích cơ chế nổi lên và chìm xuống của cá cần dùng định luật Boyle, định luật Archimede, tính chất phụ thuộc vào độ sâu của áp suất chất lỏng. 2. a) sai. “Muốn nổi lên, cá làm cho bóng bóng trong bụng phồng lên để lực đẩy Archimede tác dụng lên cá trở thành lớn hơn trọng lượng cá. Ngược lại, muốn chìm xuống, cá làm cho bong bóng xẹp xuống để lực đẩy Archimede tác dụng lên cá trở thành nhỏ hơn trọng lượng cá.” Nên bong bóng cá có tác dụng trong việc làm cho cá nổi lên hoặc chìm xuống. b) đúng. c) đúng. 3. Khi cá dùng đuôi và vây bơi lên thì vì áp suất của nước giảm theo độ sâu nên áp suất bên ngoài bong bóng cá giảm làm cho áp suất bên trong bong bóng cá giảm theo dẫn đến thể tích của bong bóng cá tăng và lực đẩy Archimede tác dụng lên cá cũng tăng giúp cá bơi lên mạnh hơn. Từ đây dễ dàng suy ra trường hợp cá lặn xuống. 4. Hãy tưởng tượng bạn đang lặn biển. Khi bạn lặn sâu hơn, bạn sẽ cảm thấy áp suất nước tác dụng lên cơ thể tăng lên đáng kể. Tương tự như vậy, bong bóng khí nhỏ trong tai bạn cũng sẽ bị nén lại do áp suất tăng. Đây chính là lý do tại sao chúng ta thường cảm thấy ù tai khi lặn sâu. Việc bong bóng cá phồng lên hay xẹp xuống khi cá bơi ở các độ sâu khác nhau là một ví dụ điển hình minh họa cho định luật Boyle trong thực tế. Sự thay đổi áp suất của nước tác động trực tiếp đến thể tích của bong bóng khí, khiến nó phồng lên hoặc xẹp xuống để duy trì một trạng thái cân bằng nhất định.
|
||||||||||||||||||