Bài tập cuối chương IV trang 84, 85, 86 SBT Vật lí 12 Kết nối tri thức

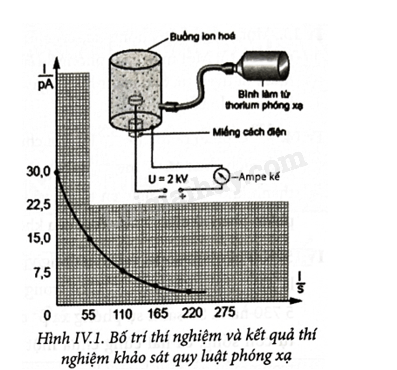
IV.1

Trong hạt nhân

A. có ba loại hạt là nucleon, proton và neutron.

B. có ba loại hạt là neutron, proton và electron.

C. có proton và neutron.

D. chỉ có neutron.

Phương pháp giải:

Vận dụng kiến thức về hạt nhân

Lời giải chi tiết:

Trong hạt nhân có proton và neutron.

Đáp án: C

IV.2

Tìm câu sai. Kí hiệu n là neutron, và p là proton. Trong hạt nhân có thể có trường hợp:

A. số n > số p.                                                   

B. số p > số n.

C. khi số n = 1 thì số p = 0.                               

D. khi số p = 1 thì số n = 0.

Phương pháp giải:

Vận dụng kiến thức về hạt nhân

Lời giải chi tiết:

Số p không thể bằng 0 vì nguyên tử có số lượng electron nhỏ nhất là Hydrogen (có 1 electron), thì số proton nhỏ nhất là 1.

Đáp án: C

IV.3

Trong hạt nhân \(_6^{14}C\)có

A. 6 proton và 8 electron.                                  

B. 6 proton và 8 neutron.

C. 6 proton và 14 electron.                                

D. 6 electron và 8 neutron.

Phương pháp giải:

Vận dụng kiến thức về hạt nhân

Lời giải chi tiết:

Trong hạt nhân \(_6^{14}C\)có Z = 6 proton và N = 14 – 6 = 8 neutron.

Đáp án: B

IV.4

Hai hạt nhân có tỉ số số khối là 8 và 27. Tỉ số hai bán kính của chúng là:

A. \(\frac{2}{3}\)                   

B. \(\frac{8}{{27}}\)  

C. \(\frac{4}{{15}}\)

D. \(\frac{4}{9}\)

Phương pháp giải:

Vận dụng kiến thức về hạt nhân

Lời giải chi tiết:

\(R = 1,{2.10^{ - 15}}{A^{\frac{1}{3}}} \Rightarrow \frac{{{R_1}}}{{{R_2}}} = \frac{{{8^{1/3}}}}{{{{27}^{1/3}}}} = \frac{2}{3}\)

Đáp án: A

IV.5

Thể tích nhỏ nhất có thể có của các hạt nhân là

A. 1,72.10^-30 m³.            

B. 7,23.10^-15 m³                     

C. 1, 23.10^-30 m³.            

D. 7,23.10^-45 m³.

Phương pháp giải:

Vận dụng kiến thức về hạt nhân

Lời giải chi tiết:

Hạt nhân của đồng vị hydrogen có số khối nhỏ nhất A = 1, đó là hạt nhân có thể tích nhỏ nhất. Bán kính của nó là: \({\rm{R}} = 1,2 \cdot {10^{ - 15}} \cdot {{\rm{A}}^{\frac{1}{3}}}\;{\rm{m}}\)

Coi hạt nhân có dạng hình cầu thì thể tích của nó là:

\({\rm{V}} = \frac{4}{3}\pi {{\rm{R}}^3} = \frac{4}{3}\pi {\left( {1,2 \cdot {{10}^{ - 15}} \cdot {{\rm{A}}^{\frac{1}{3}}}} \right)^3} = \frac{4}{3}\pi  \cdot 1,{2^3} \cdot {10^{ - 45}}\;{{\rm{m}}^3} \approx 7,23 \cdot {10^{ - 45}}\;{{\rm{m}}^3}\)

Đáp án: D

IV.6

Năng lượng liên kết riêng của một hạt nhân là năng lượng liên kết

A. tính riêng cho hạt nhân so với hạt nhân khác.

B. tính cho một nucleon trong hạt nhân.

C. của hai nucleon khác loại trong hạt nhân.

D. của hai nucleon cùng loại trong hạt nhân.

Phương pháp giải:

Vận dụng kiến thức về năng lượng liên kết riêng của hạt nhân

Lời giải chi tiết:

Năng lượng liên kết riêng của một hạt nhân là năng lượng liên kết tính cho một nucleon trong hạt nhân.

Đáp án: B

IV.7

Phóng xạ là quá trình:

A. hạt nhân phóng ra ra các hạt α, β^-, β⁺ khi bị bắn phá bằng các hạt nhân khác.

B. hạt nhân tự phát ra các hạt α, β^-, β⁺  và không biến đổi gì.

C. hạt nhân tự phát ra các hạt α, β^-, β⁺  và biến đổi thành một hạt nhân khác.

D. hạt nhân phát ra các bức xạ điện từ.

Phương pháp giải:

Vận dụng kiến thức về phóng xạ

Lời giải chi tiết:

Phóng xạ là quá trình tự phát, biến đổi thành hạt nhân khác đồng thời phát ra các tia phóng xạ.

Đáp án: C

IV.8

Trong một phản ứng phóng xạ, khi có tia α thì cũng có thể có:

A. tia β^-.                         

B. tia β⁺.                         

C. tia γ (gamma).           

D. các tia γ, β^-, β⁺ .

Phương pháp giải:

Vận dụng kiến thức về phóng xạ

Lời giải chi tiết:

Trong một phản ứng phóng xạ, khi có tia α thì cũng có thể có tia γ (gamma). 

Đáp án: C

IV.9

Khảo sát một bình ion hoá có cấu tạo là bình khí đơn phân tử và hai điện cực kim loại được đặt hiệu điện thế 2 kV. Khi khối khí này bị ion hoá nhờ tác dụng của tia phóng xạ thì sẽ có dòng điện chạy qua khối khí. Để đo dòng điện rất nhỏ này người ta dùng một ampe kế rất nhạy (Hình IV.1).

a) Vẽ đồ thị biểu diễn độ phóng xạ mẫu ²²⁰Rn trong bình theo thời gian, biết rằng độ phóng xạ tài thời điểm ban đầu là H₀.

b) Xác định chu kì bán rã của ²²⁰Rn.

c) Để dòng điện đủ lớn như trong thí nghiệm cần tối thiểu 1 mL lượng khí ²²⁰Rn ở điều kiện tiêu chuẩn. Hãy ước tính khối lượng tối thiểu của bình từ chất phóng xạ ²²⁸Th để duy trì độ phóng xạ không đổi của ²²⁰Rn trước khi làm thí nghiệm. Biết rằng:

²²⁸Th phân rã a với chu kì bán rã 1,9 năm thành ²²⁴Ra.

²²⁴Ra phân rã a với chu kì bán rã 3,6 ngày thành ²²⁰Rn.

Phương pháp giải:

Vận dụng kiến thức về phóng xạ

Lời giải chi tiết:

a) Vì độ phóng xạ tỉ lệ với cường độ dòng điện nên đồ thị cũng đồng dạng với đồ thị cường độ dòng điện Hình IV.1G.

b) Dựa vào đồ thị ta thấy tại các thời điểm 55 s; 110 s;… thì thu được các giá trị cường độ dòng điện giảm còn một nửa. Suy ra T = 55 s.

c) 1 mL khí ²²⁰Rn muốn duy trì độ phóng xạ thì lượng ²²⁰Rn bị mất đi phải được bù trừ bằng lượng ²²⁰Rn trong phân rã ²²⁴Ra. Và lượng ²²⁴Ra phải được bù trừ bằng lượng ²²⁴Ra tạo ra trong phân rã của ²²⁸Th. Chính vì vậy, để duy trì ta cần phải có: H_Th = H_Ra = H_Rn

1 mL khí ở điều kiện tiêu chuẩn có số mol là: \(n = \frac{V}{{22,4}} = \frac{{{{1.10}^{ - 3}}}}{{22,4}} = 4,{46.10^{ - 5}}mol\)

Số hạt  ²²⁰Rn là: \({N_{Rn}} = 4,{46.10^{ - 5}}.6,{02.10^{23}} = 2,{685.10^{19}}\)

\({H_{Rn}} = \lambda {N_{Rn}} = \frac{{\ln 2}}{T}.{N_{Rn}} = \frac{{\ln 2}}{{55}}.2,{685.10^{19}} = 3,{38.10^{17}}Ci = {H_{Th}}\)

\({N_{Th}} = \frac{{{H_{Th}}}}{{{\lambda _{Th}}}} = \frac{{3,{{38.10}^{17}}}}{{\frac{{\ln 2}}{{1,9.365.86400}}}} = 2,{92.10^{25}}\)

\({m_{Th}} = \frac{{{N_{Th}}}}{{{N_A}}}.A = \frac{{2,{{92.10}^{25}}}}{{6,{{02.10}^{23}}}}.228 = 11059\,g \approx 11\,kg\)

IV.10

Hoàn thành các phương trình phản ứng hạt nhân sau:

a) \(_7^{14}\;{\rm{N}} + _2^4{\rm{He}} \to _8^{17}{\rm{O}} + ?\)

b) \(_4^9{\rm{Be}} + _2^4{\rm{He}} \to _6^{12}{\rm{C}} + ?\)

c) \(_{29}^{64}{\rm{Cu}} \to _1^0{\rm{e}} + ?\)

d) \(_1^3{\rm{H}} \to _2^3{\rm{H}} + ?\)

Phương pháp giải:

Vận dụng kiến thức về phương trình phản ứng hạt nhân

Lời giải chi tiết:

a) \(_7^{14}\;{\rm{N}} + _2^4{\rm{He}} \to _8^{17}{\rm{O}} + _1^1{\rm{H}}\)

b) \(_4^9{\rm{Be}} + _2^4{\rm{He}} \to _6^{12}{\rm{C}} + _0^1{\rm{n}}\)

c) \(_{29}^{64}{\rm{Cu}} \to _1^0{\rm{e}} + _{28}^{64}{\rm{Ni}}\)

d) \(_1^3{\rm{H}} \to _2^3{\rm{H}} + _{ - 1}^0{\rm{e}}\)

IV.11

Cho các hạt nhân: \(_{13}^{27}{\rm{Al}};_{82}^{206}\;{\rm{Pb}}.\) Biết m_Al = 26,98153 amu; m_Pb = 205,9745 amu; m_p = 1,00728 amu; m_n = 1,00866 amu; 1 amu = 931,5 MeV/c².

a) Tính độ hụt khối của mỗi hạt nhân.

b) Tính năng lượng liên kết riêng của mỗi hạt nhân và cho biết hạt nhân nào bền vững hơn.

Phương pháp giải:

Vận dụng kiến thức về năng lượng liên kết riêng của hạt nhân

Lời giải chi tiết:

a) Độ hụt khối của hạt nhân Al: \(\Delta {\rm{m}} = \left( {13\;{{\rm{m}}_{\rm{p}}} + 14\;{{\rm{m}}_{\rm{n}}}} \right) - {{\rm{m}}_{{\rm{Al}}}} = 13 \cdot 1,00728 + 14 \cdot 1,00866 - 26,98153 = 0,23435{\rm{amu}}\)

Độ hụt khối của hạt nhân Pb: \(\Delta {\rm{m}} = \left( {82\;{{\rm{m}}_{\rm{p}}} + 124\;{{\rm{m}}_{\rm{n}}}} \right) - {{\rm{m}}_{{\rm{Pb}}}} = 82 \cdot 1,00728 + 124 \cdot 1,00866 - 205,9745 = 1,6963{\rm{amu}}.\)

b) Năng lượng liên kết riêng của hạt nhân Al: \(\frac{{\Delta {{\rm{m}}_{{\rm{Al}}}}{{\rm{c}}^2}}}{{\;{{\rm{A}}_{{\rm{Al}}}}}} = \frac{{0,23435.931,5}}{{27}} = 8,085075{\rm{MeV}}\)

Năng lượng liên kết riêng của hạt nhân Pb: \(\frac{{\Delta {{\rm{m}}_{{\rm{Pb}}}}.{c^2}}}{{\;{{\rm{A}}_{{\rm{Pb}}}}}} = \frac{{1,6963.931,5}}{{206}} = 7,6704051{\rm{MeV}}.\)

⇒ Al bền vững hơn hạt nhân Pb.

IV.12

Một phòng thí nghiệm ban đầu mua về một mẫu phóng xạ nguyên chất có khối lượng m₀. Chu kì bán rã của mẫu chất đó là 3 465 giây.

a) Tính hằng số phóng xạ của mẫu chất phóng xạ đó.

b) Sau bao lâu (tính từ lúc mua) thì 75% chất đó đã biến thành chất khác.

Phương pháp giải:

Vận dụng kiến thức về phóng xạ

Lời giải chi tiết:

a) Hằng số phóng xạ: \(\lambda  = \frac{{\ln 2}}{{\;{\rm{T}}}} = {2.10^{ - 4}}\;{{\rm{s}}^{ - 1}}\)

b) Khoảng thời gian để 75% chất đó đã biến thành chất khác (tức là số hạt nhân chưa phân rã còn lại là \(25\% \;{{\rm{N}}_0}\)):

Theo định luật phóng xạ: \({\rm{N}}\left( {\rm{t}} \right) = {{\rm{N}}_0}{2^{ - \frac{t}{T}}} \Rightarrow \frac{{{\rm{N}}\left( {\rm{t}} \right)}}{{{{\rm{N}}_0}}} = {2^{ - \frac{t}{{3465}}}} = 0,25 \Rightarrow t = 6930\,s.\)

IV.13

Một mẫu chất phóng xạ, có chu kì bán rã 2 ngày, gồm 6,4.10¹¹ hạt nhân nguyên tử. Một mẫu chất phóng xạ khác, có chu kì bán rã 3 ngày, gồm 8.10¹⁰ hạt nhân nguyên tử. Sau bao nhiêu ngày số hạt nhân nguyên tử chưa phóng xạ của hai mẫu đó bằng nhau?

Phương pháp giải:

Vận dụng kiến thức về phóng xạ

Lời giải chi tiết:

Tại thời điểm t, hai mẫu có số hạt nhân còn lại như nhau: \({N_1} = {N_2}\)

\( \Rightarrow {N_{01}} \cdot {2^{ - \frac{t}{{{T_1}}}}} = {N_{02}}{2^{ - \frac{t}{{{T_2}}}}} \Rightarrow {2^{ - \frac{t}{{{T_1}}} + \frac{t}{{{T_2}}}}} = \frac{{{N_{02}}}}{{{N_{01}}}} = \frac{1}{8} \Rightarrow t\left( {\frac{1}{{{T_1}}} - \frac{1}{{\;{{\rm{T}}_2}}}} \right) = 3 \Rightarrow t = \frac{3}{{\frac{1}{{\;{{\rm{T}}_1}}} - \frac{1}{{\;{{\rm{T}}_2}}}}} = 18\)

Sau 18 ngày hai mẫu có số hạt nhân còn lại như nhau.

IV.14

²³⁸U phân rã thành ²⁰⁶Pb với chu kì bán rã 4,47.10⁹ năm. Một khối đá được phát hiện chứa 46,97 mg ²³⁸U và 23,15 mg ²⁰⁶Pb. Giả sử khối đá khi mới hình thành không chứa nguyên tố chì và tất cả lượng chì có mặt trong đó đều là sản phẩm phân rã của ²³⁸U. Tuổi của khối đá đó hiện nay là bao nhiêu?

Phương pháp giải:

Vận dụng kiến thức về phân rã

Lời giải chi tiết:

Số hạt nhân U đã bị phân rã bằng số hạt nhân Pb tạo thành:

\(\Delta {\rm{N}} = \frac{{{{\rm{m}}_{{\rm{Pb}}}}}}{{{{\rm{A}}_{{\rm{Pb}}}}}} \cdot {{\rm{N}}_{\rm{A}}} = \frac{{23,{{15.10}^{ - 3}}}}{{206}}.6,{02.10^{23}} = 6,{76.10^{19}}\) (hạt)

Số hạt nhân U còn lại là: \({\rm{N}} = \frac{{{{\rm{m}}_U}}}{{{{\rm{A}}_U}}} \cdot {{\rm{N}}_{\rm{A}}} = \frac{{46,{{97.10}^{ - 3}}}}{{238}}.6,{02.10^{23}} = 11,{9.10^{19}}\) (hạt)

Tại thời điểm hiện phát hiện:

 \(\frac{{\Delta {\rm{N}}}}{{\rm{N}}} = \frac{{{N_0}\left( {1 - {2^{ - \frac{{\rm{t}}}{{\rm{T}}}}}} \right)}}{{{N_0}{2^{ - \frac{{\rm{t}}}{{\rm{T}}}}}}} \Rightarrow {2^{\frac{{\rm{t}}}{{4,{{47.10}^9}}}}} - 1 = 0,568 \Rightarrow t = 2,{9.10^9}\) năm.

IV.15

Khi cây còn sống, tỉ lệ hai đồng vị ¹²C và ¹⁴C trong nó và trong khí quyển là như nhau. Khi chết, ¹⁴C có trong cây bị phân rã. Chu kì bán rã của ¹⁴C là 5 730 năm. So sánh sự phóng xạ ββ^- của một mẫu gỗ cổ với một mẫu gỗ tương tự còn sống, cả hai cùng chứa một lượng ¹⁴C người ta thấy số hạt ¹⁴C có trong mẫu gỗ cổ ít hơn 3 lần so với mẫu gỗ tương đương còn đang sống. Xác định tuổi của mẫu gỗ cổ.

Phương pháp giải:

Vận dụng kiến thức về chu kì bán rã

Lời giải chi tiết:

Cả hai có cùng lượng \(_6^{12}{\rm{C}}\)nên lượng \(_6^{14}{\rm{C}}\)ban đầu là như nhau.

Định luật phóng xạ: \({N_t} = {N_0} \cdot {2^{ - \frac{t}{T}}} \Rightarrow {2^{ - \frac{t}{T}}} = \frac{{{N_t}}}{{{N_0}}} = \frac{1}{3} \Rightarrow t = 9081,8\) năm

IV.16

Tiêm 10 cm³ dung dịch chứa đồng vị phóng xạ ²⁴Na với nồng độ 10^-3 mol/L vào tĩnh mạch của người. Sau 6 giờ lấy 10 cm³ máu của người đó thì thấy có 1,5.10^-8 mol ²⁴Na trong đó. Tính thể tích V của máu có trong người. Cho chu kì bán rã của ²⁴Na là 15 h

Phương pháp giải:

Vận dụng kiến thức về chu kì bán rã

Lời giải chi tiết:

Ta có: \(10\;{\rm{c}}{{\rm{m}}^3} = {10^{ - 2}}\;{\rm{L}}.\)

Với nồng độ \({10^{ - 3}}\;{\rm{mol}}/{\rm{L}}\), số mol ²⁴Na tiêm vào người là: \({n_0} = {10^{ - 2}} \cdot {10^{ - 3}} = {10^{ - 5}}\;{\rm{mol}}\)

Sau t = 6h, số mol có trong người là: \({\rm{n}} = {{\rm{n}}_0}{{\rm{e}}^{ - \lambda {\rm{t}}}}.\)

Với T = 15h, cho ta: \(\lambda  = \frac{{0,693}}{{\;{\rm{T}}}} = \frac{{0,693}}{{15}}.\)

Từ đó xác định được trong V lít máu của người có: \({\rm{n}} = {10^{ - 5}}{{\rm{e}}^{ - \frac{{0,693}}{{15}} \cdot 6}} = 0,{75.10^{ - 5}}\;{\rm{mol}}.\)

Trong V lít máu có \(0,75 \cdot {10^{ - 5}}\;{\rm{mo}}{{\rm{l}}^{24}}{\rm{Na}}.\)Trong \({10^{ - 2}}\;{\rm{L}}\) có \(1,5 \cdot {10^{ - 8}}\;{\rm{mo}}{{\rm{l}}^{24}}{\rm{Na}}.\)

Vậy \({\rm{V}} = \frac{{0,75 \cdot {{10}^{ - 5}} \cdot {{10}^{ - 2}}}}{{1,5 \cdot {{10}^{ - 8}}}} = 5\;{\rm{L}}.\)

IV.17

Giả sử quả bom nguyên tử thả xuống Hiroshima có chứa 100 kg quặng uranium trong đó \(_{92}^{235}{\rm{U}}\)chiếm 25%. Nếu trung bình mỗi phân hạch của \(_{92}^{235}{\rm{U}}\)giải phóng 200 MeV thì năng lượng giải phóng của vụ nổ tương đương bao nhiêu số điện? Lấy khối lượng 1 mol \(_{92}^{235}{\rm{U}}\)bằng 235 g.

Phương pháp giải:

Vận dụng kiến thức về năng lượng nguyên tử

Lời giải chi tiết:

Số hạt nhân nguyên tử có trong 100 kg quặng uranium:

\({\rm{N}} = \frac{{100 \cdot 25 \cdot 6,023 \cdot {{10}^{23}}}}{{100 \cdot 0,235}} \approx 640,745 \cdot {10^{23}}\) hạt.

1 MeV = 1,6.10^-13 J.

Năng lượng toả ra của vụ nổ \({\rm{W}} = 640,745 \cdot {10^{23}} \cdot 200.{\rm{1,6}}{\rm{.1}}{{\rm{0}}^{ - 13}} = 2050,384 \cdot {10^{12}}\;{\rm{J}}{\rm{.\;}}\)

Số số điện tương đương: \({\rm{n}} = \frac{{2050,384 \cdot {{10}^{12}}}}{{3,6 \cdot {{10}^6}}} \approx 5,{7.10^8}{\rm{kWh}}.\)

IV.18

Một nhà máy điện nguyên tử tiêu thụ trung bình 58,75 g \(_{92}^{235}{\rm{U}}\)mỗi ngày. Biết hiệu suất của nhà máy là 25%; mỗi hạt nhân nguyên tử phân hạch giải phóng 200 MeV.

a) Hãy tính công suất phát điện của nhà máy.

b) Giả thiết sau mỗi phân hạch trung bình có 2,5 neutron được giải phóng thì sau một ngày số neutron thu được trong lò phản ứng là bao nhiêu?

Cho: N_A = 6,023.10²³ hạt/mol; 1 MeV = 1,6.10^-13 J.

Phương pháp giải:

Vận dụng kiến thức về phản ứng phân hạch

Lời giải chi tiết:

a) Năng lượng giải phóng do phân hạch của 58,75 g \(_{92}^{235}{\rm{U}}\)

\({\rm{W}} = \frac{{58,75 \cdot 6,023 \cdot {{10}^{23}} \cdot 200}}{{235}} = 301,1 \cdot {10^{23}}{\rm{MeV}} = 481,76 \cdot {10^{10}}\;{\rm{J}}\)

Công suất điện của nhà máy: \(P = \frac{{{\rm{W}}{\rm{.H}}}}{t} = \frac{{481,76 \cdot {{10}^{10}}.25}}{{100 \cdot 24 \cdot 3600}} \approx 13,94 \cdot {10^6}\;W = 13,94MW.\)

b) Số neutron giải phóng do 58,75 g \(_{92}^{235}{\rm{U}}\):

\({{\rm{N}}_1} = \frac{{58,75 \cdot 6,023 \cdot {{10}^{23}} \cdot 2,5}}{{235}} = 3,{76438.10^{23}}\)hạt

Số neutron bị hấp thụ để 58,75 g \(_{92}^{235}{\rm{U}}\) phân hạch hết:

\({{\rm{N}}_2} = \frac{{58,75 \cdot 6,023 \cdot {{10}^{23}}}}{{235}} = 1,5057 \cdot {10^{23}}\)hạt

Số neutron thu được trong lò phản ứng: \({\rm{N}} = {{\rm{N}}_1} - {{\rm{N}}_2} = 2,25862 \cdot {10^{23}}\) hạt.