Bài 23. Hiện tượng phóng xạ trang 78, 79, 80 SBT Vật lí 12 Kết nối tri thứcĐánh dấu (x) vào các cột (đúng) hoặc (sai) tương ứng với các nội dung trong bảng dưới đây
Lựa chọn câu để xem lời giải nhanh hơn
23.1 Đánh dấu (x) vào các cột (đúng) hoặc (sai) tương ứng với các nội dung trong bảng dưới đây
Phương pháp giải: Vận dụng kiến thức về phóng xạ Lời giải chi tiết:
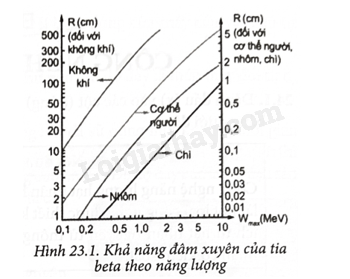
23.2 Tìm phát biểu sai. A. Khi đi qua điện trường giữa hai bản tụ điện, tia α bị lệch về phía bản mang điện âm của tụ điện. B. Hạt α là hạt nhân nguyên tử helium. C. Tia α làm ion hoá môi trường. D. Tia α đi qua điện trường giữa hai bản tụ điện sẽ bị lệch về phía bản mang điện dương của tụ điện. Phương pháp giải: Vận dụng kiến thức về phóng xạ Lời giải chi tiết: Tia α đi qua điện trường giữa hai bản tụ điện sẽ bị lệch về phía bản mang điện dương của tụ điện. Đáp án: D 23.3 Tìm phát biểu sai. A. Hạt β- là hạt electron. B. Tia β- có khả năng ion hoá môi trường. C. Trong điện trường giữa hai bản tụ điện, tia β- bị lệch về phía bản mang điện dương của tụ điện. D. Tia β- có tầm bay ngắn hơn tia α. Phương pháp giải: Vận dụng kiến thức về phóng xạ Lời giải chi tiết: Tia β- có tốc độ lớn hơn, khả năng đâm xuyên lớn hơn, do đó tầm bay xa hơn tia α. Đáp án: D 23.4 Tìm phát biểu sai A. Tia β+ có tầm bay xa hơn tia α. B. Hạt β+ có cùng khối lượng với electron nhưng mang điện tích nguyên tố dương. C. Tia β+ cũng làm ion hoá môi trường nhưng yếu hơn tia α. D. Tia β+ bị lệch về phía bản mang điện dương của tụ điện khi đi qua điện trường giữa hai bản tụ điện. Phương pháp giải: Vận dụng kiến thức về phóng xạ Lời giải chi tiết: Tia β+ bị lệch về phía bản mang điện âm của tụ điện khi đi qua điện trường giữa hai bản tụ điện. Đáp án: D 23.5 Công thức nào dưới đây đúng với nội dung của định luật phóng xạ? A. \({\rm{m}} = {{\rm{m}}_0}{{\rm{e}}^{\lambda {\rm{t}}}}.\) B. \({\rm{m}} = {{\rm{m}}_0}{{\rm{e}}^{ - \lambda {\rm{t}}}}.\) C. \(m = {m_0}{e^{ - \frac{\lambda }{t}}}.\) D. \({\rm{m}} = {{\rm{m}}_0}{{\rm{e}}^{ - \frac{{\rm{t}}}{{\rm{T}}}}}.\) Phương pháp giải: Vận dụng kiến thức về phóng xạ Lời giải chi tiết: Công thức của định luật phóng xạ: \({\rm{m}} = {{\rm{m}}_0}{{\rm{e}}^{ - \lambda {\rm{t}}}}.\) Đáp án: B 23.6 Một mẫu phóng xạ có chu kì bán rã là 3 ngày. Sau 9 ngày, khối lượng của mẫu phóng xạ này còn lại là 2 kg. Khối lượng ban đầu của mẫu là bao nhiêu? A. 15 kg. B. 16 kg. C. 17 kg. D. 14 kg. Phương pháp giải: Vận dụng kiến thức về phóng xạ Lời giải chi tiết: Từ công thức \({\rm{m}} = {{\rm{m}}_0}{2^{ - \frac{t}{T}}} \Rightarrow 2 = {m_0}{.2^{ - \frac{9}{3}}} \Rightarrow {m_0} = 16\) Đáp án: B 23.7 Chu kì bán rã của một mẫu phóng xạ là 6 giờ. Lúc đầu mẫu có khối lượng 2,4.10-2 kg. Hỏi sau một ngày đêm, khối lượng của mẫu còn lại bằng bao nhiêu? A. 3.10-3 kg. B. 1,5.10-3 kg. C. 2,5.10-3 kg. D. 2,10-3 kg. Phương pháp giải: Vận dụng kiến thức về phóng xạ Lời giải chi tiết: Áp dụng công thức \({\rm{m}} = {{\rm{m}}_0}{2^{ - \frac{t}{T}}} = 2,{4.10^{ - 2}}{.2^{ - \frac{{24}}{6}}} = 1,{5.10^{ - 4}}kg.\) Đáp án: B 23.8 Sau 3 giờ phóng xạ, số hạt nhân của một mẫu đồng vị phóng xạ chỉ còn 25% số hạt nhân ban đầu. Chu kì bán rã của đồng vị này là A. 1 giờ. B. 2 giờ. C. 2,5 giờ. D. 1,5 giờ. Phương pháp giải: Vận dụng kiến thức về bán rã Lời giải chi tiết: Áp dụng công thức \(m = {m_0}{.2^{ - \frac{t}{T}}} \Rightarrow 0,25{m_0} = {m_0}{.2^{ - \frac{3}{T}}} \Rightarrow T = 1,5\) giờ Đáp án: D 23.9 Một chất phóng xạ lúc đầu có 40 mg; chu kì bán rã là 10 giờ. Hỏi sau bao lâu thì khối phóng xạ trên còn 10 mg A. 10 giờ. B. 5 giờ. C. 20 giờ. D. 40 giờ. Phương pháp giải: Vận dụng kiến thức về phóng xạ Lời giải chi tiết: Áp dụng công thức \({\rm{m}} = {{\rm{m}}_0}{.2^{ - \frac{t}{T}}} \Rightarrow 10 = {40.2^{ - \frac{t}{{10}}}} \Rightarrow t = 20\)giờ Đáp án: C 23.10 Dựa vào đồ thị đâm xuyên của tia beta (Hình 23.1) hãy so sánh khả năng đâm xuyên của tia beta trong không khí, cơ thể người, nhôm và chì?
Phương pháp giải: Vận dụng kiến thức về phóng xạ Lời giải chi tiết: Khả năng đâm xuyên của tia beta từ mạnh đến yếu, tương ứng với khoảng cách đâm xuyên của tia beta từ lớn đến nhỏ là: Không khí, cơ thể người, nhôm và chì. Ví dụ: Vẽ một đường thẳng, thẳng đứng ứng với tia beta có động năng 0,5 MeV, nó cắt các đường đồ thị của không khí, cơ thể người, nhôm và chì lần lượt ở các điểm có hoành độ là 120 cm, 22 cm, 6 cm và 2 cm. Có nghĩa là tia beta có động năng 0,5 MeV có thể xuyên qua 120 cm không khí hoặc 22 cm cơ thể người, hoặc 7 cm nhôm, hoặc 2 cm chì. 23.11 Hình 23.2 là ảnh chụp hai vết của tia alpha xuất phát từ một mẫu phóng xạ kích thước rất nhỏ được đặt trong buồng sương. Nhận xét đặc điểm hai vết này? Biết rằng buồng sương được đặt trong một từ trường có đường sức từ vuông góc với mặt phẳng ảnh h chụp, hãy xác định chiều của từ trường? Phương pháp giải: Vận dụng kiến thức về phóng xạ Lời giải chi tiết: Hạt α là các hạt mang điện dương, khi hạt mang điện dương chuyển động tạo thành một dòng điện. Vì hai vết chuyển động co ở phía dưới và mở rộng ở phía trên nên nguồn phóng xạ được đặt ở phía dưới góc phải của hình. Do vậy các hạt α đi từ dưới lên và lệch trái. Nó tương ứng với dòng điện đi từ dưới lên trên và bị lực từ tác dụng sang phía trái. Theo quy tắc bàn tay trái có thể suy ra từ trường vuông góc với mặt phẳng hình chụp và hướng từ người quan sát đi vào mặt phẳng hình chụp. 23.12 Chứng minh rằng, sau thời gian t = xT, T là chu kì bán rã, thì số hạt nhân phóng xạ còn lại là \({\rm{N}} = \frac{{{{\rm{N}}_0}}}{{{2^{\rm{x}}}}}\) Phương pháp giải: Vận dụng kiến thức về phóng xạ Lời giải chi tiết: Từ định luật phân rã phóng xạ \({\rm{N}} = {{\rm{N}}_0}{2^{ - \frac{t}{T}}} = {N_0}{.2^{ - \frac{{xT}}{T}}} = {N_0}{.2^{ - x}} = \frac{{{N_0}}}{{{2^x}}}\) 23.13 Sau 1 năm trong 1 miligam 144Ce có 2,5.1018 hạt bị phân rã. Hỏi chu kì bán rã của 144Ce bằng bao nhiêu? Phương pháp giải: Vận dụng kiến thức về bán rã Lời giải chi tiết: Số nguyên tử chứa trong 1mg 144C là: \({{\rm{N}}_0} = \frac{{{m_0}}}{A}.{N_A} = \frac{{{{10}^{ - 3}}}}{{144}}.6,{023.10^{23}} = 4,182 \cdot {10^{18}}\) Số nguyên tử bị phân rã trong thời gian t là: \(\Delta {\rm{N}} = {{\rm{N}}_0}\left( {1 - {2^{ - \frac{t}{T}}}} \right) \Rightarrow 2,{5.10^{18}} = 4,{182.10^{18}}.\left( {1 - {2^{ - \frac{1}{T}}}} \right) \Rightarrow T = 0,76\) năm 23.14 Một tượng cổ bằng gỗ có độ phóng xạ H. Một mảnh gỗ của cây vừa mới chặt, nếu có khối lượng tương đương sẽ có độ phóng xạ là 1,5H. Chu kì bán rã của 14C là 5 600 năm. Tính tuổi của tượng gỗ cổ này. Phương pháp giải: Vận dụng kiến thức về bán rã Lời giải chi tiết: Ta có \({\rm{H}} = {{\rm{H}}_0}{.2^{ - \frac{t}{T}}} \Rightarrow H = 1,5H{.2^{ - \frac{t}{{5600}}}} \Rightarrow t = 3276\) năm. Vậy tuổi của tượng gỗ là 3276 năm. 23.15 Để xác định lượng máu trong bệnh nhân, người ta tiêm vào máu một người một lượng nhỏ dung dịch chứa đồng vị phóng xạ 24Na (chu kì bán rã 15 giờ) có độ phóng xạ 2 μμCi. Sau 7,5 giờ người ta lấy ra 1 cm3 máu người đó thì thấy có độ phóng xạ 502 phân rã/phút. Tính thể tích máu của người đó. Phương pháp giải: Vận dụng kiến thức về phóng xạ Lời giải chi tiết: Đổi \({{\rm{H}}_0} = 2\mu {\rm{Ci}} = 2 \cdot {10^{ - 6}} \cdot 3,7 \cdot {10^{10}} = 7,4 \cdot {10^4}\;{\rm{Bq}}\) \(H = 502.V = \frac{{502}}{{60}}V = 8,37.V\)phân rã/phút (V là thể tích của máu: \({\rm{c}}{{\rm{m}}^3}\)) \({\rm{H}} = {{\rm{H}}_0}{2^{ - \frac{{\rm{t}}}{{\rm{T}}}}} = {{\rm{H}}_0}{2^{ - \frac{{7,5}}{{15}}}} \Rightarrow \frac{{\rm{H}}}{{{{\rm{H}}_0}}} = {2^{ - 0,5}} = \frac{{8,37\;{\rm{V}}}}{{7,4 \cdot {{10}^4}}}\) \( \Rightarrow {\rm{V}} = 6251,6\;{\rm{c}}{{\rm{m}}^3} = 6,25{\rm{d}}{{\rm{m}}^3} = 6,25\;{\rm{L}}.\)
|