Bài 16. Từ thông. Hiện tượng cảm ứng điện từ trang 49, 50, 51 SBT Vật lí 12 Kết nối tri thứcPhát biểu nào sau đây về từ thông là không đúng? A. Từ thông là đại lượng vectơ, được xác định bằng số đường sức từ xuyên qua tiết diện của cuộn dây. B. Từ thông là đại lượng vô hướng, được sử dụng để diễn tả số đường sức từ xuyên qua diện tích S nào đó. C. Đơn vị của từ thông là vêbe, kí hiệu là Wb. D. Từ thông qua diện tích S nào đó bằng không khi vectơ pháp tuyến của diện tích S vuông góc với vectơ cảm ứng từ của từ trường.
Lựa chọn câu để xem lời giải nhanh hơn
16.1 Phát biểu nào sau đây về từ thông là không đúng? A. Từ thông là đại lượng vectơ, được xác định bằng số đường sức từ xuyên qua tiết diện của cuộn dây. B. Từ thông là đại lượng vô hướng, được sử dụng để diễn tả số đường sức từ xuyên qua diện tích S nào đó. C. Đơn vị của từ thông là vêbe, kí hiệu là Wb. D. Từ thông qua diện tích S nào đó bằng không khi vectơ pháp tuyến của diện tích S vuông góc với vectơ cảm ứng từ của từ trường. Phương pháp giải: Vận dụng kiến thức về từ thông Lời giải chi tiết: A – sai vì từ thông là đại lượng vô hướng. Đáp án: A 16.2 Phát biểu nào sau đây là đúng khi nói về hiện tượng cảm ứng điện từ? A. Hiện tượng cảm ứng điện từ chỉ tồn tại trong khoảng thời gian có từ thông biến thiên. B. Khi có từ thông biến thiên qua cuộn dây dẫn thì luôn có dòng điện cảm ứng xuất hiện trong cuộn dây, ngay cả khi cuộn dây không kín. C. Hiện tượng cảm ứng điện từ không xảy ra trong khối vật dẫn, kể cả khi có từ thông biến thiên qua khối vật dẫn đó. D. Dòng điện cảm ứng chạy trong cuộn dây dẫn kín không gây ra tác dụng nhiệt đối với cuộn dây. Phương pháp giải: Vận dụng kiến thức về hiện tượng cảm ứng điện từ Lời giải chi tiết: B – sai vì cuộn dây không kín thì không có dòng điện. C – sai vì trong khối vật dẫn mà có dòng điện chạy qua, có từ thông qua khối vật dẫn biến thiên thì vẫn xuất hiện hiện tượng cảm ứng điện từ. D – sai vì dòng điện có tác dụng nhiệt (nhiều hay ít tuỳ vào bản chất kim loại dẫn). Đáp án: A
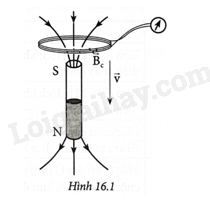
16.3 Cách nào sau đây không làm cho từ thông qua tiết diện vòng dây dẫn kín biến thiên? A. Quay vòng dây cắt ngang các đường cảm ứng từ của nam châm vĩnh cửu. B. Dịch chuyển nam châm sao cho các đường sức từ dịch chuyển song song với mặt phẳng khung dây. C. Đặt mặt phẳng cuộn dây cạnh nam châm điện xoay chiều. D. Cho nam châm vĩnh cửu rơi qua lòng cuộn dây. Phương pháp giải: Vận dụng kiến thức về hiện tượng cảm ứng điện từ Lời giải chi tiết: B sai vì số đường sức từ qua mặt phẳng khung dây trong trường hợp này không đổi. Đáp án: B 16.4 Nối hai đầu cuộn dây dẫn kín với điện kế và cho chuyển động rơi tự do qua một nam châm (Hình 16.1). Biết cảm ứng từ, đường sức từ của nam châm được mô tả như hình vẽ và khi bắt đầu chuyển động, kim điện kế chỉ vạch số 0.
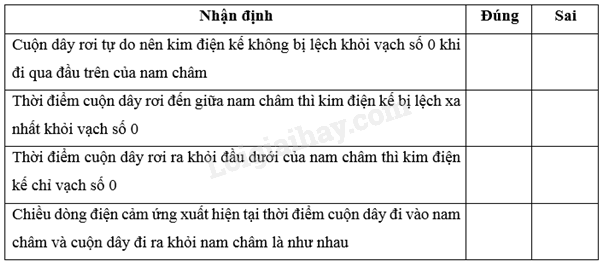
Nhận định nào sau đây là đúng hay sai?
Phương pháp giải: Vận dụng kiến thức về hiện tượng cảm ứng điện từ Lời giải chi tiết:
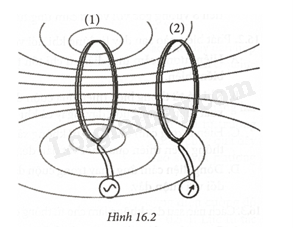
Giải thích: - Cuộn dây chuyển động rơi tự do, số đường sức từ qua cuộn dây biến thiên nên kim điện kế bị lệch do có dòng điện cảm ứng xuất hiện trong cuộn dây. - Khi cuộn dây rơi đến giữa nam châm thì số đường sức từ qua cuộn dây là ít nhất nên kim điện kế bị lệch ít nhất. - Thời điểm cuộn dây rơi ra khỏi đầu dưới của nam châm thì kim điện kế bị lệch nhiều nhất. - Chiều của dòng điện cảm ứng xuát hiện tại thời điểm cuộn dây đi vào nam châm và cuộn dây đi ra khỏi nam châm là ngược chiều nhau. 16.5 Đặt hai cuộn dây dẫn kín cạnh nhau như Hình 16.2. Một cuộn nối với nguồn điện. Một cuộn nối với điện kế, khi không có dòng điện chạy trong cuộn dây thì kim điện kế chỉ vạch số 0.
Nhận định nào sau đây là đúng hay sai?
Phương pháp giải: Vận dụng kiến thức về hiện tượng cảm ứng điện từ Lời giải chi tiết:
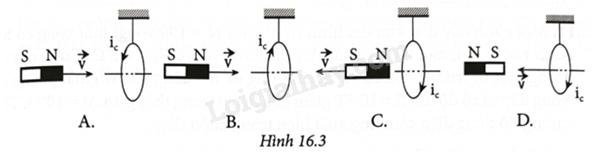
Giải thích: - Kim điện kế bị lệch khỏi vạch số 0 khi nguồn điện là nguồn điện một chiều là sai vì từ thông qua cuộn dây không biến thiên. - Mắc cuộn dây với nguồn điện một chiều và dịch chuyển cuộn dây ra xa thì kim điện kế vẫn không bị lệch khỏi vạch số 0 là sai vì khi dịch chuyển cuộn dây thì từ thông qua cuộn dây biến thiên. 16.6 Trường hợp nào trong Hình 16.3 xác định đúng chiều dòng điện cảm ứng trong vòng dây dẫn kín?
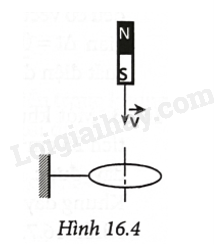
Phương pháp giải: Vận dụng kiến thức về quy tắc nắm bàn tay phải và định luật Lenz. Lời giải chi tiết: Dựa vào quy tắc nắm bàn tay phải và định luật Lenz. Dòng điện cảm ứng sinh ra có chiều chống lại nguyên nhân sinh ra nó. Đáp án: B 16.7 Khi cho nam châm rơi qua vòng dây như Hình 16.4.
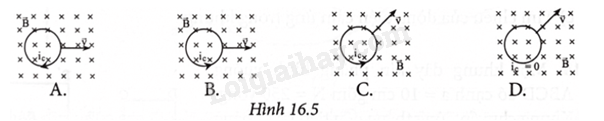
Nhận xét nào sau đây là đúng nếu nhìn vòng dây theo hướng từ dưới lên? A. Lúc đầu, dòng điện cảm ứng cùng chiều kim đồng hồ. Khi nam châm xuyên qua vòng dây, dòng điện cảm ứng đổi chiều ngược chiều kim đồng hồ. B. Lúc đầu, dòng điện cảm ứng ngược chiều kim đồng hồ. Khi nam châm xuyên qua vòng dây, dòng điện cảm ứng không đổi chiều. C. Không có dòng điện cảm ứng trong vòng dây khi nam châm đi vào hoặc đi ra khỏi vòng dây. D. Dòng điện cảm ứng xuất hiện trong vòng dây luôn cùng chiều kim đồng hồ. Phương pháp giải: Vận dụng kiến thức về hiện tượng cảm ứng điện từ Lời giải chi tiết: Dòng điện cảm ứng khi nam châm đi vào và đi ra khỏi cuộn dây có chiều ngược nhau. Đáp án: A 16.8 Trường hợp nào trong Hình 16.5 là đúng khi cho vòng dây tịnh tiến với vận tốc \({\rm{\vec v}}\) trong từ trường đều?
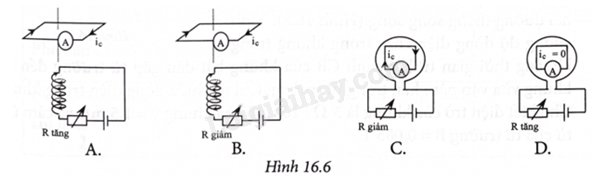
Phương pháp giải: Vận dụng kiến thức về quy tắc bàn tay trái Lời giải chi tiết: Trường hợp D là đúng khi cho vòng dây tịnh tiến với vận tốc \({\rm{\vec v}}\) trong từ trường đều Đáp án: D 16.9 Trường hợp nào trong Hình 16.6 xác định đúng chiều dòng điện cảm ứng trong khung dây dẫn?
Phương pháp giải: Vận dụng kiến thức về quy tắc nắm bàn tay phải và định luật Lenz Lời giải chi tiết: Dựa vào quy tắc nắm bàn tay phải và định luật Lenz. Dòng điện cảm ứng sinh ra có chiều chống lại nguyên nhân sinh ra nó Đáp án: A 16.10 Một hình vuông cạnh 5 cm đặt trong từ trường đều có cảm ứng từ B = 8.10-4 T. Từ thông qua hình vuông đó bằng 10-6 Wb. Tính góc hợp bởi vectơ cảm ứng từ với mặt phẳng của hình vuông đó. Phương pháp giải: Vận dụng kiến thức về hiện tượng cảm ứng điện từ Lời giải chi tiết: Diện tích khung dây: \({\rm{S}} = 25 \cdot {10^{ - 4}}\;{{\rm{m}}^2}.\) Áp dụng công thức tính từ thông: \(\Phi = {\rm{BS}}\cos \alpha \Rightarrow {10^{ - 6}} = {8.10^{ - 4}}{.25.10^{ - 4}}.\cos \alpha \Rightarrow \cos \alpha = \frac{1}{2} \Rightarrow \alpha = \pm \frac{\pi }{3}.\) Trong đó α là góc tạo bởi vectơ pháp tuyến của mặt phẳng hình vuông và vectơ cảm ứng từ, nên góc tạo bởi vectơ cảm ứng từ với mặt phẳng hình vuông là: \(\beta = \frac{\pi }{2} - \alpha = \frac{\pi }{6}\) hoặc \(\frac{{5\pi }}{6}.\) Do góc hợp bởi vectơ cảm ứng từ với mặt phẳng của hình vuông là góc nhọn, nên chọn \(\beta = \frac{\pi }{6}.\)
16.11 Một cuộn dây dẫn kín, dẹt hình tròn, gồm N = 100 vòng, mỗi vòng có bán kính r = 10 cm, mỗi mét dài của dây dẫn có điện trở R0 = 0,5 W. Cuộn dây đặt trong một từ trường đều có vectơ cảm ứng từ \({\rm{\vec B}}\) vuông góc với mặt phẳng các vòng dây và có độ lớn B = 10-2 T giảm đều đến 0 trong thời gian ∆t = 10-2 s. Tính cường độ dòng điện cảm ứng xuất hiện trong cuộn dây. Phương pháp giải: Vận dụng kiến thức về hiện tượng cảm ứng điện từ Lời giải chi tiết: Từ thông qua một vòng dây của cuộn dây là: \(\Phi = {\rm{BS}}\cos \alpha \), trong đó \(\alpha = 0\)và \({\rm{S}} = \pi {{\rm{r}}^2}.\) Xét trong khoảng thời gian từ \({{\rm{t}}_0} = 0\) đến thời điểm t, từ thông qua 1 vòng dây thay đổi từ \({\Phi _0}\) đến \({\Phi _t}\)ứng với cảm ứng từ là \({{\rm{B}}_0} = {10^{ - 2}}\;{\rm{T}}\) và \({{\rm{B}}_{\rm{t}}} = 0.\) Theo định luật Faraday ta có suất điện động qua N vòng dây của cuộn dây là: \({\rm{e}} = - {\rm{N}}\frac{{\Delta \Phi }}{{\Delta {\rm{t}}}} = - {\rm{NS}}\frac{{\Delta {\rm{B}}}}{{\Delta {\rm{t}}}}\) Cường độ dòng điện xuất hiện trong cuộn dây là: \(i = \frac{e}{R}\) Trong đó, \({\rm{R}} = {\rm{L}}{{\rm{R}}_0} = {\rm{N}}2\pi {\rm{r}}{{\rm{R}}_0}\) là điện trở của khung dây. Do đó, \({\rm{i}} = - {\rm{N}}\pi {{\rm{r}}^2}\frac{{\frac{{\Delta {\rm{B}}}}{{\Delta {\rm{t}}}}}}{{{\rm{N}}2\pi {\rm{r}}{{\rm{R}}_0}}} = - \frac{{\rm{r}}}{{2{{\rm{R}}_0}}} \cdot \frac{{\Delta {\rm{B}}}}{{\Delta {\rm{t}}}} = - \frac{{0,1}}{{2 \cdot 0,5}} \cdot \frac{{0 - {{10}^{ - 2}}}}{{{{10}^{ - 2}}}} = 0,1\;{\rm{A}}.\) 16.12 Một khung dây dẫn hình vuông, cạnh a = 10 cm, đặt cố định trong từ trường đều có vectơ cảm ứng từ \(\overrightarrow B \) vuông góc với mặt phẳng khung. Trong khoảng thời gian ∆t = 0,05 s, cho độ lớn của \(\overrightarrow B \) tăng đều từ 0 đến 0,5 T. Xác định độ lớn của suất điện động cảm ứng xuất hiện trong khung. Phương pháp giải: Vận dụng kiến thức về suất điện động Lời giải chi tiết: Ta có \(\alpha = 0\) và \(N{\rm{ }} = {\rm{ }}1,\)nên \(\left| {\rm{e}} \right| = \left| { - {\rm{N}}\frac{{\Delta \Phi }}{{\Delta {\rm{t}}}}} \right| = \left| { - {\rm{S}}\frac{{\Delta {\rm{B}}}}{{\Delta {\rm{t}}}}} \right| = \left| { - 0,{1^2} \cdot \frac{{0,5}}{{0,05}}} \right| = 0,1V.\) 16.13 Một khung dây cứng, phẳng diện tích 25 cm2, gồm 10 vòng dây. Khung dây được đặt trong từ trường đều. Khung dây nằm trong mặt phẳng như Hình 16.7. Cảm ứng từ biến thiên theo thời gian theo đồ thị.
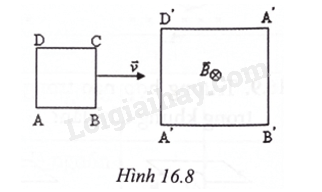
a) Tính độ biến thiên của từ thông qua khung dây kể từ lúc t = 0 đến t = 0,4 s. b) Xác định suất điện động cảm ứng trong khung. c) Tìm chiều của dòng điện cảm ứng trong khung. Phương pháp giải: Vận dụng kiến thức về suất điện động Lời giải chi tiết: a) Tại thời điểm \({t_0} = 0\) thì \({B_0} = 2,4 \cdot {10^{ - 3}}\;{\rm{T}}\); thời điểm t = 0,4s thì \({{\rm{B}}_{\rm{t}}} = 0\;{\rm{T}}\) và góc α=0. Do đó, ta có \(\Delta \Phi = {\Phi _{\rm{t}}} - {\Phi _0} = {\rm{NS}}.\Delta {\rm{B}} = 10 \cdot 25 \cdot {10^{ - 4}} \cdot \left( {0 - 2,4 \cdot {{10}^{ - 3}}} \right) = - {6.10^{ - 5}}\;{\rm{Wb}}.\) b) Theo định luật Faraday ta có: \({\rm{e}} = \left| { - \frac{{\Delta \Phi }}{{\Delta {\rm{t}}}}} \right| = \frac{{6 \cdot {{10}^{ - 5}}}}{{0,4}} = 1,5 \cdot {10^{ - 4}}\;{\rm{V}} = 0,15{\rm{mV}}.\) c) Cảm ứng từ B giảm nên theo định luật Lenz cảm ứng từ do dòng điện cảm ứng sinh ra sẽ cùng chiều với cảm ứng từ B. Theo quy tắc bàn tay phải, tìm được chiều dòng điện cảm ứng theo chiều kim đồng hồ chạy trong cuộn dây. 16.14 Một khung dây kín phẳng hình vuông ABCD có cạnh a = 10 cm gồm N = 250 vòng. Khung chuyển động thẳng đều tiến lại khoảng không gian trong đó có từ trường. Trong khi chuyển động cạnh AB và DC luôn nằm trên hai đường thẳng song song (Hình 16.8). Tính cường độ dòng điện chạy trong khung trong khoảng thời gian từ khi cạnh CB của khung bắt đầu gặp từ trường đến khi khung vừa vặn nằm hẳn trong từ trường. Chỉ rõ chiều dòng điện trong khung. Cho biết điện trở của khung là 3 Ω. Tốc độ của khung v = 1,5 m/s và cảm ứng từ của từ trường B = 0,005 T.
Phương pháp giải: Vận dụng kiến thức về suất điện động Lời giải chi tiết: Tại thời điểm \({t_0} = 0\)khi khung dây có cạnh BC bắt đầu vào vùng từ trường đều thì diện tích khung dây nằm trong từ trường \({{\rm{S}}_0} = 0\) và thời điểm t thì diện tích khung dây vào trong từ trường là \({{\rm{S}}_{\rm{t}}} = {\rm{BC}}.vt = avt\) và góc α = 0 ⇒ từ thông qua 1 vòng của khung dây là \({\Phi _t} = {\rm{B}}{{\rm{S}}_{\rm{t}}} = Bav.\Delta t\) Theo định luật Faraday ta có: \({\rm{e}} = - {\rm{N}}\frac{{\Delta \Phi }}{{\Delta {\rm{t}}}} = {\rm{N}}\frac{{{\rm{Bav}} \cdot \Delta {\rm{t}}}}{{\Delta {\rm{t}}}} = {\rm{NBav}} = 250.0,005.0,1.1,5 = 0,1875\;{\rm{V}}.\) Lại có \(i = \frac{e}{R} = \frac{{NBav}}{R} = \frac{{0,1875}}{3} = 0,0625\;{\rm{A}} = 62,5\;{\rm{mA}}.\) Khi khung dây đi vào vùng từ trường, từ thông qua khung dây tăng, nên cảm ứng từ do dòng điện cảm ứng sinh ra ngược chiều với cảm ứng từ của vùng từ trường, do đó, chiều dòng điện qua khung theo chiều ngược chiều kim đồng hồ hay chiều từ A đến B. 16.15 Một khung dây hình chữ nhật có các cạnh lần lượt là: a = 10 cm; b = 20 cm gồm 50 vòng dây quay đều trong một từ trường đều có cảm ứng từ B = 0,5 T. Trục quay của khung nằm vuông góc với đường sức từ. Lúc đầu, mặt phẳng khung vuông góc với vectơ cảm ứng từ. Khung quay với tốc độ góc ωω = 100p (rad/s). Tính suất điện động trung bình trong khung dây trong thời gian nó quay được 15° kể từ vị trí ban đầu. Phương pháp giải: Vận dụng kiến thức về suất điện động Lời giải chi tiết: Tại thời điểm \({{\rm{t}}_0} = 0:\alpha = 0\); tại thời điểm \({\rm{t}}:\alpha = \omega {\rm{t}} = \frac{\pi }{{12}}{\rm{rad}}\) nên \({\rm{t}} = \frac{1}{{12}} \cdot {10^{ - 2}}\;{\rm{s}}\) ⇒ từ thông qua mỗi vòng dây là: \(\Phi = {\rm{BS}}\cos \alpha \) Theo định luật Faraday ta có: \(e = - N\frac{{\Delta \Phi }}{{\Delta t}} = - NBS\frac{{\cos \frac{\pi }{{12}} - \cos 0}}{{\Delta t}} = - 50.0,5 \cdot 0,1 \cdot 0,2\frac{{\cos \frac{\pi }{{12}} - \cos 0}}{{\frac{1}{{12}} \cdot {{10}^{ - 2}}}} = 6,5\;{\rm{V}}\)
|