Giải mục 4 trang 69, 70, 71, 72 SGK Toán 11 tập 2 - Cùng khám phá

Hoạt động 8

Trong mặt phẳng \(\left( \alpha  \right)\), vẽ một hình vuông ABCD, gọi O là giao điểm của AC và BD.

- Qua O, vẽ dường thẳng a vuông góc với \(\left( \alpha  \right)\).

- Trên đường thẳng a lấy điểm S khác O. So sánh độ dài các đoạn thẳng SA, SB, SC, SD và rút ra nhận xét về hình dạng các mặt bên của hình chóp S.ABCD.

Phương pháp giải:

Chứng minh tam giác SAC, SBD cân tại S và SA = SB.

Lời giải chi tiết:

 

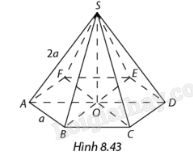
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot AC,SO \bot BD\)

O là giao điểm AC và BD của hình vuông ABCD nên O là trung điểm của AC, BD

Suy ra tam giác SAC cân tại S, tam giác SBD cân tại S

Nên SA = SC, SB = SD

Ta có: \(SA = \sqrt {A{O^2} + S{O^2}} ,SB = \sqrt {B{O^2} + S{O^2}} \)

ABCD là hình vuông nên AO = BO

Suy ra SA = SB = SC = SD.

Luyện tập 6

Cho hình chóp lục giác đều S.ABCDEF có cạnh bên bằng 2a và cạnh đáy bằng a (Hình 8,43). Gọi O là tâm của đáy. Tính SO.

Phương pháp giải:

Đáy là hình lục giác nên AO = a. Áp dụng định lý Py-ta-go để tính SO.

Lời giải chi tiết:

ABCDEF là lục giác đều nên AO = a

Xét tam giác SAO vuông tại O có:

\(SO = \sqrt {S{A^2} + A{O^2}}  = \sqrt {{a^2} + {a^2}}  = \sqrt 2 a\)

Hoạt động 9

Cho hình chóp tam giác đều S.ABC. Gọi A’, B’, C’ lần lượt là trung điểm của các cạnh SA, SB, SC (Hình 8,44).

a) Mặt phẳng (A’B’C’) có song song với mặt phẳng (ABC) không? Vì sao?

b) Tam giác A’B’C’ có phải là tam giác đều không? Vì sao?

c) Các tứ giác ABB'A', BCC’B’, ACC’A’ có hình dạng đặc biệt gì?

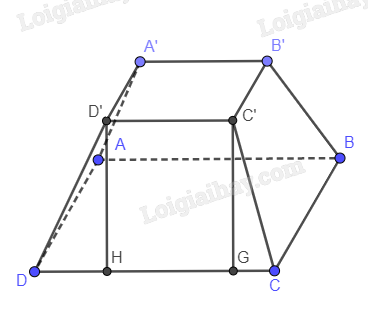
Phương pháp giải:

a) Nếu mặt phẳng (P) chứa đường thẳng a, b cắt nhau và cùng song song với (Q) thì (P) song song với (Q).

b) Đường trung bình của tam giác song song với cạnh thứ ba và bằng một nửa cạnh đó.

c) Hình thang là tứ giác có 2 cạnh đáy song song với nhau.

Lời giải chi tiết:

a) A’, B’ là trung điểm của SA, SB nên A’B’ song song với AB

A’, C’ là trung điểm của SA, SC nên A’C’ song song với AC

(A’B’C’) song song với (ABC) vì A’B’ song song với AB, A’C’ song song với AC.

b) A’, B’ là trung điểm của SA, SB nên A’B’ = \(\frac{1}{2}\)AB

A’, C’ là trung điểm của SA, SC nên A’C’ = \(\frac{1}{2}\)AC

B’, C’ là trung điểm của SB, SC nên B’C’ = \(\frac{1}{2}\)BC

Mà AB = AC = CA nên A’B’ = A’C’ = C’A’

Vậy A’B’C’ là tam giác đều.

c) ABB’A’ là hình thang vì AB song song với A’B’

BCC’B’ là hình thang vì BC song song với B’C’

ACC’A’ là hình thang vì AC song song với A’C’.

Luyện tập 7

Cho hình chóp cụt tứ giác đều ABCD.AB’C’D’ có cạnh đáy lớn bằng 3a, cạnh đáy nhỏ bằng a, cạnh bên bằng 2a. Tính chiều cao của hình chóp cụt đều này.

Phương pháp giải:

Kẻ C’H, D’G vuông góc với CD. Suy ra C’H song song với D’G. Tính CH và áp dụng định lý Py-ta-go để tính C’H.

Lời giải chi tiết:

Kẻ D’H, C’G vuông góc với CD. Suy ra D’H song song với C’G

Mà C’D’ song song với CD

Suy ra D’C’GH là hình chữ nhật

\( \Rightarrow HG = C'G' = a\)

\( \Rightarrow DH + GC = 2a \Rightarrow DH = GC = a\)

Xét tam giác D’HD vuông tại H có:

\(D'H = \sqrt {DD{'^2} - D{H^2}}  = \sqrt {{{\left( {2a} \right)}^2} - {a^2}}  = \sqrt 3 a\)