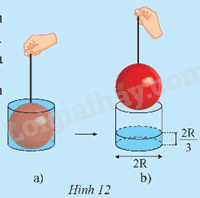
Giải mục 3 trang 96 SGK Toán 9 tập 2 - Chân trời sáng tạo

HĐ4

Trả lời câu hỏi Hoạt động 4 trang 96 SGK Toán 9 Chân trời sáng tạo

Một quả cầu có bán kính R nằm khít trong chiếc bình hình trụ đổ đầy nước có chiều cao h = 2R (Hình 12a). Rút qua cầu ra khỏi bình nước, ta thấy chiều cao của mực nước bằng $\frac{1}{3}$ chiều cao h (Hình 12b). Hãy tính theo R:

a) Thể tích của chiếc bình hình trụ;

b) Thể tích của nước ở trong bình;

c) Thể tích của hình cầu.

Phương pháp giải:

Dựa vào công thức thể tích của hình trụ: V = S.h = $\pi$r²h

Lời giải chi tiết:

a) Thể tích của chiếc bình hình trụ V = S.h = $\pi$R².2R = 2$\pi$R³

b) Thể tích của nước ở trong bình là:

V_nước = S.h = $\pi {R^2}.\frac{{2R}}{3} = \frac{2}{3}\pi {R^3}$ 

c) Thể tích của hình cầu là:

V_cầu = V_trụ - V_nước = $\frac{4}{3}\pi {R^3}$. 

TH3

Trả lời câu hỏi Thực hành 3 trang 96 SGK Toán 9 Chân trời sáng tạo

Một quả bóng rổ (khi bơm căng) có đường kính 24 cm (Hình 14). Tìm thể tích của quả bóng rổ đó (kết quả làm tròn đến hàng đơn vị).

Phương pháp giải:

Dựa vào công thức thể tích của hình cầu có bán kính R là: V = $\frac{4}{3}\pi {R^3}$.

Lời giải chi tiết:

Bán kính quả bóng là: R = $\frac{d}{2} = \frac{{24}}{2}$ = 12 cm.

Thể tích của quả bóng rổ là: V = $\frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {.12^3} \approx$ 7238 (cm³).