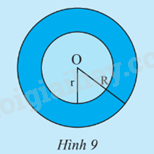
Giải mục 3 trang 101 SGK Toán 9 tập 1 - Chân trời sáng tạo

HĐ3

Trả lời câu hỏi Hoạt động 3 trang 101 SGK Toán 9 Chân trời sáng tạo

a) Vẽ đường tròn (C) tâm O bán kính r = 5 cm và đường tròn (C’) tâm O bán kính R = 8 cm.

b) Tính diện tích S của (C) và diện tích S’ của (C’).

c) Hãy cho biết hiệu số (S’ – S) biểu diễn diện tích của phần nào trên Hình 9.

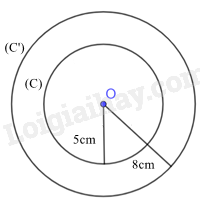
Phương pháp giải:

-  Đọc kĩ dữ kiện để vẽ hình.

-  Dựa vào công thức diện tích đường tròn S =$\pi$R²

Lời giải chi tiết:

a) Ta có hình vẽ:

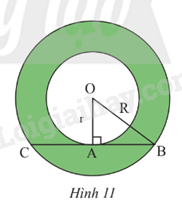
b) Diện tích S của (C) là: $S = 5^2\pi  = 25\pi \approx 78,54 (cm^2)$

Diện tích S’ của (C’) là $S’ = 8^2\pi = 64\pi \approx 201,06 (cm^2)$

c) Hiệu số (S’ – S) biểu diễn diện tích của phần tô màu xanh đậm trong hình 9.

TH3

Trả lời câu hỏi Thực hành 3 trang 101 SGK Toán 9 Chân trời sáng tạo

Tính diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; 10 cm) và (O; 20 cm) (kết quả làm tròn đến hàng phần trăm)

Phương pháp giải:

-  Đọc kĩ dữ kiện để vẽ hình.

-  Áp dụng diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) là: $S = \pi ({R^2} - {r^2})$

Lời giải chi tiết:

Diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; 10 cm) và (O; 20 cm) là:

$S = \pi ({R^2} - {r^2}) = \pi ({20^2} - {10^2}) = 300\pi  \approx 942,48$ cm².

VD3

Trả lời câu hỏi Vận dụng 3 trang 101 SGK Toán 9 Chân trời sáng tạo

Cho hình vành khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) với R > r. Trên đường tròn (O; R) lấy hai điểm B, C sao cho BC vừa là dây cung của (O; R), vừa là tiếp tuyến của đường tròn (O; r) tại A (Hình 11)

a) Tính độ dài đoạn thẳng BC theo r và R.

b) Cho BC = $a\sqrt 3$. Tính diện tích hình khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) theo a.

Phương pháp giải:

-  Dựa vào tính chất tiếp tuyến chứng minh OA $\bot$BC

-  Tính BC bằng cách áp dụng định lý pythagore trong tam giác vuông

-  Áp dụng diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) là: $S = \pi ({R^2} - {r^2})$

Lời giải chi tiết:

a) Vì BC là tiếp tuyến của đường tròn (O; r) tại A nên OA $\bot$BC

Xét tam giác OAB vuông tại A , ta có:

AB = $\sqrt {O{B^2} - O{A^2}}  = \sqrt {{R^2} - {r^2}}$ (theo định lý Pythagore)

Tương tự với tam giác OCA vuông tại A, ta có

AC = $\sqrt {O{C^2} - O{A^2}}  = \sqrt {{R^2} - {r^2}}$ (theo định lý Pythagore)

Vậy BC = AB + AC = 2$\sqrt {{R^2} - {r^2}}$.

b) Ta có BC = 2$\sqrt {{R^2} - {r^2}}$ = $a\sqrt 3$ suy ra $\sqrt {{R^2} - {r^2}}$ = $\frac{{a\sqrt 3 }}{2}$

Diện tích hình khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) theo a là:

$S = \pi ({R^2} - {r^2})$ = $\pi {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = \frac{{3\pi }}{4}{a^2}$.