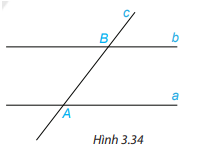
Giải mục 2 trang 52, 53 SGK Toán 7 tập 1 - Kết nối tri thứcVẽ hai đường thẳng song song a,b. Kẻ đường thẳng c cắt đường thẳng a tại A và cắt đường thẳng b tại B. Trên Hình 3.34:.. Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên...
Lựa chọn câu để xem lời giải nhanh hơn
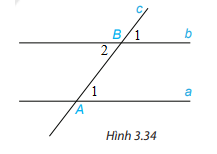
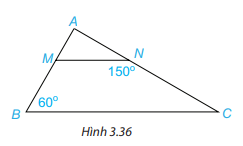
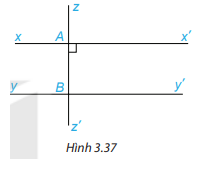
HĐ 2 Vẽ hai đường thẳng song song a,b. Kẻ đường thẳng c cắt đường thẳng a tại A và cắt đường thẳng b tại B. Trên Hình 3.34: a) Em hãy đo một cặp góc so le trong rồi rút ra nhận xét. b) Em hãy đo một cặp góc đồng vị rồi rút ra nhận xét. Phương pháp giải: a) Chọn một cặp góc ở vị trí so le trong rồi đo góc. b) Chọn một cặp góc ở vị trí đồng vị rồi đo góc. Lời giải chi tiết: a) Ta có: \(\widehat {{B_2}}\) và \(\widehat {{A_1}}\) là hai góc ở vị trí so le trong. Đo góc ta được: \(\widehat {{B_2}}\)= \(\widehat {{A_1}}\) b) Ta có: \(\widehat {{B_1}}\) và \(\widehat {{A_1}}\) là hai góc ở vị trí đồng vị. Đo góc ta được: \(\widehat {{B_1}}\)= \(\widehat {{A_1}}\) Luyện tập 2 1. Cho Hình 3.36, biết MN//BC, \(\widehat {ABC} = 60^\circ ,\widehat {MNC} = 150^\circ \). Hãy tính số đo các góc BMN và ACB. 2. Cho Hình 3.37, biết rằng xx’//yy’ và zz’ \( \bot \) xx’. Tính số đo góc ABy và cho biết zz’ có vuông góc với yy’ không Phương pháp giải: Sử dụng tính chất: Nếu 1 đường thẳng cắt hai đường thẳng song song thì: Hai góc so le trong bằng nhau Hai góc đồng vị bằng nhau Lời giải chi tiết: 1. Vì MN//BC nên \(\widehat {AMN} = \widehat {ABC}\)( 2 góc đồng vị), mà \(\widehat {ABC} = 60^\circ \)nên \(\widehat {AMN} = 60^\circ \) Vì \(\widehat {AMN} + \widehat {BMN} = 180^\circ \) (2 góc kề bù) \(\begin{array}{l} \Rightarrow 60^\circ + \widehat {BMN} = 180^\circ \\ \Rightarrow \widehat {BMN} = 180^\circ - 60^\circ = 120^\circ \end{array}\) Vì \(\widehat {ANM} + \widehat {MNC} = 180^\circ \)(2 góc kề bù) \(\begin{array}{l} \Rightarrow \widehat {ANM} + 150^\circ = 180^\circ \\ \Rightarrow \widehat {ANM} = 180^\circ - 150^\circ = 30^\circ \end{array}\) Vì MN//BC nên \(\widehat {ANM} = \widehat {ACB}\) ( 2 góc đồng vị), mà \(\widehat {ANM} = 30^\circ \)nên \(\widehat {ACB} = 30^\circ \). 2. Vì xx’//yy’ nên \(\widehat {x'AB} = \widehat {ABy}\)( 2 góc so le trong) Mà zz’\( \bot \) xx’ nên \(\widehat {x'AB} = 90^\circ \) Do đó, \(\widehat {ABy} = 90^\circ \) nên zz’ vuông góc với yy’.
|