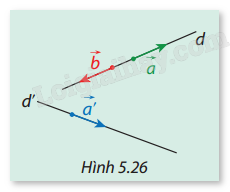
Giải mục 1 trang 67, 68 SGK Toán 12 tập 2 - Cùng khám pháCho hai vectơ ngược hướng (vec a) và (vec b) là hai vectơ chỉ phương của đường thẳng (d) và (vec a') là vectơ chỉ phương của đường thẳng (d')(Hình 5.26). Cho biết ((d,d') = {45^{^circ }}). Hãy tính số đo của hai góc: (left( {vec a,vec a'} right)) và ((vec b,vec a')). Từ đó chỉ ra mối quan hệ giữa hai góc ((d,d')) và ((vec a,vec a')), giữa (cos (d,d')) và (cos (vec a,vec a')).
Lựa chọn câu để xem lời giải nhanh hơn
HĐ1 Trả lời câu hỏi Hoạt động 1 trang 67 SGK Toán 12 Cùng khám phá Cho hai vectơ ngược hướng \(\vec a\) và \(\vec b\) là hai vectơ chỉ phương của đường thẳng \(d\) và \(\vec a'\) là vectơ chỉ phương của đường thẳng \(d'\)(Hình 5.26). Cho biết \((d,d') = {45^{^\circ }}\). Hãy tính số đo của hai góc: \(\left( {\vec a,\vec a'} \right)\) và \((\vec b,\vec a')\). Từ đó chỉ ra mối quan hệ giữa hai góc \((d,d')\) và \((\vec a,\vec a')\), giữa \(\cos (d,d')\) và \(\cos (\vec a,\vec a')\).
Phương pháp giải: Sử dụng tích vô hướng của hai vectơ để tính góc giữa chúng: \(\cos \theta = \frac{{\vec u \cdot \vec v}}{{|\vec u||\vec v|}}\) Lời giải chi tiết: - Góc giữa \(\vec a\) và \(\vec a'\): Ta sử dụng công thức cosin cho góc giữa hai vectơ: \(\cos (\vec a,\vec a') = \frac{{\vec a \cdot \vec a'}}{{\left| {\vec a} \right|.\left| {\vec a'} \right|}} = \frac{{{a_1}{{a'}_1} + {a_2}{{a'}_2} + {a_3}{{a'}_3}}}{{\sqrt {(a_1^2 + a_2^2 + a_3^2)({a_1}{'^2} + {a_2}{'^2} + {a_3}{'^2})} }}\) Biết rằng \((d,d') = {45^\circ }\) và Vì \(\overrightarrow a \) là vector chỉ phương của d và \(\overrightarrow {a'} \) là vector chỉ phương của d' nên góc giữa hai vector bằng góc giữa hai đường thẳng. Suy ra góc giữa \(\vec a\) và \(\vec a'\) là \({45^\circ }\). - Góc giữa \(\vec b\) và \(\vec a'\): Vì \(\vec b = - \vec a\), ta có: \(\cos \left( {\vec b,\vec a'} \right) = \cos \left( { - \vec a,\vec a'} \right) = - \cos \left( {\vec a,\vec a'} \right) = - \cos 45^\circ \) Suy ra: \(\cos \left( {\vec b,\vec a'} \right) = - \frac{1}{{\sqrt 2 }}\) Do đó, góc giữa \(\vec b\) và \(\vec a'\) là \({135^\circ }\). - Mối quan hệ giữa hai góc: Góc giữa hai đường thẳng \((d,d')\) và góc giữa hai vectơ chỉ phương \(\vec a\) và \(\vec a'\) bằng nhau, tức là: \((d,d') = \left( {\vec a,\vec a'} \right) = {45^\circ }\) - Tương tự, mối quan hệ giữa \(\cos (d,d')\) và \(\cos \left( {\vec a,\vec a'} \right)\) là: \(\cos (d,d') = \cos \left( {\vec a,\vec a'} \right) = \frac{1}{{\sqrt 2 }}\) LT1 Trả lời câu hỏi Luyện tập 1 trang 68 SGK Toán 12 Cùng khám phá Trong không gian Oxyz, tính góc giữa hai đường thẳng d và d' trong các trường hợp sau: a) \(d:\frac{x}{3} = \frac{y}{4} = \frac{z}{5}\) và \(d':\frac{{x - 1}}{4} = \frac{y}{2} = \frac{{z + 1}}{2}\) b) \(d:\frac{x}{2} = \frac{y}{{ - 4}} = \frac{z}{5}\) và \(d':\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x = 2 - t\;\\y = 3 + 2t\;\\z = 2t\end{array}\end{array}} \right.\) \((t \in \mathbb{R})\) Phương pháp giải: Xác định vector chỉ phương của mỗi đường thẳng. Sử dụng công thức cosin góc giữa hai vector: \(\cos (\vec a,\vec b) = \frac{{\vec a \cdot \vec b}}{{|\vec a||\vec b|}}\). Tính góc từ giá trị cosin. Lời giải chi tiết: a) Vector chỉ phương: \(d:\overrightarrow {{a_1}} = (3,4,5)\) \(d':\overrightarrow {{a_2}} = (4,2,2)\) Áp dụng công thức: \(\cos (\overrightarrow {{a_1}} ,\overrightarrow {{a_2}} ) = \frac{{3 \cdot 4 + 4 \cdot 2 + 5 \cdot 2}}{{\sqrt {({3^2} + {4^2} + {5^2})({4^2} + {2^2} + {2^2})} }}\) \( = \frac{{12 + 8 + 10}}{{\sqrt {(9 + 16 + 25)(16 + 4 + 4)} }}\) \( = \frac{{30}}{{\sqrt {50 \cdot 24} }}\) \( = \frac{3}{{\sqrt 2 }}\) Suy ra góc \(\phi = 30^\circ \) b) Vector chỉ phương: \(d:\overrightarrow {{a_1}} = (2, - 4,5)\) \(d':\overrightarrow {{a_2}} = ( - 1,2,2)\) Áp dụng công thức: \(\cos (\overrightarrow {{a_1}} ,\overrightarrow {{a_2}} ) = \frac{{2 \cdot ( - 1) + ( - 4) \cdot 2 + 5 \cdot 2}}{{\sqrt {({2^2} + {{( - 4)}^2} + {5^2})({{( - 1)}^2} + {2^2} + {2^2})} }}\) \( = \frac{{ - 2 - 8 + 10}}{{\sqrt {(4 + 16 + 25)(1 + 4 + 4)} }}\) \( = \frac{0}{{\sqrt {45 \cdot 9} }}\) \( = 0\) Do \(\cos (\phi ) = 0\), nên \(\phi = 90^\circ \)
|