Giải mục 1 trang 35, 36, 37 SGK Toán 9 tập 2 - Cùng khám pháVới các điểm trong Hình 7.12, bạn An cho rằng có thể vẽ một đường tròn đi qua cả bốn điểm A, B, C, D còn bạn Bình thì cho rằng có thể vẽ được một đường tròn đi qua cả bốn điểm A, B, C, E. Hãy vẽ đường tròn đi qua ba điểm A, B, C và cho biết bạn nào đúng. Tổng hợp Đề thi vào 10 có đáp án và lời giải Toán - Văn - Anh
Lựa chọn câu để xem lời giải nhanh hơn
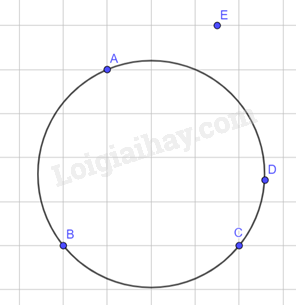
HĐ1 Trả lời câu hỏi Hoạt động 1 trang 35 SGK Toán 9 Cùng khám phá Với các điểm trong Hình 7.12, bạn An cho rằng có thể vẽ một đường tròn đi qua cả bốn điểm A, B, C, D còn bạn Bình thì cho rằng có thể vẽ được một đường tròn đi qua cả bốn điểm A, B, C, E. Hãy vẽ đường tròn đi qua ba điểm A, B, C và cho biết bạn nào đúng. Phương pháp giải: Dùng compa vẽ đường tròn đi qua 3 điểm A, B,C và kết luận. Lời giải chi tiết:
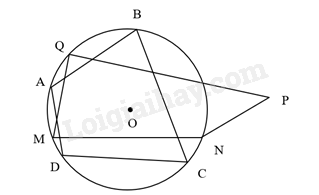
Theo hình vẽ bạn An đúng. LT1 Trả lời câu hỏi Luyện tập 1 trang 36 SGK Toán 9 Cùng khám phá Vẽ một tứ giác nội tiếp hình tròn và một tứ giác không nội tiếp đường tròn. Phương pháp giải: Dựa vào một tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp. Lời giải chi tiết:
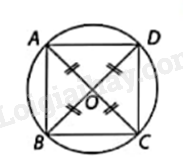
Trên hình vẽ tứ giác ABCD là tứ giác nội tiếp đường tròn, tứ giác MNPQ là tứ giác không nội tiếp đường tròn. HĐ2 Trả lời câu hỏi Hoạt động 2 trang 36 SGK Toán 9 Cùng khám phá Giải thích vì sao giao điểm của hai đường chéo của hình chữ nhật và hình vuông cách đều bốn đỉnh của chúng. Phương pháp giải: Trong hình chữ nhật, hình vuông ta có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường. Lời giải chi tiết: Theo tính chất của hình chữ nhật và hình vuông: Trong hình chữ nhật, hình vuông ta có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường nên giao điểm của hai đường chéo của hình chữ nhật và hình vuông cách đều bốn đỉnh của chúng. LT2 Trả lời câu hỏi Luyện tập 2 trang 37 SGK Toán 9 Cùng khám phá Xác định tâm và đường kính của đường tròn ngoại tiếp hình vuông có cạnh 3 cm. Phương pháp giải: Đường tròn ngoại tiếp hình vuông có tâm là giao điểm của hai đường chéo và bán kính là nửa đường chéo. Lời giải chi tiết:
Gọi O là giao điểm của hai đường chéo AC và BD. Khi đó, đường tròn ngoại tiếp hình vuông ABCD có tâm là O và bán kính bằng 12AC. Vì tam giác ABC vuông tại B nên AC = √AB2+BC2=√32+32=3√2 cm Do đó R = 12AC = 12. 3√2 = 3√22cm
|